ЗАТВЕДЖЕНО

Дата добавления: 2015-10-19; просмотров: 624

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

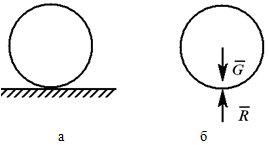
а – тело весом G на гладкой поверхности; б – действие поверхности заменено реакцией – силой R;

в – в точке А связь «опорная точка» или ребро; г – реакции направлены перпендикулярно

опираемой или опирающейся плоскостям

Рисунок 1.1

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).

а – балка висит на двух тросах; б – действие тросов заменено силами Т1 и Т2;

в – связь «идеальный стержень»; г – связь «идеальная нить»

Рисунок 1.2

Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, X_A и Y_A (рисунок 1.3, г).

Рисунок 1.3

Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

X_A= Rcosα; Y_A= Rsinα;

Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).

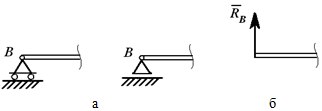
Рисунок 1.4

Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами X_A , Y_A и R_B .

Рисунок 1.5

Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы R_D и M_D момента.

Рисунок 1.6

На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент M_C (рисунок 1.7, б).

Рисунок 1.7

Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A ) и момент Μ_A (рисунок 1.8).

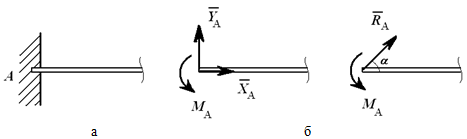
Рисунок 1.8

На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями. Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) X_A , Y_A и Z_A , т.е. силой, неизвестной по величине и направлению.

Рисунок 1.9

На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A , Y_A , Z_A и X_B , Z_B (рисунок 1.10, б).

Рисунок 1.10

На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.

Рисунок 1.11

Угол трения. Реакция идеально гладкой поверхности, как уже говорилось выше, направлена по нормали к поверхности. На шероховатой поверхности могут возникать силы трения скольжения. Поэтому реакцию шероховатой поверхности представим в виде двух составляющих: нормальной реакции N (равна по модулю силе нормального давления) и перпендикулярной ей силы трения F.

Полная реакция R=N + F всегда отклонена от нормали к поверхности на некоторый угол "альфа". На рисунке видно, что . Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу F1, мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения F = -F1, причем . С увеличением силы F1 будет возрастать и сила F . Наконец, при F1 = Fmax наступит предельное состояние равновесия, при котором полная реакция R отклонится от вертикали на угол "альфа"max, называемый углом трения. Обозначив его через "фи", получим .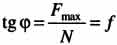

Тангенс угла трения равняется коэффициенту трения. Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения.

Трение скольжения.Возникновение трения скольжения обусловлено прежде всего шероховатостью поверхностей и наличием сцепления между телами. Изучение всех особенностей этого сложного физического явления выходит за рамки курса теоретической механики.

Трение скольжения в покое. В теоретической механике обычно исходят из ряда установленных экспериментально закономерностей, которые с достаточной для практики точностью описывают трение.

Коэффициент трения скольжения f также является безразмерной величиной и определяется опытным путем. Значение f зависит от материалов скользящих тел и оно меньше значения коэффициента трения покоя f₀. Последнее наблюдал каждый, кто передвигал тяжелые предметы, например, мебель. После начала движения требуются усилия значительно меньшие, чем для того, чтобы сдвинуть предмет с места.

Билет6.Центр тяжести. Центр параллельных сил. Центр тяжести твердого тела.

Центр тяжести– центр приложения равнодействующей сил тяготения (веса) системы тел или материального тела. При определении положения центра тяжести тела используются гипотезы:

1. Линии действия сил тяготения, приложенные к отдельным частицам тела, параллельны.

2. Ускорение свободного падения g = const (высота рассматриваемых тел много меньше радиуса Земли и изменением величины ускорения свободного падения по высоте тела можно пренебречь)

3. Рассматриваемые тела – однородные (нет включений материалов с другой плотностью) и сплошные (нет пустот).