Процедури контролю за доставкою суднових запасів

Дата добавления: 2015-10-19; просмотров: 530

Механической системой (МС) называют совокупность взаимодействующих МТ или тел. Материальное тело является МС составляющих его частиц. МС, движение точек которой не ограничено связями, называется системой свободных материальных точек. Внешними силами , k= 1,2 …,n называют силы, c которыми на точки системы действуют тела, не принадлежащие к этой системе. Внутренними силами называют силы , k= 1,2 …,m, c которыми взаимодействуют точки системы. Можно показать, главный вектор и главный момент системы системы внутренних сил равны нулю. Отсюда не вытекает, что внутренние силы уравновешиваются в общем случае, т.к. они могут вызывать перемещения точек системы (уравновешиваются в АТТ).

Массой системы называют сумму масс частиц системы

M=Σm_k.

Положение центра масс системы (т. С) определяется по формулам

,

.

Для тела имеем

,

.

В однородном поле силы тяжести центры масс и тяжести совпадают.

Моментами инерции МС относительно оси и точки называют величины

J_l=Σm_k∙h_k².

J_O=Σm_k∙r_k²

где h_k и r_k – расстояние точки тела с массой m_k от оси l иточки O.

Для твердого тела момент инерции относительно оси и точки

,

.

Моменты инерции относительно декартовых осей и начала координат

J_x=Σm_k∙(y_k²+z_k²), J_y=Σm_k∙(x_k²+z_k²), J_z=Σm_k∙( x_k²+y_k²),

J_O=Σm_k∙r_k²= Σm_k∙∙( x_k²+y_k²+z_k²),

Моменты инерции относительно координатных плоскостей равны

J_xy=Σm_k∙ z_k², J_yz=Σm_k∙x_k², J_xz=Σm_k∙y_k².

Имеются зависимости

2J_O= J_x+ J_y+ J_z,

J_O= J_xy+ J_yz+ J_xz.

Для тела моменты инерции определяются интегралами по массе

, , .

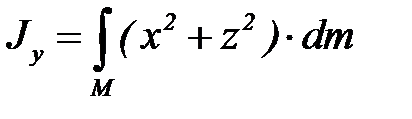Теорема Гюйгенса-Штейнера: момент инерции системы J_z относительно какой-либо оси z равен сумме момента инерции системы J_zC относительно параллельной ей оси z_C, проходящей через центр масс, и произведения массы системы M на квадрат расстояния между осями d

.

Среди семейства параллельных осей момент инерции относительно оси, проходящей через центр масс - наименьший.