
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Процедура контролю за суднами, що мають намір зайти до порту
Дата добавления: 2015-10-19; просмотров: 640
|
|
Здесь  и
и  определяют по их проекциям на оси естественного трехгранника Мtnb, имеющие начало в точке М и движущиеся вместе с нею (рисунок 3.5). Направления осей: Мt - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn - по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она
определяют по их проекциям на оси естественного трехгранника Мtnb, имеющие начало в точке М и движущиеся вместе с нею (рисунок 3.5). Направления осей: Мt - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn - по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она 
| Рисунок 3.5 |
Определим скорость точки
 .
.
Проекция скорости точки на касательную к ее траектории
 .
.
Очевидно, что  и модуль скорости
и модуль скорости  .
.
Для ускорения точки имеем

т.к.  (ρ – радиус кривизны траектории точки в рассматриваемом положении), то
(ρ – радиус кривизны траектории точки в рассматриваемом положении), то
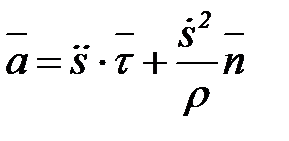 ,
,
т.е., ускорение равно сумме касательной и нормальной составляющих
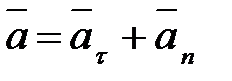 .
.
Вектор  лежит в соприкасающейся плоскости, т. е в плоскости Mtn. Проецируя обе части равенства на оси Мt, Мn и Mb, получим
лежит в соприкасающейся плоскости, т. е в плоскости Mtn. Проецируя обе части равенства на оси Мt, Мn и Mb, получим
 .
.
Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f''(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v2/R, где v – модуль скорости точки в данный момент; R – радиус кривизны траектории в месте, где находится точка в данный момент.

Билет10.Поступательное и вращательное движения твердого тела. Равномерное и равнопеременное вращения.
Поступательным называется такое движение АТТ, при котором любая прямая, проведенная в теле, перемещается, оставаясь параллельной себе, при этом траектории его точек могут быть любыми кривыми. Справедлива теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Кинематика АТТ в этом случае сводится к кинематике точки.
При вращении АТТ вокруг неподвижной оси, его точки, лежащие на оси, остаются неподвижными (АВ на рисунке 3.6). Через ось проведем две плоскости - неподвижную и подвижную, связанную с телом. Двугранный угол j между ними называют углом поворота тела и считают положительным, когда он отсчитывается от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Закон вращения АТТ вокруг неподвижной оси – это зависимость

| Рисунок 3.6 |
Угловая скорость характеризует изменение j
w = dj/dt или 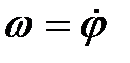 .
.
Угловое ускорение характеризует изменение  с течением времени
с течением времени
e = dw/dt = d2 j/dt2 или  .
.
Если во все время движения w=const, то вращение называют равномерным. Из формулы w = dj/dt интегрируя, найдем его закон  .
.
При равномерном вращении, если  , то
, то 
Если угловое ускорение тела во все время движения остается постоянным (e=const), то вращение называется равнопеременным, закон которого имеет вид
 .
.
Билет11.Скорости и ускорения точек вращающегося тела.
При вращении точка М описывает окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр P лежит на оси. За время dt тело поворачивается на угол dj, точка М совершает перемещение ds = h∙ dj. Тогда
 .
.
Ускорения точки найдем как
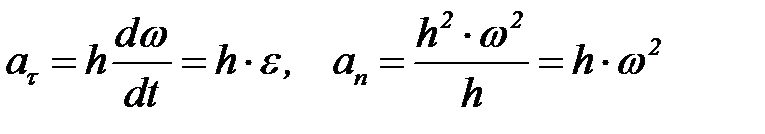 .
.
Ускорение  направлено по касательной к траектории (в сторону движения при ускоренном вращении и в обратную сторону при замедленном), ускорение
направлено по касательной к траектории (в сторону движения при ускоренном вращении и в обратную сторону при замедленном), ускорение  всегда направлено по радиусу МP к оси. Полное ускорение точки равно
всегда направлено по радиусу МP к оси. Полное ускорение точки равно
 ,
,
а угол m определяется через зависимость
 .
.
Для векторов  и
и  можно получить формулы
можно получить формулы
 ,
,
 .
.
Билет12.Уравнения плоскопараллельного движения. Определение скоростей точек плоской фигуры. Теорема о проекциях скоростей двух точек.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис. 1.56).

Рис. 1.56 Рис. 1.57
При плоскопараллельном движении все точки тела, лежащие на прямой 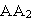 , перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как дви-жется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение.
, перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как дви-жется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение.
Положение сечения в плоскости OXY определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис. 1.57). Положение отрезка АВ можно определить, зная координаты  точки А и угол
точки А и угол  , который от-резок АВ образует с осью x.
, который от-резок АВ образует с осью x.
Точку А, выбранную для определения положения сечения, называют полюсом. При движении тела величины  и
и  будут меняться:
будут меняться:
 (1.74)
(1.74)
Уравнения (1.74), определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела.
Теорема 1. Абсолютная скорость 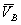 любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости
любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости  про-извольно выбранного полюса в поступательном движении плоской фигуры и вращательной скорости
про-извольно выбранного полюса в поступательном движении плоской фигуры и вращательной скорости  во вращательном движении фигуры относительно полюса.
во вращательном движении фигуры относительно полюса.
Положение любой точки В тела можно определить равенством

Взяв производную от обеих частей уравнения по времени получим,
 ,
,
где  - искомая скорость;
- искомая скорость;  - скорость полюса;
- скорость полюса;  - скорость точки В при вращательном движении тела вокруг полюса А при
- скорость точки В при вращательном движении тела вокруг полюса А при  Таким образом
Таким образом


Теорема 2. Проекции скоростей двух точек плоской фигуры на ось, про-ходящую через эти точки, равны и имеют одинаковый знак (рис. 1.60). Зная, что 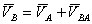 , спроецируем данное выражение на прямую АВ, тогда
, спроецируем данное выражение на прямую АВ, тогда

Известны направления скоростей двух точек. Рассмотрим этот случай на примере кривошипно-шатунного механизма (рис. 1.66). Направления скоростей точки А кривошипа и ползуна В известны. МЦС должен лежать в точке пересечения перпендикуля-ров к направлениям скоростей этих точек. Эта точка в бесконечности. Точка А принадлежит кривошипу и ее скорость  , но точка А также принадлежит и шатуну АВ. Выберем точку А за полюс, тогда
, но точка А также принадлежит и шатуну АВ. Выберем точку А за полюс, тогда 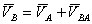 , спроецируем на прямую АВ:
, спроецируем на прямую АВ:
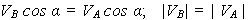
Спроецируем векторное равенство на перпендикуляр к АВ:

Шатун АВ совершает, так называемое, мгновенно-поступательное движение.
Билет13.Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Определение ускорений точек плоской фигуры.
| <== предыдущая лекция | | | следующая лекция ==> |
| Термін дії та достовірність Міжнародного свідоцтва | | | Процедура контролю за суднами під час їх перебування в ПЗ |