
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Термін дії та достовірність Міжнародного свідоцтва
Дата добавления: 2015-10-19; просмотров: 633
|
|
Движение точки может быть задано одним из трех способов.
1. Векторный способ. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение точки в любой момент времени можно определить, задав ее радиус-вектор  (рисунок 3.1) как функцию от времени t
(рисунок 3.1) как функцию от времени t
| Рисунок 3.1 |

 . (3.2.1)
. (3.2.1)
Это и есть закон движения точки в векторной форме.
2. Координатный способ. Положение точки можно непосредственно определять ее координатами, изменяющимися при движении с течением времени
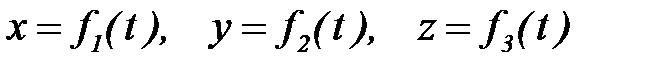 . (3.2.2)
. (3.2.2)
| Рисунок 3.2 |
 Это - закон движения точки в прямоугольных декартовых координатах.
Это - закон движения точки в прямоугольных декартовых координатах.
3. Естественный способ. Задать движение точки естественным способом – это задать (рисунок 3.2) ее траекторию, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде
 .
.
Скоростью точки в данный момент времени t называется величина  , так что скорость есть первая производная от вектора
, так что скорость есть первая производная от вектора  по аргументу t:
по аргументу t:
 .
.
Ускорением точки в данный момент времени t называют векторную величину, к которой стремится  при стремлении промежутка времени Dt к нулю
при стремлении промежутка времени Dt к нулю
 .
.
т.е., вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени
Билет8.Определение скорости и ускорения точки при координатном способе задания движения.
Используем следующую теорему: проекция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось.
Тогда для проекций скорости имеем

или  .
.
т.е., проекции скорости точки на координатные оси равны первым производным от проекций соответствующих координат точки по времени.
Для проекций ускорения имеем
 ,
,  ,
, 
или  , т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.
, т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.
Билет9.Оси естественного трехгранника. Числовое значение скорости. Касательное и нормальное ускорения точки.
| <== предыдущая лекция | | | следующая лекция ==> |
| ЗАТВЕДЖЕНО | | | Процедура контролю за суднами, що мають намір зайти до порту |