Тиристорный преобразователь при
мгновенной коммутации.
Как было показано, неуправляемый выпрямитель может обеспечить только одно значение ЭДС на выходе (ed0), т.е. максимально возможное в схеме. Для получения возможности регулирования величины ЭДС преобразователь выполняют управляемым, включая вместо неуправляемых вентилей, тиристоры. Естественно, при этом, необходимо организовать систему управления тиристорами, однако, на начальном этапе рассмотрения работы управляемого преобразователя, будем предполагать, что включение тиристоров, т.е. подачу на их управляющие электроды импульсов, мы можем обеспечить в любой, желательный для нас, момент времени.
Рис 14
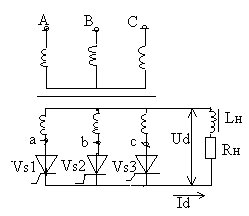
Если управляющие импульсы подавать на управляющие электроды тиристоров в моменты естественной коммутации, то получим также, как и при неуправляемых вентилях, максимально возможную ЭДС Ed0. Регулирование ЭДС в сторону ее снижения осуществляется за счет задержки включения тиристоров относительно момента естественной коммутации. Величину этой задержки характеризует угол управления тиристорами преобразователя, обозначаемый в литературе буквой a. Угол управления преобразователем (a) - это угол, выраженный в электрических градусах, отсчитываемый от точки естественной коммутации двух чередующихся фаз до момента включения тиристора последующей фазы. Пусть управляющий импульс на тиристор VS1 подан в момент Q = Q1. Обратим внимание на то, что к моменту подачи управляющего импульса на VS1 ток в фазе “С” протекает встречно с фазной ЭДС за счет энергии, накопленной в индуктивности нагрузки рабочим током. Подача управляющего импульса на VS1 включает его, а тиристор VS3 - выключается. Далее при Q = Q2 с тем же углом задержки (a) подается управляющий импульс на VS2 и ток с фазы “А” коммутируется на фазу “В” и т.д. На рис 14 показана форма ЭДС преобразователя. Ниже показаны токи, протекающие по фазным обмоткам трансформатора в предположении идеальной сглаженности тока Id и мгновенной коммутации фазных токов с предыдущей на последующую фазу. Анализ диаграммы напряжения показывает: а) При увеличении угла a, т.е. при большей задержке управляющих импульсов Ed преобразователя снижается. Величина этого снижения, определяемая вольт - секундной площадкой Sз, тем больше, чем больше угол a. б) ЭДС преобразователя при a > 30° содержит участки как положительных (S+), так и отрицательных (S-) значений вольт - секундных площадок. С увеличением угла a (S+) уменьшаются, а (S-) - увеличиваются. в) Импульсы фазных токов трансформатора, сохраняя прямоугольную форму, смещаются в сторону отставания на величину угла a по отношению к точке естественной коммутации.
3.2.2.1.Величина ЭДС тиристорного преобразователя.
Принцип, используемый при определении среднего значения ЭДС на выходе тиристорного преобразователя, тот же, что был использован при определении среднего значения ЭДС неуправляемого преобразователя. Заключается он в том, что определяется площадь, заключенная между кривой, отражающей функцию изменения фазной ЭДС, и осью абсцисс. Эта вольт - секундная площадь, с учетом ее знака, определяется в пределах интервала повторяемости, как определенный интеграл, нижний и верхний пределы которого соответствуют границам интервала повторяемости. Взяв отношение вычисленной площади к длине интервала повторяемости, вычисляется среднее значение ЭДС тиристорного преобразователя для интересующей нас величины Ð a.
=(mn /2p) eф.м.{cos{(p(mn -2)/2mn)+a }- cos {(p(mn +2)/2mn)+a }} = eф.м (mn /p) sin (p/mn) cos a = Ed0 cos a. Таким образом, выявлена очень простая зависимость, связывающая величину средней выпрямленной ЭДС на выходе тиристорного преобразователя Ed, величину максимально возможной ЭДС этого ТП и углом управления a: Ed = Ed0 * cos a. Ее графическое представление называют регулировочной характеристикой ТП. Она имеет вид:
Рис. 15 Иногда угол a на оси абсцисс откладывается иначе (как показано на втором графике).Иногда на оси абсцисс откладывается некоторая другая переменная, связанная с Ð a линейной, или нелинейной зависимостью. Этот вопрос будет рассмотрен при изложении систем управления ТП.
3.2.2.2. Коммутация токов в фазах питающего трансформатора ТП при переключении вентилей.
Ранее процесс перехода тока с одной фазы трансформатора на другую рассматривался, как мгновенный. Это было обусловлено принятыми допущениями. В реальных схемах из-за наличия в цепях переменного тока индуктивных сопротивлений, в частности, индуктивных сопротивлений обмоток трансформатора, процесс коммутации имеет определенную длительность. Индуктивные сопротивления обмоток трансформатора, обусловленные потоками рассеяния в магнитной системе, определяются из опыта короткого замыкания трансформатора, и в расчетах учитываются в виде общей индуктивности Ls, представляющей собой суммарную индуктивность рассеяния вторичной обмотки и, приведенную к ней, индуктивность первичной обмотки. Влияние на процесс коммутации активных сопротивлений обмоток трансформатора учитывать не будем из-за незначительности этого влияния. По-прежнему выпрямленный ток считаем идеально сглаженным (wLн = ¥). На рис 16 представлена эквивалентная схема трехфазного нулевого выпрямителя и диаграммы напряжений и токов, поясняющие процесс коммутации токов. Индуктивные сопротивления обмоток учтены введением в схему индуктивностей Ls. Предположим, что в проводящем состоянии находится вентиль VS1. В момент Q1 поступает включающий импульс на вентиль VS2. Поскольку потенциал анода вентиля в этот момент положителен относительно катода, вентиль включается.
Начиная с момента Q1 оба тиристора включены и две фазы (“а” и “b”) вторичной обмотки трансформатора оказываются замкнутыми через них накоротко. Под воздействием ЭДС обмоток этих фаз (eа и eb) в короткозамкнутой цепи (контура коммутации) появляется ток короткого замыкания ik, который является коммутирующим током. Этот ток можно в любой момент интервала коммутации (Q2 - Q1) определить по формуле: ik = (U2m/2Xs)*{cos a - cos (a + Q)} (3-7)
где U2m -амплитудное значение линейного напряжения между фазами “a” и “b”. Xs= wLS (3-8) a - угол управления. Нужно отметить, что через вентиль VS1 фазы “а” ток ik протекает в непроводящем направлении. Такое возможно, т.к. вентиль VS1 смещен прямым током Id, протекавшем через него до начала коммутации. Ток ik направлен от фазы “b” с большим потенциалом к фазе “а” с меньшим потенциалом. Учитывая, что выпрямленный ток Id при wLн = ¥ в интервале коммутации остается неизменным, можно, согласно первому закону Кирхгофа для точки 0 записать: ia + ib + Id = 0; или с учетом направления токов: ia + ib = Id = const. Последнее уравнение справедливо для любого момента интервала коммутации. Пока ток проводит только вентиль VS1, получаем ia = Id и ib = 0. На интервале одновременной проводимости вентилей VS1 и VS2 (интервал коммутации тока с фазы “а” на фазу “b”): ia = Id - ik и ib = ik. Когда коммутация закончится и ток будет проводить только вентиль VS2, получим: ib = Id; ia = 0. Из рис 16 видно, что в интервале от Q1 до Q2 ток ib плавно увеличивается, а ia уменьшается. Когда ток ib станет равным Id, а ток ia снизится до нуля, вентиль VS1 выключится и ток нагрузки будет продолжать протекать только через вентиль VS2. Длительность интервала коммутации характеризуется углом коммутации g, который может быть определен из следующего уравнения (для трехфазной нулевой и трехфазной мостовой схем):
обозначив угол коммутации g при угле управления a = 0 через g0, можно записать:
Подставляя в исходное уравнение значение g0, получаем:
g = arccos {cos a + cos g0 - 1} - a.
Согласно последней формуле с ростом угла a (в пределах 0< a < 90°) уменьшается угол коммутации g. Физическая сущность этого явления состоит в том, что с увеличением угла a (в указанных пределах) растет напряжение, под действием которого возрастает ток ik в контуре коммутации и, следовательно, до значения Id он нарастает быстрее. При дальнейшем росте угла a (90°< a< 180°) угол коммутации увеличивается. Процесс коммутации оказывает непосредственное влияние на выпрямленное напряжение Ud. Это связано с тем, что при изменении фазных токов в зоне коммутации в индуктивностях Ls обмоток трансформатора появляются ЭДС самоиндукции. В выходящей из работы фазе ЭДС самоиндукции складывается с ЭДС “ea”. Во вступающей в работу фазе ЭДС самоиндукции вычитается из “eb”. Таким образом, с учетом действия ЭДС самоиндукции мгновенное значение выпрямленного напряжения на интервале коммутации тока равно полусумме ЭДС коммутируемых фаз.
Ud = (Ua + Ub)/2. (3-12)
где Ua и Ub - мгновенные значения фазных напряжений вторичной обмотки трансформатора. Так как, в зоне коммутации мгновенное значение выпрямленного напряжения снижается, по сравнению с мгновенной коммутацией, до величины Ud, происходит уменьшение среднего значения выпрямленного напряжения. Его величина определяется выражением:
Из (3-7), (3-8), и (3-14) можно получить: Анализируя последнюю формулу, мы видим, что от двух первых множителей, стоящих в числителе, зависит ширина заштрихованной на диаграмме площадки. От значения третьего множителя (mn) зависит количество этих площадок, приходящихся на период переменного напряжения - (2p). В завершение рассмотрения процесса коммутации фазных токов обратим внимание на то, что коммутационное снижение средней величины выпрямленного напряжения не зависит от действующего значения переменного напряжения на вторичных обмотках питающего трансформатора, а, также, от величины угла управления “a”. Оно зависит только от трех величин, входящих в формулу (3-15).
|


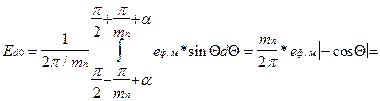




 (3-14)
(3-14)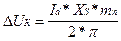 (3-15)
(3-15)


