Движение по окружности. Движение тела по окружности является частным случаем криволинейного движения
Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения
При малых углах поворота Δ l ≈ Δ s.
Угловой скоростью ω тел в данной точке круговой траектории называют предел (при Δ t → 0) отношения малого углового перемещения Δ φ к малому промежутку времени Δ t:
Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора Равномерное движение тела по окружности является движением с ускорением. Ускорение
направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
Для доказательства этого выражения рассмотрим изменение вектора скорости
Векторы скоростей Из подобия треугольников OAB и BCD (рис. 1.6.2) следует:
При малых значениях угла Δ φ = ω Δ t расстояние | AB | =Δ s ≈ υ Δ t. Так как | OA | = R и | CD | = Δ υ, из подобия треугольников на рис. 1.6.2 получаем:
При малых углах Δ φ направление вектора
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным. В векторной форме центростремительное ускорение может быть записано в виде
где Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см. §1.1):
В этой формуле Δ υ τ = υ 2 – υ 1 – изменение модуля скорости за промежуток времени Δ t. Направление вектора полного ускорения
Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υ x и υ y (рис. 1.6.4). При равномерном вращении тела величины x, y, υ x, υ y будут периодически изменяться во времени по гармоническому закону с периодом
Глава 1. Механика
|

 удобно рассматривать угловое перемещение Δ φ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением
удобно рассматривать угловое перемещение Δ φ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением
 перемещения при движении тела по окружности.
перемещения при движении тела по окружности.

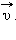


 за малый промежуток времени Δ t. По определению ускорения
за малый промежуток времени Δ t. По определению ускорения
 и
и 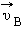 в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A = υ B = υ.
в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A = υ B = υ.

 при равномерном движении по окружности.
при равномерном движении по окружности.



 – радиус-вектор точки на окружности, начало которого находится в ее центре.
– радиус-вектор точки на окружности, начало которого находится в ее центре.
 определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
 при неравномерном движении тела по окружности.
при неравномерном движении тела по окружности.


 по координатным осям.
по координатным осям.



