оптимальным; 2) помехоустойчивым; 3) корректирующим
30. При передаче независимых сообщений источника по двоичному каналу процесс кодирования заключается в преобразовании сообщений в двоичные кодовые комбинации. При однозначном соответствии сообщений источника комбинациям кода энтропии кодовых комбинаций H(u) ___ энтропии источника H(a): 1) H(u) > H(a); 2) H(u) = H(a); 3) H(u) < H(a). 31. Основные принципы оптимального кодирования состоят в том, чтобы так закодировать сообщение, чтобы скорость передачи достигла пропускной способности двоичного канала. Это выполняется, если число элементов в комбинации
(где Определить 1) 6; 2) 16; 3) 4.
32. Код Шеннона-Фано удовлетворяет условию оптимального кодирования
(где
33. Алгоритм оптимального табличного построения кода Шеннона-Фано: « Знаки алфавита сообщений выписывают в таблицу в порядке убывания вероятностей. Затем их разделяют на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем знакам верхней половины в качестве первого символа приписывают – 0, а всем нижним – 1. Каждую из полученных групп, в свою очередь, разбивают на две подгруппы с одинаковыми суммарными вероятностями и так далее. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одному знаку. Проведите эффективное (оптимальное) табличное кодирование для алфавита
1) 1; 2) 2; 3) 3. 34. Когда методика Шеннона-Фано неоднозначна при построении эффективного кода, путем разбиения на подгруппы по суммарной вероятности верхней 1) 35. Методика Хаффмена гарантирует однозначное построение оптимального кода, путем циклического объединения двух букв с меньшими вероятностями в одну с вероятностью равной сумме двух и так далее, пока не получится алфавит с одной буквой с вероятностью равной единице. При алфавите из четырех букв
1) 1; 2) 2; 3) 3.
ЛИТЕРАТУРА: 1. Дмитриев В.И. Прикладная теория информации. – М.: «Высш. шк.», 1989 – 320 с.: ил. 2. Куликовский Л.Ф., Мотов В.В. Теоретические основы информационных процессов – М.: «Высш. шк.», 1987 – 248с. 3. Зюко А.Г., Коробов Ю.Ф. Теория передачи сигналов. – М.: «Связь», 1972 – 282 с.: ил. 4. Кловский Д.Д. Теория передачи сигналов. – М.: «Связь», 1973 – 376 с.: ил. 5. Назаров М.В. и другие. Теория передачи сигналов. – М.: «Связь», 1970 – 368с.: ил. 6. Липкин И.А. Основы статистической радиотехники, теории информации и кодирования. – М.: «Сов. радио», 1978 – 240с.: ил. 7. Яглом А.М., Яглом И.М. Вероятность и информация. – М.: «Наука», 1973 – 512с.: ил. 8. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах – М.: «Связь», 1978 – 252с.: ил. 9. Кловский Д.Д., Шилкин В.А. Теория электрической связи – М.: «Радио и связь», 1990 – 280с.: ил. 10. Горяинов В.Т., Журавлев А.Г., Тихонов В.И. Статистическая радиотехника. Примеры и задачи. – М.: «Сов. радио», 1980 – 544с.: ил. 11. Кузнецов О.Г. и др. Дискретная математика для инженера. – М.: «Энергия», 1980 – 344с.: ил. 12. Самсонов Б.Б. и др. Теория информации и кодирования. – Ростов на Дону.: «Феникс», 2002 – 288с. (Математические основы). 13. Электросвязь 2003, №1 «Электронная Россия» в 2002 и 2003 годах. - 10÷ 11с. 14. Липкин И.А. Статистическая радиотехника. Теория информации и кодирования. – М.: «Вузовская книга», 2002. – 216с.: ил. 15. Макаров А.А., Чиненков Л.Л. Основы теории передачи информации. Учебное пособие – М.: «СибГУТИ», 1998. – 39с.: ил.
16. Теория электрической связи. Учебник для вузов. Под ред. Д.Д. Кловского. – М.: «Радио и связь», 1998. – 432с.: 204ил.
Содержание Предисловие 2 Введение 3 1. концепцтуальные основы информационных процессов 4 О понятии «Информация» 4 Виды и свойства информации 5 Этапы обращения информации 6 Информационные системы 7 Система передачи информации 8 Уровни проблем передачи информации 11 О смысле «Теория информации» в системе связи 12 Контрольные вопросы к разделу 1 в форме «задание-тест» 13 2. Математические основы теории вероятностей 15 2.1 случайное событие и вероятность 15 2.2 Случайные величины и их вероятностные характеристики 19 2.3 Случайные функции и их вероятностное описание 25 2.4 Корреляционные характеристики случайных процессов 25 2.5 Контрольные вопросы к разделу 2 в форме «задание-тест» 29 3. КОличественная оценка информации 33 3.1 энтропия, как мера неопределенности выбора независимых сообщений дискретного источника 33 3.2 Свойства энтропии 36 3.3 Условная энтропия и ее свойства 39 3.4 Энтропия непрерывного источника информации (дифференциальная энтропия) 44 3.5 Передача информации от дискретного источника 49 3.6 Передача информации от непрерывного источника 52 3.7 Основные свойства количества информации 52 4. информационные характеристики источника сообщений и канала связи 53 4.1 Введение 53 4.2 Информационные характеристики источника дискретных сообщений 54 4.2.1. Модели источника дискретных сообщений 54 4.2.2. Свойства эргодических последовательностей знаков 55 4.2.3. Избыточность источника 57 4.2.4. Производительность источника дискретных сообщений 58 4.3 Информационные характеристики дискретных каналов связи 59 4.3.1 Модели дискретных каналов 59 4.3.2 Скорость передачи информации по дискретному каналу 61 4.3.3 Пропускная способность дискретного канала без помех 62 4.3.4 Пропускная способность дискретного канала с помехами 63 4.3.5 Информационные характеристики непрерывных каналов связи 66 4.4 Согласование физических характеристик сигнала и канала 70 4.5 Согласование статистических свойств источника сообщений и канала связи 71 4.6 Контрольные вопросы к разделам 3 и4 в форме «задание-тест» 73 5. основы теории оптимального кодирования 79 5.1 Кодирование как процесс выражения информации в цифровом виде 79 5.2 Классификация кодов 83 5.3 Представление кодов 84 5.4 Оптимальное (эффективное) статистическое кодирование 86 5.4.1 Методы эффективного кодирования некоррелированной последовательности знаков 88 5.4.2 Свойства префиксности эффективных кодов 94 5.4.3 Методы эффективного кодирования коррелированной последовательности знаков 95 5.4.4 Недостатки системы эффективного кодирования 96 5.5 Контрольные вопросы к разделу 5 в форме «задание-тест» 96 литература 105 содержание 106
|

 определяется как:
определяется как:
 − априорная вероятность
− априорная вероятность  -го сообщения).
-го сообщения). )
)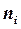 − число элементов в двоичной комбинации,
− число элементов в двоичной комбинации,  − априорная вероятность
− априорная вероятность  -го сообщения). Определите
-го сообщения). Определите 



 с вероятностями
с вероятностями 
 группы и вероятности нижней
группы и вероятности нижней  группы:
группы:



