Бод; 2) бит (двоичная цифра); 3) байт3. Неопределенность источника, приходящаяся на одно сообщение определяется по формуле Хартли:
(где p(xi) – вероятность появления xi -го сообщения) при p(xi)= 1) 8; 2) 3; 3) 4. 4. Энтропия H(x) как средняя мера неопределенности, приходящаяся на одно неравновероятное сообщение (независимые и несовместные) источника в соответствии с правилами теории вероятности определяется по формуле (p(xi) – вероятности появления i-го сообщения источника): 1)
5. Энтропия ансамбля двух сообщений x1 и x2 (с априорной вероятностью p(x1) = p и p(x2) = 1 – p(x1) = 1 – p) определяемая по формуле: 1) 0; 2) 1; 3) 6. Энтропия источника равновероятных сообщений H0(x)=logM=-logp(x) и неравновероятных сообщений 1) H0(x) = H i(x); 2) H0(x) < H i(x); 3) H0(x) > H i(x).
7. Энтропия двоичного источника с независимым выбором элементов, определяемой по формуле: H(x) = -plog2p - (1-p)log2(1-p) (здесь p – вероятность выбора одного элемента), при p = 1)
8. Энтропия (если вероятность одного из состояний источника сообщений равна единица) равна бит: 1) 0; 2)1; 3) 9. Энтропия объединения нескольких статистически независимых источников информации определяется как ________ энтропий источников:
|
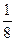равна бит:
; 2) 
; 3) 
.
достигает максимального значения H(x) = 1 бит при априорной вероятности p равной:
.
(p(xi) – вероятности появления i-го сообщения) между собой находится:
; 2) 1; 3) 
.
