Если частный характер количества информации специально не оговаривается, мы всегда имеем дело с количеством информации, приходящимся в среднем на один элемент сообщения
3.6 Передача информации от непрерывного источника [1 и др.]. Количество информации, получаемой от непрерывного источника по каналу с помехами, определяется так же, как в случае, рассмотренном выше, но с использованием понятия дифференциальной энтропии. Для источника, имеющего непрерывное множество состояний, среднее количество информации, содержащееся в каждом принятом значении случайной величины S относительно переданного значения случайной величины Z, можно получить как разность априорной и апостериорной дифференциальных энтропий:
Соотношение (3.39) несложно выразить в виде, подобном (3.38):
Относительность дифференциальных энтропий в этом случае не принимается во внимание, поскольку количество информации не зависит от выбранного стандарта сравнения.
3.7 Основные свойства количества информации [1 и др.]. 1. Несмотря на то что частное количество информации может быть величиной отрицательной, количество информации неотрицательно. Действительно, согласно выражению
Тогда
2. При отсутствии статистической связи между случайными величинами Z и S
следовательно, в этом случае
(принятые элементы сообщения не несут никакой информации относительно переданных). 3. Количество информации в S относительно Z равно количеству информации в Z относительно S. Для доказательства этого утверждения воспользуемся выражением
Аналогично можно записать
Так как H(Z, S)=H(S, Z), то
откуда
4. При взаимно однозначном соответствии между множествами передаваемых и принимаемых элементов сообщений, что имеет место в отсутствии помехи, апостериорная энтропия равна нулю и количество информации численно совпадает с энтропией источника:
|

 (3.39)
(3.39)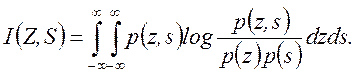 (3.40)
(3.40) (3.41)
(3.41)
 (3.42)
(3.42)



 (3.43)
(3.43) (3.44)
(3.44)


