Информационные характеристики источника дискретных сообщений
4.2.1 Модели источника дискретных сообщений [1 и др.]. В разделе 3 речь шла о средней неопределенности и среднем количестве информации, приходящимся на одно состояние источника сообщений. Математической моделью множества возможных реализаций источника была дискретная или непрерывная случайная величина. На практике, однако, нас чаще всего интересует не одно конкретное состояние источника, а дискретные или непрерывные последовательности состояний, реализуемых источником за длительный промежуток времени, например телеграммы, видеосюжеты и т.п. Для описания таких сообщений используются математические модели в виде дискретных и непрерывных случайных процессов. Для построения модели дискретных сообщений необходимо знать объем l алфавита знаков (z1, z2, …, z l), из которых источником формируется сообщения, и вероятности создания им отдельных знаков с учетом возможной взаимосвязи между ними. При доказательстве основных положений теории информации Шенноном использовалась модель, называемая эргодическим источником сообщений. Предполагается, что создаваемые им сообщения математически можно представить в виде эргодической случайной последовательности. Такая последовательность, как известно, удовлетворяет условиям стационарности и эргодичности. Первое означает, что вероятности отдельных знаков и их сочетаний не зависят от расположения последних по длине сообщения. Из второго следует, что статистические закономерности, полученные при исследовании одного достаточно длинного сообщения с вероятностью, близкой к единице, справедливы для всех сообщений, создаваемых источником. Из статистических характеристик в данном случае нас интересует средняя неопределенность в расчете на один знак последовательности. Стационарный источник сообщений, выбирающий каждый знак формируемой последовательности независимо от других знаков, всегда является эргодическим. Его также называют источником без памяти. На практике, однако, чаще встречаются источники, у которых вероятности выбора одного знака сообщения зависит от того, какие знаки были до этого (источники с памятью). Поскольку такая связь, как правило, распространяется на ограниченное число предыдущих знаков, для описания функционирования источника целесообразно использовать цепи Маркова. В Марковском эргодическом источнике вероятность передачи того или иного сообщения однозначно определяется состоянием источника. После передачи сообщения источник переходит в новое состояние, которое зависит от предыдущего состояния и переданного сообщения. Цепь Маркова порядка n характеризует последовательность событий, вероятности которых зависят от того, какие n событий предшествовали данному. Эти n конкретных событий определяют состояние источника, в котором он находится при выдаче очередного знака. Когда корреляционные связи наблюдаются только между двумя знаками (простая цепь Маркова), максимальное число различных состояний источника равно При наличии корреляционной связи между тремя знаками состояния источника определяется двумя предшествующими знаками и т.д. Аналитически можно получить выражения для энтропии источника сообщений при любой протяженности корреляционной связи.
4.2.2 Свойства эргодических последовательностей знаков [1 и др.]. Характер последовательностей, формируемых реальным источником сообщений, зависит от существующих ограничений на выбор знаков. Они выражаются в том, что вероятности реализации знаков различны и между ними существуют корреляционные связи. Эти ограничения приводят к тому, что вероятности формируемых последовательностей существенно различаются. Пусть, например, эргодический источник без памяти последовательно выдает знаки z1, z2, z3 в соответствии с вероятностями 0, 1; 0, 3; 0, 6. Тогда в образованной им достаточно длинной последовательности знаков мы ожидаем встретить в среднем на один знак z1 три знака z2 и шесть знаков z3. Однако при ограниченном числе знаков в последовательности существуют вероятности того, что она будет содержать; только знаки z1 (либо z2, либо z3); только знаки z1 и один знак z2 или z3; только знаки z2 и один знак z1 или z3; только знаки z3 и один знак z1 или z2; только знаки z1 и два знака z2 или z3 и т.д. С увеличением числа знаков вероятности появления таких последовательностей уменьшается. Фундаментальные свойства длинных последовательностей знаков, создаваемых эргодическим источником сообщений, отражает следующая теорема: как бы ни малы были два числа δ > 0 и μ > 0 при достаточно большом N, все последовательности могут быть разбиты на две группы. Одну группу составляет подавляющее большинство последовательностей, каждая из которых имеет настолько ничтожную вероятность, что даже суммарная вероятность таких последовательностей очень мала и при достаточно большом N будет меньше сколь угодно малого числа δ;. Эти последовательности называют нетипичными. Вторая группа включает типичные последовательности, которые при достаточно большом N отличаются тем, что вероятности их появления практически одинаковы, причем вероятность p любой такой последовательности удовлетворяет неравенству
где H(Z) – энтропия источника сообщений. Соотношение (4.1) называют также свойством асимптотической равномерности длинных последовательностей. Рассмотрим его подробнее. Поскольку при N→ ∞ источник сообщений с вероятностью, сколь угодно близкой к единице, выдает только типичные последовательности, принимаемое во внимание число последовательностей равно 1/р. Неопределенность создания каждой такой последовательности с учетом их равновероятности составляет log(1/p). Тогда величина log(1/p)/N представляет собой неопределенность, приходящуюся в среднем на один знак. Конечно, эта величина практически не должна отличатся от энтропии источника, что и констатируется соотношением (4.1). Приведем доказательство теоремы для простейшего случая эргодического источника без памяти. Оно непосредственно вытекает из закона больших чисел, в соответствии с которым в длинной последовательности из N элементов l (z1, z2, …, z l), имеющих вероятности появления p1, p2, …, p l содержится Np1 элементов z1, Np2 элементов z2 и т.д. Тогда вероятность p реализации любой типичной последовательности близка к величине
Логарифмируя правую и левую части выражения (4.2), получаем
откуда (при очень больших N)
Для общего случая теорема доказывается с привлечением цепей Маркова.
4.2.3 Избыточность источника [1 и др.]. Избыточность определяет насколько хорошо в источнике сообщений используются возможные элементы сообщения. Наиболее экономным является алфавит, использующий некоррелированные равновероятные символы. При наличии корреляционных связей между буквами (знаками) алфавита часть информации не является для получателя непредвиденной. Эту информацию можно не передавать по каналу связи, она может быть восстановлена на приемном конце на основании статистических характеристик алфавита. Мерой избыточности служит величина D, показывающая, насколько хорошо используются знаки данного алфавита источника:
где Hmax(Z) – максимально возможная энтропия, равная log l; H(Z) – энтропия источника. Если избыточность источника равна нулю, то формируемые им сообщения оптимальны в смысле наибольшего количества переносимой информации. Для передачи определенного количества информации I при отсутствии помех в этом случае необходимо k1=I/[Hmax(Z)] знаков. Поскольку энтропия сообщений, формируемых реальным источником, обладающим избыточностью, меньше максимальной, то для передачи того же количества информации I знаков требуется больше, а именно: k2=I/[H(Z)]> k1. Поэтому говорят также об избыточности знаков в сообщении или просто об избыточности сообщения, характеризуя ее тем же параметром D:
Избыточность нельзя рассматривать как признак несовершенства источника сообщений. Обычно она является следствием его физических свойств. Ограничения, существующие в любом естественном языке, связаны, например, с особенностями артикуляции, не позволяющими формировать слова, состоящие из произвольных сочетаний букв. Последствия от наличия избыточности сообщений неоднозначны. С одной стороны, избыточные сообщения требуют дополнительных затрат на передачу, например, увеличения длительности передач или расширения практической ширины спектра канала связи, что нежелательно. С другой стороны, при использовании сообщений, подчиняющихся априорно известным ограничениям, появляется возможность обнаружения и исправления ошибок, которые приводят к нарушению этих ограничений. Следовательно, наличие избыточности способствует повышению помехоустойчивости сообщений. Высокая избыточность большинства естественных языков обеспечивает, например, надежное общение людей даже при наличии у них акцентов и дефектов речи. Однако при обмене информацией в автоматических системах естественная избыточность подлежит устранению. Это объясняется тем, что алгоритмы обнаружения и исправления ошибок, базирующихся на статистических закономерностях функционирования источника, оказываются слишком сложными для реализации их техническими средствами. В случае необходимости для повышения помехоустойчивости затем вводится «рациональная» избыточность, позволяющая обеспечить обнаружение и исправление наиболее вероятных ошибок простыми техническими средствами. При низком уровне помех в канале связи устранение избыточности приводит к увеличению скорости передачи информации и может дать значительный экономический эффект. Пример 4.3. Определить возможный эффект от устранения избыточности при передачи текста на русском языке. Максимальная энтропия текста на русском языке (с учетом пренебрежения при передаче различиями в буквах е и ё, ъ и ь) установлена ранее (см. пример 3.1) и равна 5 дв. ед. Там же определена энтропия с учетом неравномерного распределения вероятностей появления отдельных букв (4.35 дв. ед). Имея сведения о переходных вероятностях и исходя из предположения, что текст представляет собой простую цепь Маркова, можно установить, что энтропия уменьшается до 3.52 дв. ед. Учет всех ограничений в языке, включая связи между словами, позволяет оценить минимальную величину энтропии значением 1, 5 дв. ед. Таким образом, избыточность русского языка составляет
Это означает, что каналы связи, построенные без учета ограничений, существующих в языке, и способных передавать равновероятные буквы, следующие друг за другом в любых сочетаниях, при передаче информации без помех текстом на русском языке используется всего на 30%. Полное устранение избыточности позволило бы повысить эффективности их использования более чем в 3 раза!
4.2.4 Производительность источника дискретных сообщений [1 и др.]. Под производительностью источника сообщений подразумевают количество информации, вырабатываемое источником в единицу времени. Эту характеристику источника называют также скоростью создания сообщений или потоком входной информации. Поскольку возможное воздействие помех на источник сообщений принято учитывать эквивалентным изменением характеристик модели канала связи, то производительность источника сообщений равна энтропии источника, приходящейся на единицу времени. Длительность выдачи знаков источником в каждом из состояний в общем случае может быть различной. Обозначим длительность выдачи знака zi, формируемого источником в состоянии Sq, через τ qzi. Тогда средняя длительность выдачи источником одного знака
Производительность источника Rи(z) теперь можно выразить формулой
Как следует из (4.5), повышение производительности источника возможно не только за счет увеличения энтропии, но и за счет снижения средней длительности формирования знака. Длительность знаков желательно выбирать обратно пропорциональными вероятностям их появления. Если длительность выдачи знака не зависит от состояния источника, для всех знаков одинакова и равна τ;, то τ и=τ;. Выражение для Rи(z) принимает вид
|

 (4.1)
(4.1) (4.2)
(4.2)
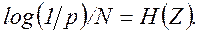 (4.3)
(4.3) (4.4)
(4.4)
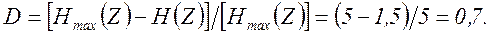
 (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7)


