Стабилизация температуры
Стабилизация температуры моделируемой системы в принципе может быть необходима по двум причинам: · образование дефектов кристаллической решётки, суперионный переход и плавление требуют энергии, так что в изолированной системе происходит повышение потенциальной энергии за счёт понижения температуры; поэтому, для моделирования кристаллов с постоянной температурой необходим алгоритм стабилизации температуры, моделирующий взаимодействие с термостатом; · опыт показывает, что накопление вычислительной погрешности приводит к медленному, но существенному при больших временах моделирования разогреву кристаллитов; для предотвращения разогрева тоже необходима стабилизация температуры. Идея стабилизации состоит в том, что в уравнения движения изолированной системы добавляется дополнительное слагаемое, понижающее скорости частиц в случае, если температура системы превосходит заданную и увеличивающее скорости в противоположном случае. Модификация скоростей производится умножением импульсов на коэффициент p x/ Q, одинаковый для всех частиц, так что она не приводит к возникновению движения или вращения системы как целого. Применение стабилизирующей температуру поправки в форме - было предложено Рябовым. Из его работ следует, что в форме - уравнения движения системы соответствуют гамильтониану, совпадающему с выражением для энтальпии H, так что они физически корректно описывают кристаллиты при нулевом (пренебрежимо малом) внешнем давлении и постоянной температуре. Таким образом, для термостатирования системы с нулевыми граничными условиями можно использовать следующие уравнения движения молекул:
Здесь N – количество частиц в системе; T – требуемая температура; p x - дополнительная переменная размерности Дж× с, связанная с термостатом, Q – величина размерности Дж× с2, задающая частоту колебаний температуры; индекс x не имеет самостоятельного значения, он только показывает, что p x - переменная, относящаяся к стабилизации температуры. В начале моделирования можно принять, что p x = 0. На последующих шагах моделирования эта величина изменяется по формуле
Значение константы Q в принципе произвольно, однако этим значением определяются период и амплитуда колебаний задаваемой температуры. Оценить необходимое значение Q можно из следующих соображений. Из-за слагаемого, соответствующего термостату, к скоростям частиц добавляется поправка
Если домножить обе части уравнения на
где E – удвоенная кинетическая энергия системы. Её требуемое значение как раз и равно 3 NkT. Учтём то, что
и то, что, в соответствии с формулами и,
Таким образом, временная зависимость отклонения величины E от 3 NkT даётся уравнением
Можно переписать уравнение в приближённой форме, считая, что E» 3 NkT; это верно, если температура колеблется не сильно. Кроме того, вводим новую переменную
причём
Теперь, дифференцируя обе части уравнения по времени, в приближении E» 3 NkT получаем
Это – уравнение гармонических колебаний с циклической частотой
откуда
где t - период колебаний. Выражение позволяет выбирать значение Q, исходя из требований, предъявляемых к периоду колебаний. Например так, чтобы период колебаний был существенно меньшим, чем время моделирования.
|

 ;
; ;
;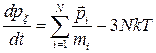 .
. .
. .
. и просуммировать по всем i, то получится, что
и просуммировать по всем i, то получится, что ,
,
 .
. .
. ,
, .
. .
. ,
, ,
,


