Компенсация импульса и момента импульса
Импульс модельного кристалла из N частиц даётся формулой
где m i – массы частиц,
Вычитание этой скорости из скоростей всех частиц останавливает собственное движение кристалла:
Предположим, что кристалл только вращается как твердое тело вокруг какой-нибудь оси, и больше частицы никуда не движутся (для упрощения выражений). Это вращение характеризуется постоянной угловой скоростью
Здесь
где N – количество частиц. Двойное векторное произведение можно преобразовать по формуле
тогда получится, что
Это векторное уравнение эквивалентно системе из трех уравнений для компонент векторов
Значения компонент векторов с верхними и нижними индексами одинаковы – положение индексов указывает на ко- и контравариантность векторов. Отметим также, что слагаемые вида
для симметричного относительно оси вращения кристалла равны нулю, так что и для реальных кристаллов должны быть близки к нулю. Таким образом, если для кристалла с произвольными скоростями частиц рассчитан момент импульса
то момент импульса кристалла станет равным нулю. При этом изменение самого импульса будет иметь вид
где M – масса кристалла,
|

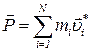 ,
,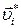 - их скорости до компенсации импульса. Скорость центра инерции кристалла связана с импульсом соотношением
- их скорости до компенсации импульса. Скорость центра инерции кристалла связана с импульсом соотношением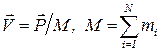 .
.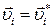 .
.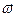 , связанной со скоростями частиц соотношением
, связанной со скоростями частиц соотношением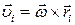 .
. - скорости и координаты i -ой частицы. Момент импульса этого кристалла рассчитывается по формуле
- скорости и координаты i -ой частицы. Момент импульса этого кристалла рассчитывается по формуле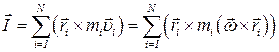 ,
,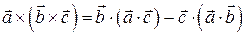 ,
, .
. и
и 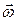 :
: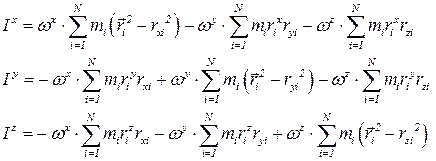 .
.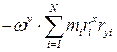
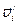 по формуле
по формуле ,
,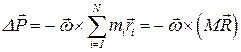 ,
,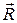 - радиус-вектор центра инерции. Очевидно, что если отсчитывать координаты
- радиус-вектор центра инерции. Очевидно, что если отсчитывать координаты  от центра инерции, то
от центра инерции, то 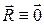 , и импульс не изменится. Кроме того, перед остановкой вращения кристалла нужно обнулить суммарный импульс, тогда ось вращения обязательно будет проходить через центр инерции, что подразумевается в формуле.
, и импульс не изменится. Кроме того, перед остановкой вращения кристалла нужно обнулить суммарный импульс, тогда ось вращения обязательно будет проходить через центр инерции, что подразумевается в формуле.


