Принципы моделирования ионных кристаллов методом молекулярной динамики
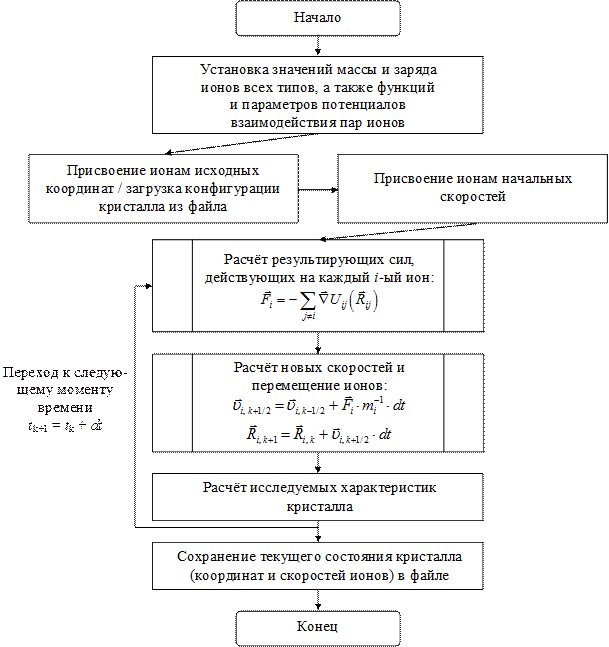
Простейший алгоритм программы, реализующей моделирование ионных кристаллов (или других физических систем) методом молекулярной динамики, может быть представлен в форме, показанной на рис. 6.1.
Рис. 6.1. Блок-схема алгоритма молекулярной динамики Заключается этот алгоритм в том, кристалл представляется системой недеформируемых, положительных и отрицательных, ионов, эволюционирующей во времени. Ионы перемещаются по законам Ньютона, а силы взаимодействия определяются парными потенциалами Uij (Rij). Потенциалы Uij (Rij) имеют общий вид
где Qi, Qi, - заряды i -го и j -го ионов, R ij – расстояние между этими ионами, K E – константа закона Кулона, Потенциалы
и потенциал Леннарда-Джонса
В формуле А и В – константы, характеризующие отталкивание оболочек, С 6, С 8 – константы, описывающие дипольную и квадрупольную составляющие дисперсионного притяжения. В формуле e - глубина минимума потенциала, а s - положение его нуля. Перед началом расчёта ионам присваиваются некоторые начальные координаты и скорости (например - координаты, соответствующие узлам идеальной кристаллической решётки моделируемого соединения и скорости, соответствующие Максвелловскому распределению при заданной температуре), после чего начинается численное пошаговое интегрирование уравнений движения ионов во времени. На каждом k -ом шаге производятся следующие действия: · Рассчитываются действующие на каждый ион силы
· Вычисляются новые скорости и новые координаты ионов
Формулы - справедливы при нулевых граничных условиях (конечный кристаллит из N частиц в вакууме) без компенсации перемещения, вращения и дрейфа температуры, возникающих из-за вычислительных погрешностей (алгоритмы компенсации приведены ниже). Однако этих формул достаточно, чтобы показать возможность эффективного распараллеливания по схеме SIMD: очевидно, что основные этапы алгоритма заключаются в проведении над каждым из ионов поочерёдно одних и тех же операций. Наиболее критичным участком алгоритма является расчёт результирующих сил, действующих на каждый из ионов со стороны остальных. Этот расчёт необходим на каждом шаге молекулярной динамики, а его объём квадратичен по количеству частиц N, так как для каждой из N частиц необходимо выполнить суммирование сил, действующих со стороны N-1 остальных:
Поскольку для реалистичного моделирования модельные кристаллиты должны содержать десятки и сотни тысяч ионов, объём расчёта очень велик по сравнению с расчётами на остальных этапах алгоритма. Именно этот расчёт имеет смысл в первую очередь реализовать на графических процессорах. Нам такая реализация позволила на порядки ускорить молекулярно-динамическое моделирование ионных кристаллов (диоксида урана). 6.2. Программирование графического процессора для расчёта действующих на ионы результирующих сил Расчёт сил, действующих на ионы в молекулярной динамике, мы рассмотрим на конкретном примере нашего решения этой задачи. Структура исходных данных и алгоритм получения результата в данном случае несколько более сложны, чем в предыдущем примере сложения матриц. Прежде, чем переходить к анализу текстов программ, опишем подробнее исходные данные и ожидаемый результат.
|

 ,
, - некулоновский потенциал взаимодействия электроновских оболочек.
- некулоновский потенциал взаимодействия электроновских оболочек.
 .
.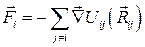 ;
; .
.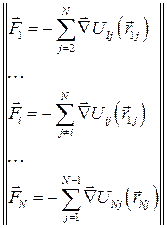 .
.


