Исходные данные и метод восстановления потенциалов
В качестве опорных экспериментальных данных для восстановления параметров парных потенциалов взаимодействия (ПП) мы использовали зависимости теплового расширения периода кристаллической решетки различных типов АО-топлива при атмосферном давлении [37]. МД моделирование проводили в периодических граничных условиях (ПГУ) для исключения поверхностных эффектов; тогда объем модельного кристалла при данной температуре связан с его периодом решетки соотношением: V (T) = c * L (T)3, где с – количество элементарных ячеек в периодически-транслируемой кубической области. Искали параметры ПП, которые минимизируют среднеквадратичное отклонение периода решетки (или объема кристалла с заданным числом частиц) от экспериментального во всем диапазоне температур от комнатной до точки плавления 300~3100К при нулевом внутреннем давлении. Атмосферным давлением ~0.1 МПа пренебрегали в сравнении с давлениями 0.3~3 ГПа (см. рис. 1 и рис. 2), возникающими в кристалле при отклонениях периода решетки на 0.001~0.01 ангстрем (далее просто Å). Для получения среднего периода решетки в «изобарном» МД-моделировании (при заданном числе частиц, давлении и температуре – NPT) требуется релаксация к равновесию и усреднение колебаний объема кристалла под действием баростата с периодом порядка 1-10 пикосекунд (далее просто пс), который определяется константой баростата. При этом из уравнения состояния следует, что отклонения объема при данной температуре однозначно определяются соответствующими отклонениями давления – к примеру, непосредственно из определения изотермической сжимаемости: dlnV = –BTdP. Однако, для получения среднего давления в «изохорном» МД-моделировании (при заданном числе частиц, объеме и температуре – NVT) требуется релаксация к равновесию и усреднение лишь тепловых колебаний частиц около положений равновесия, период которых меньше на 1-2 порядка ~0.1 пс (см. табл. 8.1). Таблица 8.1 Сравнение NVT и NPT типов МД-моделирования.
Рис. 8.1. Колебания давления и «средние» при разных температурах в NVT МД.
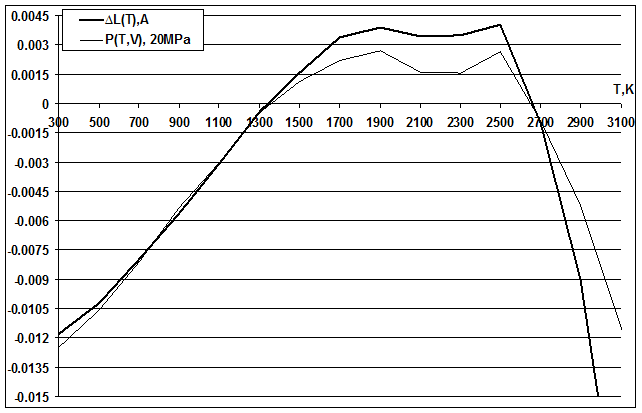
Рис. 8.2. Отклонения давления и периода от их экспериментальных температурных зависимостей, приведенные к одному масштабу. Поэтому для решения оптимизационной задачи за наименьшее время мы использовали NVT -моделирование (при постоянстве количества частиц, объёма и температуры) и минимизировали отклонения от экспериментальных значений уравнения состояния по давлению, вместо объема (периода решетки), а NPT -моделирование (при постоянном нулевом давлении вместо постоянства объёма) температурной зависимости периода решетки применяли лишь для заключительной оценки качества полученных ПП. На рис. 8.1 показаны характерные кривые колебаний давления для NVT -моделирования диоксида урана при температурах 300 К (комнатной) и 3100 К (близкой к плавлению) и их усреднение по времени. Видно, что на временах порядка 10 пс «средние» приходят к своим равновесным значениям. На рис. 8.2 приведены графики отклонения периода и давления от экспериментальных при одинаковом масштабе, видно, что кривая давления (в NVT) воспроизводит все особенности температурной зависимости отклонения периода (в NPT) – знаки функции и первых двух производных. Тем не менее, можно отметить количественные отличия между кривыми, нарастающие с температурой, эти отличия обусловлены нелинейной зависимостью уравнения состояния твердого тела от температуры. Поэтому оценка отклонений периода по давлению на высоких температурах является заниженной (максимальное отличие наблюдается вблизи плавления и достигает ~0.01 Å).
|