МИСТЕРСТВО СТРОИТЕЛЬНОГО КОМПЛЕКСА И ЖИЛИЩНО-КОММУНАЛЬНОГО ХОЗЯЙСТВА
Розглянемо послідовність {xn} = Якщо послідовність {xn} монотонна й обмежена, то вона має кінцеву границю. За формулою бінома Ньютона:
або, що те ж саме
Покажемо, що послідовність {xn} – зростаюча. Дійсно, запишемо вираз xn+1 і зрівняємо його з виразом xn:
Кожен доданок у виразі xn+1 більший відповідного значення xn, і, крім того, в xn+1 додається ще один позитивний доданок. Таким чином, послідовність {xn} зростаюча. Доведемо тепер, що при будь-якому n її члени не перевершують трьох: xn < 3.
геометрична прогресія Отже, послідовність
З нерівності
переходячи до границі, одержуємо
Таким чином, число е укладене між числами 2, 5 й 3. Якщо взяти більшу кількість членів ряду, то можна одержати більш точну оцінку значення числа е. Можна показати, що число е ірраціональне і його значення дорівнює 2, 71828... Аналогічно можна показати, що Припустимо:
Знайдемо Число е є основою натурального логарифма.
Рис. 1.3
Вище наданий графік функції y = lnx.
2. ГРАНИЦЯ ФУНКЦІЇ
Поняття границі функції є узагальненим поняттям границі послідовності, тому що границю послідовності можна розглядати як границю функції xn = f(n) цілочисельного аргументу n. Визначення. Число А називається границею функції
виконується нерівність
Якщо число А границя функції в точці
Геометричний зміст границі функції у точці
Рис. 2.1
ЗАУВАЖЕННЯ. Визначення границі не вимагає існування функції у самій точці
Визначення. Якщо f(x) ® A1 при х ® а тільки при x < a, то
f(x)
А2
А1
0 a x
Рис. 2.2 Наведене вище визначення ставиться до випадку, коли функція f(x) не визначена в самій точці х = а, але визначена в деякій як завгодно малій околиці цієї точки. Границі А1 й А2 називаються також однобічними границями функції f(x) у точці х = а. Також говорять, що А – кінцева границя функції f(x).
Визначення. (у нескінченності) Число А називають границею функції
Геометричний зміст границі функції у нескінченності
Рис. 2.3 Приклад Довести, що Для
Визначення. Функція
Приклад. Функція f(x) = xn є нескінченно малою при х®0 і не є нескінченно малою при х®1, тому що
2.1. Властивості нескінченно малих функцій
1) Сума фіксованого числа нескінченно малих функцій при х 2) Добуток фіксованого числа нескінченно малих функцій при х 3) Добуток нескінченно малої функції на функцію, обмежену поблизу точки х = а є нескінченно малою функцією при х 4) Частка від розподілу нескінченно малої функції на функцію, границя якої не дорівнює нулю, є величина нескінченно мала.
Визначення. Функція Якщо нескінченно велика функція приймає в деякій околиці тільки невід’ємні (від’ємні) значення, то Графічно наведені вище випадки можна проілюструвати в такий спосіб:
a x a x a x
Рис. 2.4
2.2. Порівняння нескінченно малих функцій
Нехай Наприклад, функція f(x) = x10 наближається до нуля швидше, ніж функція f(x) = x. Визначення. Якщо
Визначення. Якщо
Визначення. Якщо
Приклад. Зрівняємо нескінченно малі при х®0 функції f(x) = x10 й f(x) = x.
тобто функція f(x) = x10 – нескінченно мала більш високого порядку, ніж f(x) = x.
Визначення. Нескінченно мала функція a називається нескінченно малою порядку k відносно нескінченно малої функції b, якщо границя
Однак слід зазначити, що не всі нескінченно малі функції можна порівнювати між собою. Наприклад, якщо відношення
Приклад. Якщо
Приклад. Якщо
2.3. Властивості еквівалентних нескінченно малих 1) a ~ a, 2) Якщо a ~ b і b ~ g, то a ~ g, 3) Якщо a ~ b, то b ~ a, 4) Якщо a ~ a1 й b ~ b1 й
Наслідок: а) якщо a ~ a1 й б) якщо b ~ b1 й Властивість 4 особливо важливо на практиці, тому що вона фактично означає, що границя відносини нескінченно малих не міняється при заміні їх на еквівалентні нескінченно малі. Цей факт дає можливість при знаходженні границь заміняти нескінченно малі на еквівалентні їм функції, що може сильно спростити обчислення границь. Корисно мати на увазі еквівалентність наступних нескінченно малих: якщо
Приклад. Знайти границю Так як tg5x ~ 5x й sin7x ~ 7x при х
Приклад. Знайти границю
Приклад. Знайти границю Тому що 1 – cosx =
Приклад. Знайти границю Якщо a і b – нескінченно малі при х®а, причому b – нескінченно мала більш високого порядку, аніж a, то g = a + b – нескінченно мала, еквівалентна a. Це можна довести наступною рівністю Тоді говорять, що a – головна частина нескінченно малої функції g.
Приклад. Функція х2 +х – нескінченно мала при х®0, х – головна частина цієї функції. Щоб показати це, запишемо a = х2, b = х, тоді
2.4. Теореми про границі
Практичне обчислення границь базується на наступних теоремах про границі: якщо існують
1. 2.
3. 4. 5.
А також на теоремах про граничний перехід під знаком неперервної функції: якщо
3. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
На практиці для обчислення границь велике значення мають такі границі: 1. 2. 3. де P(x) = a0xn + a1xn-1 +…+an, Q(x) =b0xm+b1xm-1+…+bm – багаточлени.
Разом:
Крім цього, можна записати наступні корисні на практиці співвідношення:
Якщо функція є елементарною та якщо граничне значення аргументу належить до її області визначення, то обчислення границі зводиться до простої підстановки граничного значення аргументу. Тобто границя елементарної функції
Розглянемо випадки, коли границю функції не можна визначити шляхом підстановки замість аргументу його граничного значення (невизначеності
I. Випадок, коли функція, яка стоїть під знаком границі при
Тобто Якщо
Приклад. Знайти границю
Спочатку переконуємось у тому, що маємо невизначеність
Приклад. Знайти границю
Спочатку переконуємось, що маємо невизначеність
II. Випадок, коли функція, яка стоїть під знаком границі при Тобто У цьому випадку шляхом тотожних алгебраїчних або тригонометричних перетворень необхідно скоротити дріб.
Приклад. Знайти границю
Спочатку переконуємось у тому, що маємо невизначеність типу
Приклад. Знайти границю
Приклад. Знайти границю
Приклад. Знайти границю
Розкладемо чисельник і знаменник на множники.
x2 – 3x + 2 = (x – 1)(x – 2). Таким чином, можна записати x2 – 5x + 6 = (x – 2)(x – 3), тому що
x3 – x2 x2 – 5x + 6. - 5x2 + 11x - 5x2 + 5x 6x - 6 6x - 6 0 Тоді
III. Випадок, коли функція, яка стоїть під знаком границі при
Тобто Цей випадок невизначеності можна привести до розглянутих раніше випадків Приклад. Знайти границю
IV. Випадок, коли при
Тобто Цей випадок, як і попередній, можна привести до розглянутих раніше випадків невизначеностей типів Приклад. Знайти границю маємо невизначеність типу (
V. Випадок, коли при Тобто Приклад. Знайти границю
=
Приклад. Знайти границю.
4. ІНДИВІДУАЛЬНІ ЗАВДАННЯ Знайти границі 1 варіант 1. 3. 5. 7. 9.
2 варіант 1. 3. 5. 7. 9. 3 варіант 1. 3. 5. 7. 9. 4 варіант 1. 3. 5. 7. 9. 5 варіант 1. 3. 5. 7. 9. 6 варіант 1. 3. 5. 7. 9. 7 варіант 1. 3. 5. 7. 9. 8 варіант 1. 3. 5. 7. 9. 9 варіант 1. 3. 5. 7. 9. 10 варіант 1. 3. 5. 7. 9. 11 варіант 1. 3. 5. 7. 9. 12 варіант 1. 3. 5. 7. 9. 13 варіант 1. 3. 5. 7. 9. 14 варіант 1. 3. 5. 7. 9. 15 варіант 1. 3. 5. 7. 9. 16 варіант 1. 3. 5. 7. 9.
17 варіант 1. 3. 5. 7. 9.
18 варіант 1. 3. 5. 7. 9. 19 варіант 1. 3. 5. 7.
|

 .
.
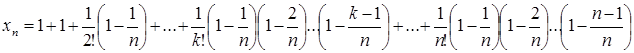

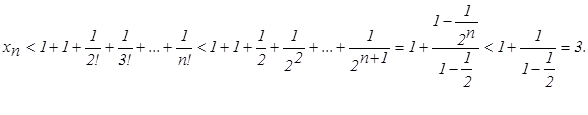
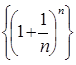 – монотонно зростаюча та обмежена зверху, тобто має кінцеву границю. Цю границю прийнято позначати буквою е.
– монотонно зростаюча та обмежена зверху, тобто має кінцеву границю. Цю границю прийнято позначати буквою е. .
.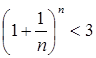 треба, щоб е £ 3. Відкидаючи в рівності для {xn} всі члени, починаючи із четвертого, маємо:
треба, щоб е £ 3. Відкидаючи в рівності для {xn} всі члени, починаючи із четвертого, маємо: ,
,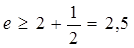 .
.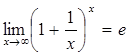 , розширивши вимоги до х до будь-якого дійсного числа:
, розширивши вимоги до х до будь-якого дійсного числа: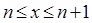 ;
; ;
;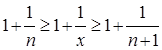 ;
; .
.



 у точці
у точці  (або при
(або при  ), якщо для будь-якого як завгодно малого числа
), якщо для будь-якого як завгодно малого числа  можна знайти таке число
можна знайти таке число 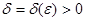 , що для
, що для  , які задовольняють нерівність
, які задовольняють нерівність
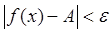 .
. або
або 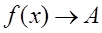 при
при 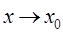 . (2.2)
. (2.2)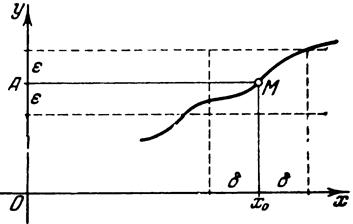
 в деякій околиці точки
в деякій околиці точки 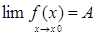 , ми припускаємо, що
, ми припускаємо, що  – називається границею функції f(x) у точці х = а ліворуч, а якщо f(x) ® A2 при х ® а тільки при x > a, то
– називається границею функції f(x) у точці х = а ліворуч, а якщо f(x) ® A2 при х ® а тільки при x > a, то 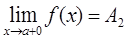 називається границею функції f(x) у точці х = а праворуч.
називається границею функції f(x) у точці х = а праворуч. в
в при
при 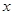 , що прагне до
, що прагне до 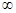 , якщо для
, якщо для 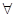 , навіть як завгодно малого невід’ємного числа
, навіть як завгодно малого невід’ємного числа 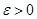 , знайдеться таке невід’ємне число S=S(
, знайдеться таке невід’ємне число S=S(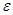 ), що для всіх таких
), що для всіх таких  виконується нерівність
виконується нерівність 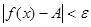 . Позначають
. Позначають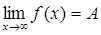 . (2.3)
. (2.3)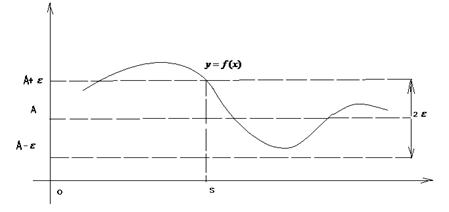
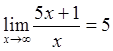 .
. :
: 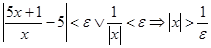 . Отже для
. Отже для  число
число  таке, що для всіх
таке, що для всіх  буде виконуватись
буде виконуватись  , де
, де 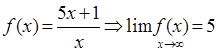 .
.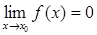 .
.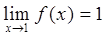 .
. а теж нескінченно мала функція при х
а теж нескінченно мала функція при х 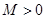 знайдеться таке число
знайдеться таке число 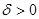 , що для всіх значень
, що для всіх значень 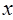 , які входять в область визначення функції (
, які входять в область визначення функції (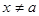 ) та задовольняють нерівності
) та задовольняють нерівності 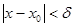 , має місце нерівність
, має місце нерівність  . Записують таким чином:
. Записують таким чином:  .
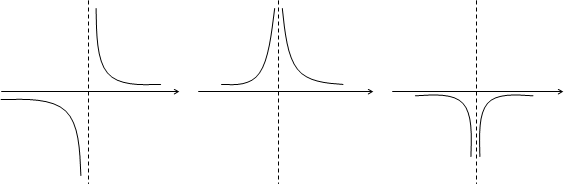
. , (
, ( ).
).
 (х),
(х),  (х) і
(х) і  (x) – нескінченно малі функції при х
(x) – нескінченно малі функції при х 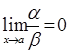 , то функція a називається нескінченно малою більш високого порядку, ніж функція b.
, то функція a називається нескінченно малою більш високого порядку, ніж функція b.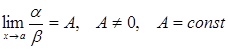 , то a і b називаються нескінченно малими одного порядку.
, то a і b називаються нескінченно малими одного порядку. то функції a і b називаються еквівалентними нескінченно малими. Записують
то функції a і b називаються еквівалентними нескінченно малими. Записують 
 кінцева й відмінна від нуля.
кінцева й відмінна від нуля. не має границі, то функції непорівнянні.
не має границі, то функції непорівнянні. , то при х®0
, то при х®0  , тобто функція a – нескінченно мала порядку 2 щодо функції b.
, тобто функція a – нескінченно мала порядку 2 щодо функції b.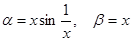 , то при х®0
, то при х®0  не існує, тобто функції a і b непорівнянні.
не існує, тобто функції a і b непорівнянні. .
. .
.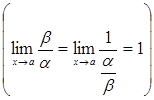 .
. , то й
, то й  або
або  .
.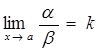 , то й
, то й 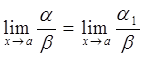 ;
; , то
, то 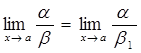 .
.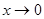 , то
, то ~x, tgx~x, arcsinx~x, arctgx~x, ln(1+x)~x.
~x, tgx~x, arcsinx~x, arctgx~x, ln(1+x)~x. .
.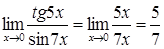 .
. .
. .
. при х®0, то
при х®0, то  .
.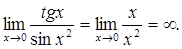
 .
. .
. та
та 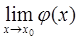 , то:
, то: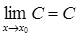 , де С = const.
, де С = const. =
= 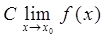 , де С = const.
, де С = const. =
= 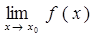

 .
.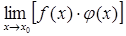 =
= 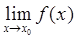
 .
. =
=  , де (
, де (
 ).
).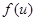 неперервна у точці
неперервна у точці 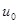 та
та 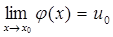 , то
, то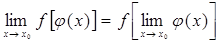 .
. (перша визначна границя).
(перша визначна границя).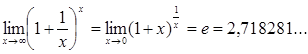 (друга визначна границя).
(друга визначна границя).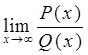 ,
,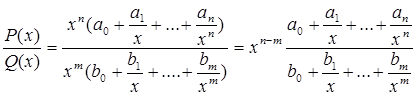 ;
; .
.
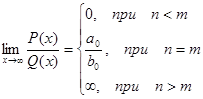

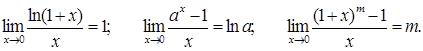
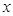 наближається до значення
наближається до значення 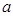 , яке входить до області визначення функції, дорівнює приватному значенню функції при
, яке входить до області визначення функції, дорівнює приватному значенню функції при 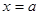 :
: .
. , (
, (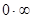 ),
), 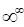 ,
,  ,
, 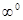 ). У цих випадках необхідно проводити додаткові дослідження, основані на тотожних перетвореннях функції.
). У цих випадках необхідно проводити додаткові дослідження, основані на тотожних перетвореннях функції.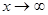 , – це відношення двох нескінченно великих величин (невизначеність типу
, – це відношення двох нескінченно великих величин (невизначеність типу 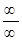 ).
). ,
,  =
= 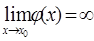 .
.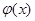 – раціональні функції, то числівник та знаменник дробу необхідно розділити на найвищий степінь
– раціональні функції, то числівник та знаменник дробу необхідно розділити на найвищий степінь  .
.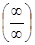 , зробимо деякі перетворення. Розділимо числівник і знаменник на
, зробимо деякі перетворення. Розділимо числівник і знаменник на 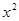 (найбільший степінь числівника та знаменника):
(найбільший степінь числівника та знаменника): =
=  =
=  .
.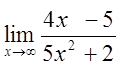 .
.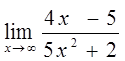 =
=  =
=  .
. ).
). ,
, 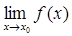 =
=  .
.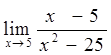 .
. , зробимо деякі перетворення, а саме:
, зробимо деякі перетворення, а саме: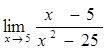 =
=  =
= 
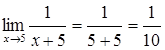 .
.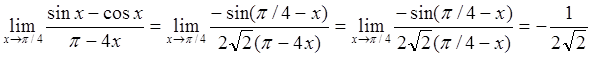 .
.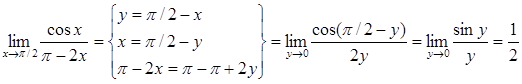 .
.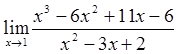 .
.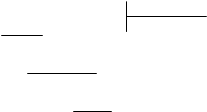 x3 – 6x2 + 11x – 6 x - 1
x3 – 6x2 + 11x – 6 x - 1 .
. ).
).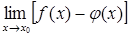 ,
, 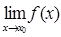 =
= 
 – невизначеність типу (
– невизначеність типу (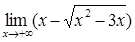 =
= 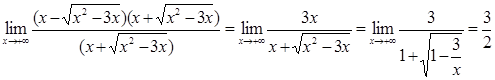 .
.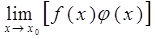 ,
,  =0,
=0, 
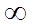 .
. ,
, , тоді отримаємо:
, тоді отримаємо: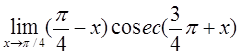 =
= 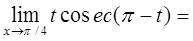
 .
. ).
). ,
, 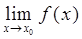 =1,
=1,  =
=  . У цьому випадку знаходження границі зводиться до другої визначної границі.
. У цьому випадку знаходження границі зводиться до другої визначної границі.
 =
= 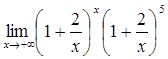 =
= 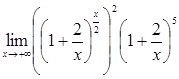 =
=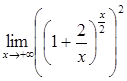
 =
=  .
.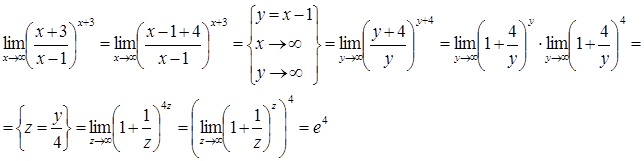
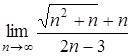 2.
2. 
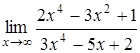 4.
4. 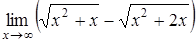
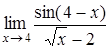 6.
6. 
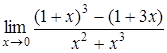 8.
8. 
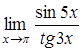 10.
10. 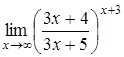
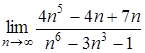 2.
2. 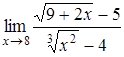
 4.
4. 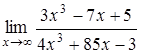
 6.
6. 
 8.
8. 
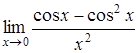 10.
10. 
 2.
2. 
 4.
4. 
 6.
6. 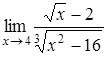
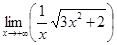 8.
8. 
 10.
10. 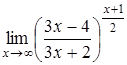
 2.
2. 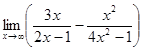
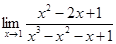 4.
4. 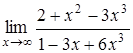
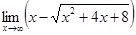 6.
6. 
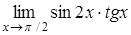 8.
8. 
 10.
10. 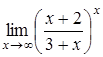
 2.
2. 
 4.
4. 
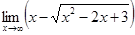 6.
6. 
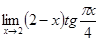 8.
8. 
 10.
10. 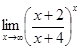
 2.
2. 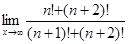
 4.
4. 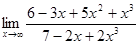
 6.
6. 
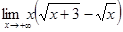 8.
8. 
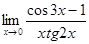 10.
10. 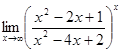
 2.
2. 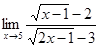
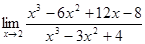 4.
4. 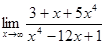
 6.
6. 
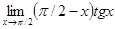 8.
8. 
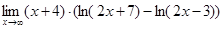 10.
10. 
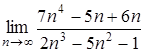 2.
2. 
 4.
4. 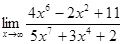
 6.
6. 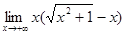
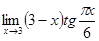 8.
8. 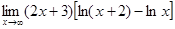
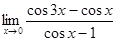 10.
10. 
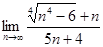 2.
2. 
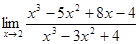 4.
4. 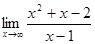
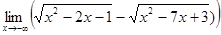 6.
6. 
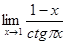 8.
8. 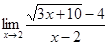
 10.
10. 
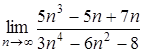 2.
2. 
 4.
4. 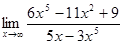
 6.
6. 
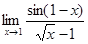 8.
8. 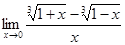
 10.
10. 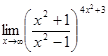
 2.
2. 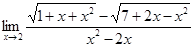
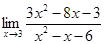 4.
4. 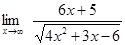
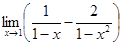 6.
6. 
 8.
8. 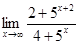
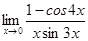 10.
10. 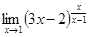
 2.
2. 
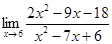 4.
4. 
 6.
6. 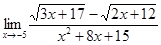
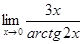 8.
8. 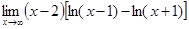
 10.
10. 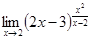
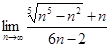 2.
2. 
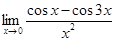 4.
4. 
 6.
6. 
 8.
8. 
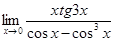 10.
10. 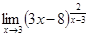
 2.
2. 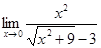
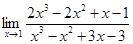 4.
4. 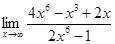
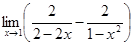 6.
6. 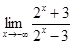
 8.
8. 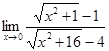
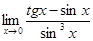 10.
10. 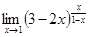
 2.
2. 
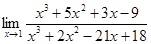 4.
4. 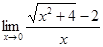
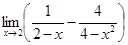 6.
6. 
 8.
8. 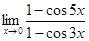
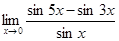 10.
10. 
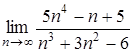 2.
2.  4.
4. 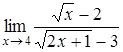
 2.
2. 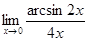
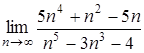 2.
2. 
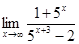
 2.
2. 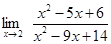 4.
4. 


