Линейный нониус и штангенциркуль
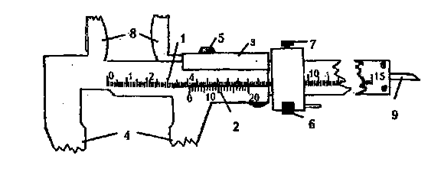
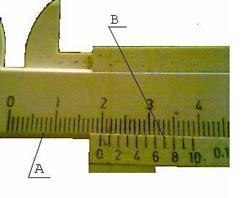
К числу простейших физических измерений относятся определения линейных и угловых размеров тел, их объема, а также массы. Для увеличения точности многих измерительных приборов служит устройство, называемое нониусом. Линейный нониус штангенциркуля (Рис.4)представляет собой неболь
Рис.4
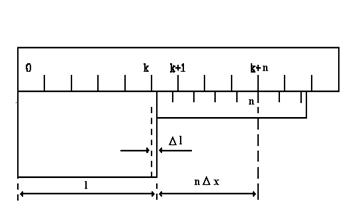
шую линейку А, скользящую вдоль основного масштаба В, на этой линейке А нанесена шкала, состоящая из m делений (Рис.5). Каждое из делений нониуса имеет длину X. Длина наименьшего деления основного масштаба Y. Длина нониуса подбирается равной длине целого числа наименьших делений основной шкалы. При этом каждое деление нониуса будет меньше соответствующего деления шкалы z на определенную часть наименьшего деления масштаба y: z = cy, где c –произвольное число. Величина D x=z–x=cy–x (I.1) называется точностью нониуса. Обычно в теории рассматривается случай, когда Z = Y, т.е. каждое деление нониуса на величину D x меньше наименьшего деления шкалы Y. Однако на практике для удобства измерений " растягивают" нониус так, что каждое его деление становится на величину x меньше определенного, но не наименьшего деления основной шкалы Z. Мы рассматриваем этот, более общий случай. По конструкции нониуса длина всех его m делений меньше длины такого же числа m делений z основной шкалы на длину наименьшего деления основной шкалы y: mx=cmy–y=(cm–1)y. Отсюда mcy–mx=y, и точность нониуса D x=cy – x=y / m (I.2)
Рис.5
|