Функция случайной величины и ошибка в ее определении
В большинстве случаев искомая величина не может быть измерена непосредственно, а определяется через другие, которые можно измерить. Например, для определения объема шара мы измеряем его диаметр d и потом вычисляем объем Во всех подобных случаях мы имеем дело с функцией случайной величины, т. к. истинного значения аргумента (в данном случае диаметра) мы не знаем. Но если значение аргумента находится с определенной степенью точности, то и зависящая от него функция также определяется с ошибкой. На рис.2 представлен график зависимости V от d, из которого видно, что интервалу d значений аргумента соответствует интервал ∆ V значений функции. Среднему же значению диаметра d ср будет соответствовать среднее значение объема V ср.
Обозначим в общем случае функцию случайной величины буквой Z, а аргумент – буквой А, тогда
|
. Таким образом, объем в данном случае есть функция диаметра, а сам диаметр измерен с некоторой ошибкой и представляет собой целый ряд значений внутри интервала, ширина которого этой ошибкой обусловлена.
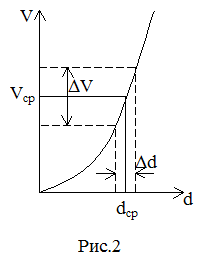
. Вид этой функции может быть различным. Наиболее распространенные варианты подобных функций и указания, как найти ошибку в ее определении ∆ Z, если задана ошибка в определении аргумента ∆ А, даны в Приложении 4. В общем случае Z = Z (A): абсолютная погрешность измерения будет равна 
, где 
определяет степень зависимости Z от А в интересующей нас точке.
