Функция нескольких переменных (ошибки косвенных измерений)
Часто встречаются случаи, когда искомая функция зависит от нескольких величин, каждая из которых определяется с ошибкой. Например, объем цилиндра зависит как от радиуса r (или диаметра d), так и от высоты h:
Общую функциональную зависимость в этом случае можно представить в виде В этом случае для каждой серии измерений
При этом мы можем указать знак отклонения в большую или меньшую сторону) для D А и D В. Для данной серии может получиться, что знаки ошибок противоположны и скомпенсируют друг друга, однако это не говорит о большой точности измерения. Чтобы избежать зависимости от знака ошибки при усреднении по всем сериям, пользуются следующим способом. Возведем в квадрат выражение для D Z:
Затем, усреднив по сериям и учитывая, что в связи со случайным, но равновероятным появлением знаков (+) и (–) у D А и D В
Пример. Найдем ошибку в определении объема цилиндра. Сначала определим частные производные:
Абсолютная погрешность в определении объема будет:
Если Z - функция произвольного числа аргументов, т. е. Z = Z (A, B, D, E....), то среднеквадратичная ошибка среднего
Пользуясь обозначениями дифференциального исчисления, погрешность величины у, представляющей собой функцию от переменных х 1, х 2, …, х n: у = f (х 1, х2, …, х n), можно записать в виде
где D х 1, D х 2, …, D х n - абсолютные погрешности х 1, х 2, …, х n соответственно, ¶f/¶x1, ¶f/¶x2, …, ¶f/¶xn – частные производные у по переменным х 1, х 2, …, х n соответственно. Частная производная функции многих переменных f (х 1, х 2, …, х n) по одной переменной, допустим х 1, является обычной производной функции f по х 1, причем, другие переменные х 2, …, х n считаются постоянными величинами. Все производные вычисляются при значениях х 1 = х 1ср, х 2 = х 2ср, …, х n = х nср. Относительную погрешность величины у можно вычислить согласно формуле:
Поскольку
Рассмотрим в качестве примера функцию трех переменных u = x a y b/ z g, где a, b, g – любые рациональные числа, тогда относительную погрешность измерения величины u можно рассчитать по формуле: eu = (a2ex 2 + b2ey 2 + g2ez 2)1/2, где ex, ey, ez - относительные ошибки измерений величин x, y, z.
При невысокой точности измерительных приборов случайными ошибками обычно можно пренебречь по сравнению с погрешностью измерительного прибора. Для получения результата достаточно одного отсчета. Пусть Z = f(A, B, D, …), где A, B, D, … –непосредственноизмеряемыевеличины, а DA, DB, DD, … –ихабсолютныесистематическиеошибки, тогдаможнопредложить следующий алгоритм нахождения абсолютной ошибки косвенных измерений: 1. Продифференцируем формулу исследуемой величины:
2. Знаки дифференциалов “d” заменяем знаками погрешностей “ D ”, в случае получения в реальной формуле знаков “ – ” у каких-либо частных производных заменяем их на знаки “+”:
В некоторых случаях сначала удобнее находить относительную ошибку и уже затем абсолютную. Пусть функциональная зависимость имеет вид: 1. Прологарифмируем исходную формулу:
2. Продифференцируем полученную в результате логарифмирования формулу:
3. Знаки дифференциалов “d” заменяем знаками погрешностей “ D ”, в случае получения в реальной формуле знаков “ – ” у каких-либо частных производных заменяем их на знаки “+”:
|

 .
. Если D А и D В являются отклонениями измеренных значений от истинных параметров, то степень зависимости D Z от них будет также обусловлена частными производными
Если D А и D В являются отклонениями измеренных значений от истинных параметров, то степень зависимости D Z от них будет также обусловлена частными производными 
 или
или  .
. .
. , получим
, получим .
. .
. .
. , которую мы здесь обозначим как D Z, будет равна:
, которую мы здесь обозначим как D Z, будет равна: .
.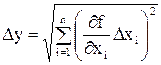 ,
, .
. , то для относительной погрешности получаем
, то для относительной погрешности получаем .
. .
.
 .
. .
. .
. .
.


