Символический метод расчета
Анализ электромагнитных процессов в электрических цепях переменного тока в общем случае возможен только с использованием представления токов, напряжений и параметров цепи комплексными числами. Это позволяет исключить тригонометрические функции из уравнений, описывающих электрическую цепь и сделать их линейными. Так как при этом все величины заменяются их изображениями или символами, то этот метод носит название символического. Последовательность операций в символическом методе в общем случае следующая:
Комплексная форма представления синусоидальных величин (формулы Эйлера).
Мнимая часть комплексного числа вращающегося вектора Применительно к переменному току следует писать в комплексном виде:
Индуктивность
uL=-LdiL/dt=ω L ILm cos(ω t+ψ i)=ULm sin(ω t+ψ i+π /2)=ULmsin(ω t+ψ u),
В индукт. элементе вектор напряжения опережает вектор тока на π /2. ХL=ω L(> 0) [om]- индуктивное сопротивление При постоянном токе ω =0 индуктивность не оказывает никакого сопротивления, а при ω > 0 сопротивление индуктивности возрастает.
Аналогично действуем для емкостного элемента. UC=UCm sin(ω t+ψ u), IC =dq/dt, IC=C dUC/dt=ω C UCm cos(ω t+ψ u)=ICm sin(ω t+ψ u+π /2))=ICm sin(ω t+ψ I),
В ёмкости вектор тока опережает вектор напряжения на π /2. ICm= ω C UCm, UC=IC/ ω C=IC/BC, BC= ω C -емкостная проводимость [ом-1], С ХС=-1/ ω C (< 0)[- емкостное сопротивление. Для постоянного тока ω =0 ёмкость разрывает эл цепь, а при ω =∞ -ёмкость не имеет сопротивления. Полное сопротивление индуктивной и емкостной цепи
Энергетические процессы в резистивном, индуктивном и ёмкостном элементах. Резистивный элемент. Ur=Urm sinω t, Ir=Ur/R=Irm sinω t. Мощность мгновенная pr=Ur Ir=Urm Irm sin 2 ω t = Urm Irm/2 (1-cos2ω t) Средняя за период мощность Pr= Индуктивный элемент: напряжение ul=L dil/dt=Ulm cosω t опережает по фазе на угол π /2 ток il=Ilm sinω t. Мгновенная мощность pl=ul il=Uml Iml sin ω t cos ω t= Uml Iml /2 sin 2 ω t. Средняя за период Т значение мощности Рl=∫ pl dt/T=0.Синусоидальный ток в индуктивном элементе не совершает работы. За первые четверть периода происходит накопление энергии, а за следующую четверть – отдаёт в сеть энергию. Поэтому энергетический режим работы индуктивного элемента принято определять не активной, а реактивной индуктивной мощностью, равной максимальному положительному значению мгновенной мощности: QL=UL IL=XL IL2. Емкостной элемент: напряжение uc=(1/C) ∫ ic dt=-Ucm cos ω t отстаёт по фазе от тока на угол π /2 от тока. Мгновенная мощность pc=uc ic=-Uc Ic sin 2 ω t. Емкостной элемент, как и индуктивный, то заряжается, от отдаёт энергию в электрическую сеть; как и индуктивный элемент ёмкость не совершает работы. Реактивная мощность ёмкости равна максимальному отрицательному значению мгновенной мощности: QC=-UC IC=-XC IC2. Полная мощность электрической цепи: S=U I=Z I2 [B·A], S2=P2+Q2, Q=X I2[B AP], X=XL-XC-реактивное сопротивл. Колебания энергии в элементах цепи переменного тока.
В катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС, в отличие от активного сопротивления R резистора, – реактивными
Из предыдущих рисунков видно, что при накоплении энергии в первую четверть периода индуктивностью, ёмкость в этот момент отдаёт в сеть накопленную в ней энергию. Затем всё меняется на обратное z2=r2+(xl-xc)2. Средняя мощность потребителя энергии.
S=U I [VA]-полная мощность, Q=U I sinφ [Вар]-реактивная мощность ей обмениваются составляющие электрической схемы.S 2=P2a+Q2. Cosφ -коэффициент мощности. В состав Ё - мобиля входят: генератор постоянного или переменного тока, тяговый электродвигатель, система управления ТС (транспортное средство) и емкостный накопитель энергии. Накопитель посредством блока управления подключают к тяговому двигателю при разгоне ТС, чтобы обеспечить ускорение (или торможение для заряда конденсаторов от кинетической энергии ТС).
Таким образом городской автомобиль с комбинированной энергоустановкой разгоняется за счет конденсаторов (суперконденсаторов на Ё-мобиле). Они способны отдать накопленную энергию куда большей мощности, чем аккумуляторы, ибо внутреннее сопротивление конденсаторов на порядок меньше такого же сопротивления аккумуляторов. Суперконденсаторы (ионисторы), предлагаемые к производству в рамках проекта относятся к классу конденсаторов, использующих энергию заряда, сосредоточенного в двойном электрическом слое. Напряжение одного суперконденсатора составляет 1, 8...3 В, номинальная емкость до 5000 Ф (емкость земного шара 0.7 Ф), вес до 1 кг., габарит 95 мм. на 120 мм. В процессе эксплуатации и хранения ионисторы не требуют обслуживания, работоспособны в широком интервале температур (-40...+70С), имеют длительный срок эксплуатации. Большинство ионисторов имеют низкий саморазряд и малую величину внутреннего сопротивления(менее 1 мОм). Энергия, запасаемая ионисторами может достигать 50-60 дж/г, а мощность десятки кВт/кг. Суперконденсаторы могут широко применяться в качестве кратковременных перезаряжаемых источников тока с очень большим количеством циклов в режиме " заряд-разряд". Количество циклов до 1 млн. Рабочие токи ионисторов до 1000 А. Кроме того, конденсаторы заряжаются за сколь угодно малое время, аккумуляторы же — в лучшем случае за несколько часов. Значит, городской автомобиль с такой энергоустановкой всегда готов к эксплуатации, что не присуще машинам, использующим аккумуляторы. При этом удельная мощность конденсаторов на много порядков выше аналогичных показателей других накопителей энергии, о чем говорит таблица. Показатели некоторых накопителей энергии
Одна из блок-схем городского автомобиля будущего. По схеме ДВС значительно меньшей мощности, чем ДВС обычного автомобиля, вращает генератор электроэнергии. Она поступает в емкостный накопитель, а уж из него — в тяговый электродвигатель, которым вращаются колеса транспортного средства. Количество электроэнергии, необходимое для того или иного маневра ТС, регулируется электронными устройствами. При торможении тяговый электродвигатель работает в режиме генератора, отдавая анергию в конденсатор-накопитель для использования при последующем разгоне или для запуска двигателя после остановки. Теперь ДВС, который в новом типе автомобиля не связан с механической трансмиссией, можно размещать спереди, сзади и даже на прицепной тележке. При торможении автомобиля энергия, накопленная движущейся массой, легко преобразуется электродвигателем обратно в электрическую и вновь используется для разгона (например, после светофора).
Резонанс в цепи переменного тока Резонанс напряжений в последовательной цепи. I=U/Z=U/√ [R2+(ω L-1/ω C)2]-действующее значение тока. При ω L=1/ω C, L=1/ω рез C, ω рез=1.√ (LC) наступает резонанс напряжения I=U/R-максимален, а ток и напряжение совпадают по фазе. Резонанс токов в параллельной цепи.
Действующее значение тока I=U √ [G2+(1/(ω L)-ω C)2] При 1/(ω L)=ω C, ω рез=1.√ (LC) общий ток минимален I=U G. Законы Ома и Кирхгофа в комплексной форме. Резистор
Индуктивность
jXL-комплексное сопротивление индуктивности. 1/jXL=-jBL-комплексная проводимость ЕМКОСТЬ
1/jω C=-jXc-комплексное сопротивление емкости, jω C-комплексная проводимость.
Законы Кирхгофа в комплексном виде. Первый закон (для узлов)
Второй закон Кирхгофа.
Многофазные системы. Объединение в одну цепь нескольких однофазных цепей одной частоты с независимыми источниками в технике широко используется (многофазные системы). Распространена трехфазная система.(Доливо - Добровольский -1862-1919г) Они широко используются для передачи и распределения энергии. Источник -трехфазный генератор с тремя обмотками переменного тока. Сдвиг по фазе токов-1200. Соединение фаз звездой
Если сопротивления трех приемников одинаковы, то ток в нейтральном проводе равен нулю, а Ua=Ub=Uc фазные напряжения Uф. Iл=Iф. Uab, Ubc, Uca-линейные напряжения Uл=√ 3 Uф. Если Uл=380 В, то Uф=220 В, если Uл=220 В, то Uф=127 В. Трехфазный двигатель подключают к 3 фазам. Осветительные источники подключаются к фазе и нейтральному проводу. Мощность системы P=3 UФ IФ cosφ =√ 3 UЛ IЛ cosφ
Соединение фаз треугольником
Линейные токи равны Ia=Iab-Ica, Ib=Ibc-Iab, Ic=Ica-Ibc.
Линейные токи IЛ отличаются от фазных токов IФ: IЛ=√ 3 IФ=2 cоs30oIФ., UЛ=UФ. Преимущество соединения треугольником(по сравнению со звездой) взаимная независимость фазных токов. Мощность при переключении с треугольника на звезду PТРЕУГ=3РЗВЕЗДЫ Измерение активной мощности трехфазной системы. У симметричного трехфазного приемника мощности фаз одинаковы и достаточно измерить РФ. Тогда мощность приемника Р=3РФ.
Измерение мощности фаз приёмника. Электрические измерения Объектами электрических измерений являются все электрические и магнитные величины: ток, напряжение, магнитный поток и т.д. Электр. приборами измеряют и неэлектрические величины: температура, давление и т.д., которые для этой цели преобразуются в пропорциональные им электрические величины. Остановимся подробнее на цифровых приборах. Микропроцессоры позволяют существенно повысить точность и производительность измереницй, позволяя дополнительно производить запоминание и обработку результатов измерений. Для исследования сложных объектов применяют автоматические измерительные системы. Измерение любой физической величины заключается в её сравнении с эталоном. Различают прямые измерения (ток в цепи) и косвенные (сопротивление по данным измерений тока и напряжения). Погрешности измерения и классы точности. Абсолютная погрешность: Δ А=Аиз-А. Относительная погрешность: γ o=(Δ А/А) 100%. Приведенная погрешность: γ пр=(Δ А/Аном) 100%. Класс точности прибора определяет допустимую погрешность в пределах классов точности приборов: 0.05, 0.1, 0.2, 0.5, 1, 1.5, 2.5, 4. Потребление энергии приборами. Включение прибора в электрическую сеть изменяет режим работы сети. Прибор не должен существенно влиять на параметры работа цепи.
На рис.12.2 А- измеряет ток, а V-напряжение на R. V/I=R’=R+Ra. R=R’ (1-Ra/R’). Чем меньше Ra, тем точнее показания. На рис. 12.3 I’=I+Iv. I’=I+Iv, G’=I’/V=G+Gv =1/R+1/Rv. Чем больше Rv, тем точнее показания. Механические узлы приборов. Подвижная часть прибора располагается на растяжках (упругие ленты из бериллиевой или оловянно- цинковой ленты), которые могут служить для подвода тока к подвижной части прибора (Рис. 12.4). Кварцевые растяжки применяют на зеркальных гальванометрах (рис.12.6). Противодействующий момент создаётся спиральной пружиной (рис.12.5).
Грузила 6 на рис. 12.5 уравновешивают подвижную часть прибора. Для быстрого измерения нужна система успокоителей. Магнитоиндукционные успокоители (рис.12.7А) основано на взаимодействии вихревых токов, индуцированных в магнитном поле постоянных магнитов 2 в алюминиевой подвижной пластине 1.
подвижного алюминиевого крыла. Системы показывающих приборов.
Магнитоэлектрическая система. Вращающий момент создаётся взаимодействием измеряемого постоянного тока в катушке механизма с полем постоянного магнита. На рис. 12.8 показана система с подвижной катушкой в воздушном зазоре постоянного магнита. Магнитную цепь механизма составляет постоянный магнит 1, магнитопровод 2, полюсные наконечники 3 и цилиндрический сердечник 4. Магнитное поле тока I в активной части проводников длиной L взаимодействует с магнитным полем магнита индукцией В силой F=B I L. Возникает вращающий момент Mвр =2F ω d/2=k I Диаметр каркаса d, ω -число витков катушки. Электромагнитная система. Вращающий момент обусловлен действием магнитного поля измеряемого тока в неподвижной катушке 2 на подвижный ферромагнитный якорь 1 (рис. 12.11).
Вращающий момент равен Мвр =I2 dL(α)/(2 d(α)2, где L(α)- и I индуктивность и ток в катушке. Если ток синусоидальный, то I=C(α) √ α, где C(α)-цена деления. Аналогичная зависимость и для постоянного тока I. Недостаток прибора -неравномерная цена деления, но он прост в изготовлении, дешев и допускает большие перегрузки. Электродинамическая система Вращающий момент создаётся взаимодействием двух катушек с токами.
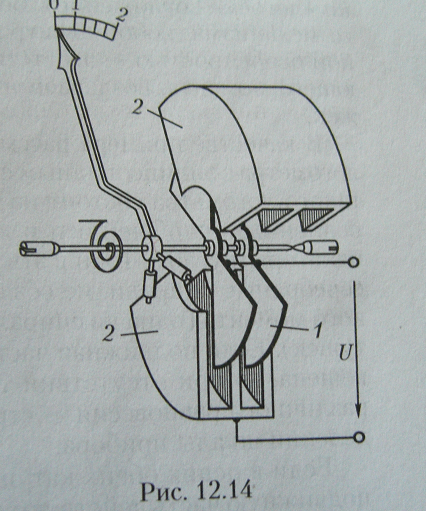
Катушка 1 подвижна, катушка 2- неподвижна. Пружина 3 служит для создания противодействующего момента и подвода тока в подвижную катушку. Магнитный момент равен: Мвр =I1 I2 dL(α)/d(α) Ток пропускается последовательно через катушки 1 и 2. Система может быть использована для измерения напряжения V, тока I и мощности Р=VI. Цена деления неравномерна, но приборы могут быть использованы для измерений при постоянных и переменных токах. Другие системы.. Под действием измеряемого напряжения заряжаются подвижные 1 и неподвижные2 пластины (см. рис.12.14). Возникающие при этом электростатические силы притяжения создают вращающий момент. Противодействуют этому пружины. Прибор пригоден для измерения напряжения в цепях постоянного и переменного тока.
Нелинейные цепи: электрические и магнитные цепи постоянного тока. Обычно электрические цепи содержат нелинейные элементы: резистивные, индуктивные и емкостные, описываемые вольт- амперными I(V), вебер-амперными ψ (i), и кулон- вольтными q(UC) характеристиками.
Нелинейные свойства могут искажать форму токов, а могут и лежать в основе принципа действия, например, выпрямителей, стабилизаторов, усилителей. Включение нелинейного резистора в произвольную линейную цепь. Цепь постоянного тока
Нагрузочная характеристика активного двухполюсника: I=(Eэк-U)/Rэк Точка пересечения А нагрузочной характеристики активного двухполюсника и ВАХ нелинейного элемента определяет рабочий режим цепи, а графоаналитический метод расчета нелинейной цепи- метод нагрузочной характеристики. Последовательное соединение нелинейных элементов в цепи переменного тока Точка А решение задачи
Параллельное соединение нелинейных элементов
Точка А решение задачи
Смешанное соединение нелинейных элементов.
Точка А – решение задачи. Метод двух узлов На предыдущих трех рисунках получения эквивалентной ВАХ последовательного, параллельного и смешанного соединения нелинейных элементов приведены решения задачи определения тока и напряжения в двух узлах 1 и 2.
Графическим решением задачи является точка А пересечения ВАХ эквивалентной нагрузки с внешней характеристикой эквивалентного источника ВАХ=(Eэк-U)/Rэк. Этот метод решения задачи называется методом двух узлов. Понятно, что это решение может быть получено и аналитически. Линеаризация нелинейного сопротивления. Расчет нелинейных цепей удобно вести в рамках линейных приближений характеристик нелинейных сопротивлений (при малых отклонениях от рабочей Р), То есть заменой нелинейного резистора линейным.
где
Линеаризованные схемы замещения. Если исходный режим определен и требуется рассчитать, лишь приращения токов и (или) напряжений, обусловленные изменением напряжения или тока источника, целесообразно использовать эквивалентные схемы для приращений, получаемые на основании законов Кирхгофа для малых приращений: -первый закон Кирхгофа: -второй закон Кирхгофа: При составлении схемы для приращений: 1) все ЭДС и токи источников заменяются их приращениями; 2) нелинейные резисторы заменяются линейными с сопротивлениями, равными дифференциальным в рабочих точках. Необходимо помнить, что полная величина какого-либо тока или напряжения в цепи равна алгебраической сумме исходного значения переменной и ее приращения, рассчитанного методом линеаризации. Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости Магнитные цепи при постоянном магнитном потоке Эрстед в 1820г. продемонстрировал, что вблизи проводника с током возникает магнитное поле. Магнитная цепь-совокупность различных ферримагнитных и неферромагнитных устройств для создания магнитных полей нужных конфигураций и интенсивности.
Различают неразветвленные и разветвленные магнитные цепи. В общем случае магнитная цепь нелинейная. Закон полного тока для магнитной цепи.
Интеграл от напряженности магнитного поля по любому замкнутому контуру равен алгебраической сумме токов, сцепленных с этим контуром.
Н-[А/m]-напряженность магнитного поля. Для магнитного поля, возбужденного катушкой с током I с w витками:
По аналогии с электрическими цепями существуют неразветвленные и разветвленные магнитные цепи. Неразветвленная магнитная цепь Магнитной цепью в электротехнических устройствах называют путь, по которому распространяются и замыкаются магнитные линии. Цепи образуют магнитные системы. Задачей расчета неразветвленной магнитной цепи в большинстве случаев является определение МДС F= Iω, необходимой для того, чтобы получить заданные значения магнитного потока Ф или магнитной индукции В в некотором участке магнитопровода (чаще всего в воздушном зазоре). Если на магнитопроводе расположено к катушек, то МДС определится, как сумма МДС отдельных катушек:
В воздушном зазоре магнита магнитная индукция В2 [T] связана с напряженностью Н2 простым отношением В2= μ Н2 (μ - магнитная проницаемость вещества в зазоре). В ферромагнетике В1=μ 1 Н1. По закону полного тока
где Um1, Um2-магнитные напряжения на различных участках магнитной цепи. В неразветвленной магнитной цепи магнитный поток одинаков в любом сечении магнитопровода (ток в неразветвленной эл. цепи также одинаков): Ф=В1 S1=B2S2. (1) Прямая задача. Пусть задан магнитный поток Ф. Определим МДС F. Из (1) находим В1 и В2. Н1-находим по рис. В1(Н), а Н2=В2/μ o. Тогда МДС определится из выражения: F=B1 L1/μ a+B2 L2/μ o=Iω. Последнее выражение можно записать иначе. Ф{L1/S1μ a+L2/S2μ o}=Ф(Rm1+Rm2)=ФΣ Rmk=Iω =F=Um1+Um2, I=(Eэк-U)/Rэк Для магнитного зазора Ф=(F-Um1)/Rm2, для ферромагнетика Ф=В1(Н1) S1 =Ф(Um1), так как (Н1=Um1/L1) где Rmk=Lk/Skμ k-магнитное (нелинейное) сопротивление к-го участка магнитной цепи. Тогда для последовательной цепи имеем: Ф=Iω /Rm аналог (I=U/R) Последнее выражение по форме напоминает закон Ома для электрической цепи: на месте тока I стоит магнитный поток Ф, на месте напряжения U— намагничивающая сила Iω =HL Существует формальная аналогия между магнитными цепями с постоянными МДС и электрическими цепями постоянного тока. Можно нарисовать схему замещения по аналогии с электр. цепью.
Σ Um=Σ F Что аналогично закону Кирхгофа для замкнутого электрического контура Σ U=Σ Е. Аналогично решаются задачи расчета параллельных (разветвленных) магнитных цепей, где в схемах замещения складываются величины, обратные магнитным сопротивлениям, то есть проводимости. 'По аналогии с ВАХ электрических цепей можно построить Вебер-амперную характеристику Ф(Um). Для нелинейной зависимости магнитной проницаемости ферромагнетика μ а(Н) магнитная индукция В(Н) нелинейна, как нелинейно и магнитное сопротивление Rm1. Магнитное сопротивление зазора линейно, так как магнитная проницаемость зазора не зависит от напряженности Н.
Аналогом ВАХ является нелинейная зависимость ферромагнетика Ф(Um1), аналогом тока I является магнитный поток Ф, аналогом напряжения U есть магнитное напряжение Um, аналогом сопротивления R- магнитное сопротивление Rm С помощью Вебер-амперной характеристики можно получить решение обратной задачи: по заданной величине МДС F определить требуемый магнитный поток Ф. Из точки Um=Um1+Um2=F проводим прямую Ф=(F-U1m)/Rm2 для зазора, из начала координат- нелинейную зависимость Ф(Um1) и из условия постоянства магнитного потока по всей магнитной цепи Ф=const в точке пересечения А находим искомый магнитный поток в последовательной цепи Электромагнитные устройства: трансформаторы Трансформатор-это устройство для преобразования одного переменного напряжения в другое той же частоты. Он имеет не менее двух обмоток с общим магнитным потоком, которые электрически изолированы друг от друга. Магнитопровод изготовлен из электротехнической стали для усиления индуктивной связи и снижения потерь от вихревых токов (для частот менее 20 кГц).
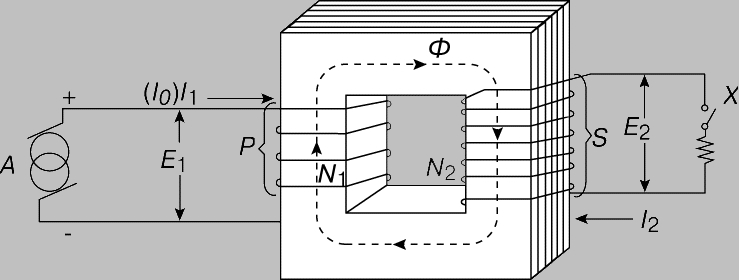
Рис. 1. ТРАНСФОРМАТОР. Схема устройства. Обозначения на схемах.
На щитке трансформатора указываются: Напряжение низшее (НН)и высшее(ВН). Номинальная полная мощность (В А или кВ А). Ток при номинальной полной мощности. Частота, число фаз, схема соединений и способ охлаждения. Если первичное напряжение Е1 меньше вторичного -работа в режиме повы
|

 =Ам sin(ω t+ψ) -
=Ам sin(ω t+ψ) -  =Am ejψ , Amej(ω t+ψ)=Amcos(ω t+ψ)+j Am sin(ω t+ψ)
=Am ejψ , Amej(ω t+ψ)=Amcos(ω t+ψ)+j Am sin(ω t+ψ)
 равна синусоидальной величине изменения тока. В плоскости J +1 проекция вектора
равна синусоидальной величине изменения тока. В плоскости J +1 проекция вектора 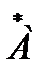 на ось OJ предстаёт в синусоидальном виде.
на ось OJ предстаёт в синусоидальном виде. =Iejψ =I< ψ,
=Iejψ =I< ψ,
 , φ =arctg((XL-XC)/R), I=U/Z ej(ψ u-φ).
, φ =arctg((XL-XC)/R), I=U/Z ej(ψ u-φ).
 )=U I cosφ [ВТ], -активная мощность.
)=U I cosφ [ВТ], -активная мощность.
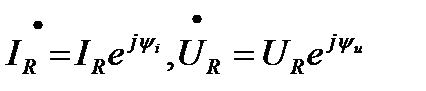
 -ЗАКОН ОМА для резистора
-ЗАКОН ОМА для резистора

 закон Ома для индуктивности
закон Ома для индуктивности -Закон Ома для емкости
-Закон Ома для емкости


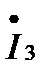










 (закон Ома для малых приращений);
(закон Ома для малых приращений);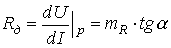 -дифференциальное сопротивление.
-дифференциальное сопротивление. ;
; .
.
 -магнитодвижущая сила (МДС)-[Ампер]
-магнитодвижущая сила (МДС)-[Ампер]



 =Um1+Um2=Iω =F,
=Um1+Um2=Iω =F,