Схема- графическое изображение электрической цепи.
Контур- замкнутый путь тока.
Схема замещения позволяет описать процессы, происходящие в эл.
цепи.
Законы электрических цепей.
Законы Кирхгофа.
1.Закон для любого узла
 -
-
2.Закон для любого замкнутого контура
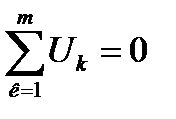
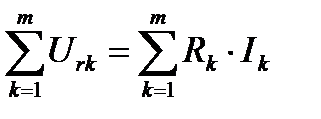 =
= 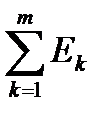
I1 I2
Расчёт электрических цепей.

-I
1-I
2+I
3=0
R1 I1+R3 I3=E1+E3
R2 I2+R3 I3=E2+E3
Из системы трёх уравнений находим неизвестные токи I1, I2, I3.
В цепи последовательно соединенных резисторов эквивалентное сопротивление R=Σ Ri
I1=(U1-U2)/R1 I2=(U1-U2)/R2 I1/I2=R2/R1
I=(U1-U2)/R 1/R=1/R1+1/R2
В цепи параллельно соединенных резисторов эквивалентная проводимость цепи G=1/R равна сумме проводимостей G=Σ Gi.
Метод эквивалентного преобразования схем
Предыдущая схема может быть упрощена и заменена эквивалентной
эквивалентной: ток I=(U1-U2)/R, 1/R=1/R1+1/R2
1/R= 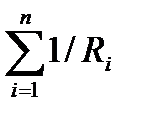 —эквивалентная проводимость в параллельной цепи сопротивлений (R-эквивалентное сопротивление). В последовательной цепи сопротивление R=
—эквивалентная проводимость в параллельной цепи сопротивлений (R-эквивалентное сопротивление). В последовательной цепи сопротивление R= 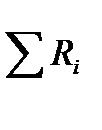 .
.
Принцип эквивалентности состоит в том, что после замены части сложной схемы на эквивалентную- режим работы остальной части схемы не изменится.
Метод контурных токов.
Метод позволяет уменьшить число решаемых уравнений до числа независимых контуров.
1.выбираем в каждом из контуров положительное направление токов по часовой стрелке.
Для каждого из трёх контуров составляем уравнения по 2 закону Кирхгофа
Контур 1: I11 (R1+R6+R4)-R6 I22+R4 I33=E1-E4
Контур 2: -I11 R6+I22 (R2+R5+R6)+I33 R5=E2,
Контур 3: I11 R4+I22 R5+I33 (R3+R4+R5)=E3-E4.
Из системы трёх уравнений находим токи I11, I22, I33.
По первому закону Кирхгофа находим токи ветвей:
I1=I11, I2=I22, I3=I33, I4=-I11-I33, I5=I22+I33, I6=I11-I22.
Соединение сопротивлений по схеме звезда и треугольник
Треугольник Звезда
Треугольник.
Проводимость между узлами АБ.
1/RAB+1/(Rca+RBC)=(RAB+RСА+RBC)/(RAB(RCA+RBC))=1/R
Cопротивление между А и Б равно: R=(RAB(RCA+RBC))/(RAB+RСА+RBC)
Звезда: сопротивление между АВ согласно условию эквивалентности
RA+RB=(RAB (RBC+ RCA))/(RAB+RBC+RCA)
RB+RC=(RBC (RCA+RAB))/(RAB+RBC+RCA)
RC+RA=(RCA (RAB+RCA))/(RAB+RBC+RCA)
Откуда:
RA=RAB RCA/(RAB+RBC+RCA),
RB=RBC RAB/(RAB+RBC+RCA)
RC=RCA RBC/(RAB+RBC+RCA)
При равенстве сопротивлений RAB=RBC=RCA=R сопротивления всех ветвей эквивалентной звезды Rзв =Rтреуг /3.
Возможно и обратное преобразование звезды в треугольник:
RAB=RA+RB+RA RB/RC, RBC=RB+RC+RB RC/RA, RCA=RC+RA+RC RA/RB.
Условие передачи приемнику максимальной энергии.
Мощность приёмника: PH=RH I2=(EEK-REK I) I=RH EEK2/(RH+REK)2.
Мощность источника ЭДС: PE=EEK I=(RH+REK) I2.
КПД передачи энергии: η =PH/PE=RH/(RH+REK)=1-REK I/EEK
Максимум мощности приёмника: dPH/dRH=E2EK[(RH+REK)2-RH 2 (RH+REK)]/(RH+REK)4=0
(RH+REK)2-2 RH2-2 RH REK=0, -RH2+REK2=0, RH=REK
PHmax=EEK2/4/RH-условие максимальной мощности.


 -
-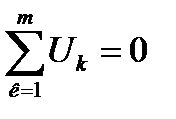
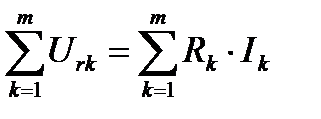 =
= 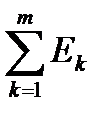
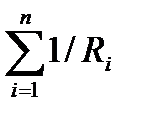 —эквивалентная проводимость в параллельной цепи сопротивлений (R-эквивалентное сопротивление). В последовательной цепи сопротивление R=
—эквивалентная проводимость в параллельной цепи сопротивлений (R-эквивалентное сопротивление). В последовательной цепи сопротивление R= 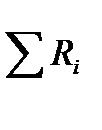 .
.


