ЭНЕРГЕТИЧЕСКИЕ ПАРАМЕТРЫ ОИ
ЭНЕРГЕТИЧЕСКИЕ ПАРАМЕТРЫ ОИ
Основные формульные зависимости Телесный угол
При При малых
Сила излучения
Поток ОИ Освещенность поверхности
Светимость поверхности
Связь светимости с освещенностью Яркость поверхности
Диффузные источники Задача 1
Определить полный поток излучения от диффузного (равнояркого) круглого диска с яркостью
Индикатриса силы излучения – симметричная относительно угла
Поток в оптическую систему, расположенную под углом
Задача 2 Определить силу излучения и полный поток излучения от диффузного (равнояркого) шара с яркостью
Силу излучения в вертикальном направлении (по вертикальной оси, относительно которой задан угол
Сила излучения равнояркого шара такая же как и у круглого равнояркого диска в направлении нормали, но потоки излучения разные, т.к. у шара – сила излучения постоянна, а у диска изменяется по Поэтому для шара можно сразу написать
Тот же результат получим путем интегрирования: поток в полусферу
полный поток
Задача 3
Площадь элементарной площадки поверхности цилиндра
Каждая элементарная площадка наклонена к нормали поверхности цилиндра под углом Найдем силу излучения (по известной яркости
Таким образом, сила излучения равнояркого цилиндра диаметром
Поток излучения в оптическую систему, расположенную под углом
Полный поток (во все стороны) излучения от равнояркого цилиндра получим при интегрировании по углу до
Задача 4
Диффузный объект освещается лазерным излучением передающей ОС мощностью Определить поток излучения, попадающий в приемную ОС с Угол между осями визирования
Площадь освещенной поверхности объекта
Освещенность объекта
Светимость объекта с коэффициентом отражения
Яркость диффузного объекта
Так как угловые поля передающей и приемной систем равны, то площадь, видимая приемной системой и освещенная площадь равны: Сила излучения от этой площадки равна
Поток излучения, собираемый ОС на ПИ
При
Задача 5
Найти распределение освещенности в изображении объекта в проходящем свете – диапроекция. Источник излучения – точечный с равной силой излучения во всех направлениях.
Сила излучения точечного источника излучения во всех направлениях одинакова (индикатриса силы излучения – сфера с центром в точечном источнике).
Освещенность осевой точки изображения равна
Освещенность крайней точки изображения
Например,
Задача 6 Найти распределение освещенности в плоскости изображения диффузного объекта - эпипроекция.
|






 ,
, 

 ;
;
 ;
; ,
,  ;
; ;
; ,
, 



 ;
; 
 и поток излучения в оптическую систему с диаметром зрачка
и поток излучения в оптическую систему с диаметром зрачка  , расположенную на расстоянии
, расположенную на расстоянии  от диска под углом
от диска под углом  к нормали излучающего диска.
к нормали излучающего диска.

 сила излучения по нормали к диску.
сила излучения по нормали к диску.
 .
.








 .
.

 до
до  (т.к. индикатриса симметричная) и по углу
(т.к. индикатриса симметричная) и по углу  , т.к. вклад яркости в силу излучения дают площадки от полусферы):
, т.к. вклад яркости в силу излучения дают площадки от полусферы):


 .
.



 Определить полный поток излучения от диффузного (равнояркого) цилиндра высотой
Определить полный поток излучения от диффузного (равнояркого) цилиндра высотой  и диаметром
и диаметром  с яркостью
с яркостью 
 до
до  .
. ) по нормали к излучающей поверхности от всех элементарных площадок, т.е. интегрируем по
) по нормали к излучающей поверхности от всех элементарных площадок, т.е. интегрируем по 

 и высотой
и высотой 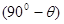 к нормали поверхности цилиндра (при малом телесном угле в пределах малого телесного угла силу излучения можно считать постлянной):
к нормали поверхности цилиндра (при малом телесном угле в пределах малого телесного угла силу излучения можно считать постлянной):
 :
:



 с угловой расходимостью
с угловой расходимостью  расположенной на расстоянии
расположенной на расстоянии  .
. , расположенную на том же расстоянии
, расположенную на том же расстоянии  .
. пренебрежимо мал.
пренебрежимо мал.
 .
.






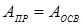













 .
.
 . Коллектив преобразует направление силы излучения, но при этом в каждой точки микрофильма сила излучения постоянна и равна
. Коллектив преобразует направление силы излучения, но при этом в каждой точки микрофильма сила излучения постоянна и равна 
 равна
равна
 .
.




