Кинематический анализ
Шестеренчатый дифференциал. У многих автомобилей сила тяги по двигателю обеспечивает движение в самых тяжелых условиях. Поэтому предельные тяговые свойства определяются сцеплением колес с дорогой. В зависимости от типа дифференциала предельная сила тяги по сцеплению существенно меняется. Пользуясь обычными для зубчатых планетарных механизмов методами, определим кинематические связи между его звеньями. Тогда внутреннее передаточное число (кинематический параметр) Р = Zj Z2 = («-(д )/(«-(Д ), (6.1) где z1, z2 - числа зубьев полуосевых шестерен, «, Ю2, Юд - угловые скорости полуосевых шестерен и корпуса дифференциала. Из (6.1) следует Ю - Р(= (1 - р)Юд. (6.2) Если кинематический параметр р = -1, т.е. z1 = z2, то дифференциал симметричный. Если кинематический параметр р = 1, то дифференциал несимметричный. Для симметричного дифференциала (= 2ЮД, (6.3) Из условия равновесия соотношение внешних моментов и мощностей, приложенных к дифференциалу, МД = M 1 + Ы2, N1 + N2 = Кд -Nr или М(+ М(2 = МдЮД - Nr, где М1, М2, N1, N2 - соответственно моменты и мощности, отведенные от дифференциала, Мд, Nд - соответственно, момент и мощность, приложенные к дифференциалу, Nr - мощность, затраченная на трение в дифференциале Nr = Мг(«2-ЮД) = 0, 5Mr(2 - (). Тогда Мх = ^2(Мд + Мг), М2 = 2(МД - Мг) Полуось, имеющая меньшую угловую скорость, называется отстающей, а с большей скоростью - забегающей. Для симметричного дифференциала
где кб - коэффициент блокировки дифференциала
M,, M„ - M3 k6 = Mд MO + M3 Здесь Mo, M3 - моменты, соответственно, на отстающей и забегающей полуосях. При отсутствии потерь на трение в дифференциале, т.е. Mr = 0, коэффициент блокировки кб = 0, поэтому крутящий момент распределяется поровну между полуосями. Если момент трения в дифференциале Mr = Mд, то дифференциал будет полностью заблокирован и коэффициент блокировки кб = 1. При отсутствии блокировки дифференциала предельная сила тяги автомобиля по сцеплению без буксования одного из колес может быть достигнута лишь при одинаковых величинах коэффициента сцепления с дорогой ф под всеми ведущими колесами. Однако, для того, чтобы использовать полностью силу сцепления ведущих колес с грунтом даже при весьма значительной разнице в коэффициентах сцеплениях ф под отдельными колесами, необходимость иметь полностью заблокированный дифференциал с кб = 1 отсутствует.
Определим максимальное значение величины коэффициента блокировки кб. С этой целью подставим в (6.6) значения Mo и M3 для практически возможной разницы в коэффициенте ф (рис 6.4). Тогда коэффициент блокировки для автомобиля с колесной формулой 4 х 2 при равенстве нагрузок на правое и левое колеса k = 0, 5Z2 rk (Ф тах -ffmrn) = 0? g 6 0, 5 Z2 rk (Ф тах +Ф шт) '. Более высокие значения коэффициента блокировки k6 не улучшают тяговых свойств автомобиля. С другой стороны, значительная разница в фтах и фтт встречается довольно редко, поэтому обычно ограничиваются величиной k6 = 0, 3...0, 5. При этом следует помнить, что более высокие значения существенно ухудшают управляемость, способствуют усиленному износу шин, а на скользких дорогах - заносу. Рассмотрим влияние дифференциала на тяговые свойства автомобиля с колесной формулой 4х 2. Для этого рассмотрим три возможных случая. 1. Межосевой дифференциал отсутствует (блокированный привод), межколесные дифференциалы заблокированы. Предельная сила тяги по сцеплению P = + КппФг + КзёФз + КпфА, где RZij - вертикальная реакция дороги на соответствующее колесо, например, RZm - переднее левое, ф, - коэффициент сцепления с дорогой для отдельного колеса. 2. Межосевой дифференциал отсутствует, межколесный дифференциал заблокирован k6 = 0. Предельная сила тяги по сцеплению PT21 = (RZnn + RZnn )ф12тш + (RZ3n + RZ3n )ф34тт, где ф12т.п - минимальное значение коэффициента сцепления из ф и ф2. 3. Межосевой и межколесный дифференциалы заблокированы k6 = 0. Предельная сила тяги по сцеплению P = (RZnn + RZnn + RZ3M + RZ3n )ф1234тш, где ф1234т.п - минимальное значение коэффициента сцепления из четырех значений ф. Очевидно, что PT, > PT2 > PT3. КПД передачи связан с коэффициентом блокировки дифференциала зависимостью , B M - M. л B, п = i—(——-) = 1—h, 2 R Mo + M/ 2 R б' где B - колея ведущих колес автомобиля, R - радиус поворота центра ведущей оси автомобиля. Таким образом, КПД передачи является переменной величиной и зависит от радиуса поворота автомобиля. Изменение кб от 0, 1 до 0, 5 соответствует изменению КПД от 0, 99 до 0, 95 при соотношении B / 2R = 0, 1.
Кулачковый дифференциал. Кулачковый дифференциал относится к дифференциалам с повышенным внутренним трением и выполняется с радиальным и осевым расположением кулачков (рис. 6.5).
Рис 6.5. Схемы кулачкового дифференциала а - с радиальным расположением кулачков; б - с осевым расположением кулачков
Сухари могут размещаться в один или два ряда. При однорядном размещении число кулачков на полуосевых элементах (звездочках) должно быть разным, при этом хотя бы один из сухарей будет передавать усилие. При двухрядном размещении число кулачков (рис.6.6) одинаково, но один ряд сухарей относительно другого смещают на половину шага кулачков. Кулачки внутренней звездочки 2, связанной с одной из полуосей, также расположены в два ряда, со смещением на половину шага. С другой полуосью связана наружная звездочка 3, кулачки которой выполнены по всей ширине звездочки. Ведущим элементом является корпус дифференциала 1 с обоймой 4, в отверстиях которой могут перемещаться в радиальном направлении сухари 5. Такая конструкция позволяет всегда иметь в зацеплении один ряд сухарей, т.е. передавать усилие одновременно всеми сухарями одного из рядов.
Для того, чтобы выявить кинематические свойства кулачкового дифференциала рассмотрим элементарную схему (рис 6.7). На схеме обозначено: vR - линейная скорость обоймы корпуса дифференциала, vJies и vnpae - линейные скорости звездочек, соответственно, левой и правой полуосей.
Пусть Vnpais > vM > Vnm, аёев = аправ, тогда относительная скорость звездочки левой полуоси V = Vrr — V лев Д пев Относительная скорость звездочки правой полуоси V = V — Vn
прав прав Д Есёи аправ = алев , то V„pm = VJleв , ПРи этом v +v =2v„ лев прав Д По структуре приведенное равенство не отличается от кинематического уравнения симметричного дифференциала, поэтому свойства кулачкового с одинаковым профилем кулачков звездочек и шестеренного симметричного дифференциала аналогичны. Если углы наклона алев и аправ не равны, что характерно для однорядного кулачкового дифференциала с неравным числом кулачков, уравнение кинематики дифференциала будет иметь следующий вид:
v + v = 2v„ — (v
лев прав Д \.
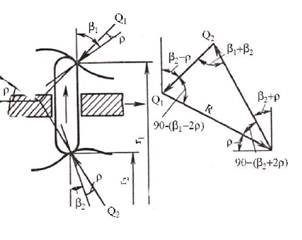
В этом случае кулачковый дифференциал несимметричный. Определим динамические свойства кулачкового дифференциала (рис. 6.8). На кулачках отстающей полуоси скорость скольжения сухаря направлена в сторону вращения ведущего элемента, а на кулачках забегающей полуоси - в противоположную сторону. Вследствие этого силы трения между сухарями и поверхностями кулачков увеличивают момент, передаваемый на отстающую полуось, и уменьшают момент, передаваемый на забегающую полуось. Рис.6.8
Со стороны кулачков забегающей (внешней) и отстающей (внутренней) звездочек на сухарь действуют силы Qx и Q2, дающие результирующую реакцию R, действующую на сухарь со стороны обоймы корпуса дифференциала. Силы Qj и Q2 направлены под углом трения р к общей нормали Моменты на забегающей и отстающей полуосях мз = Pr1 = Q^sin^ -р), Mo = P2 r2 = Q2 Г2^п(А +P), где r1 и r2 - расстояния от точек контакта ползуна с внутренним и наружным кулачками до оси вращения. Коэффициент блокировки дифференциала k = мo - M = Q2 r 2 sin (e2 + Р) - Q i r sin (A - р) (610) 6 M0 + M3 Q 2 ^т(А + р) + Qr sin (A -р)' ^ Из треугольника сил (рис.6.5) по теореме синусов Q1 = Q2 sin(e2 + 2р) cos(e - 2р). Тогда Q2 = G[cos(A - 2р)/ cos(^2 + 2р)]. (6.11) Подставив зависимость (6.11) в выражение (6.10), получим k= cos(А - 2р) sin(e2 + р)г2 - cos(e2 + 2р) sin(e1 - р)г1 (612) 6 cos(A - 2р)sin(в2 + р)г2 + cos(^2 + 2р)sin(вl -р)г1.. При двухрядном расположении сухарей углы в и в2 обычно равны между собой, что обеспечивает независимость коэффициента блокировки от того, какое из колес является отстающим или забегающим.
|



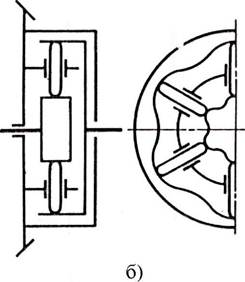
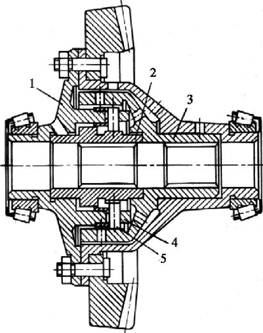 Рис.6.6. Двухрядный кулачковый дифференциал
Рис.6.6. Двухрядный кулачковый дифференциал
 Рис. 6.7. Кинематическая схема кулачкового дифференицала
Рис. 6.7. Кинематическая схема кулачкового дифференицала