Теория метода и описание прибора. Плоское движение совершает маятник Максвелла, который представляет собой диск, насаженный на тонкий стержень и подвешенный на двух нитях
Плоское движение совершает маятник Максвелла, который представляет собой диск, насаженный на тонкий стержень и подвешенный на двух нитях, закрепленных на оси диска (см. рис. 4.3). Нить накручивается на ось диска. При раскручивании нити диск спускается, вращаясь вокруг своей оси. Плоское движение диска можно рассматривать как сумму поступательного движения оси вращения АВ и вращательного движения диска вокруг неподвижной оси АВ. Поэтому для описания движения маятника Максвелла воспользуемся основными уравнениями динамики: поступательного движения
где и вращательного движения
где
На ось действуют две силы – сила натяжения нити
Для решения этой системы уравнений воспользуемся связью между тангенциальной составляющей ускорения и угловым ускорением
Из этого выражения видно, что маятник Максвелла будет двигаться равноускоренно. Если учесть, что маятник опускается с высоты без начальной скорости, то
тогда из выражения (4.25) следует
Следовательно, по этой формуле мы сможем определить момент инерции маятника Максвелла. Момент инерции однородного диска и цилиндра относительно оси, проходящей через ось симметрии цилиндра, можно определить также по формуле
где m1 – масса цилиндрического тела, R1 – его радиус. Используя формулу (4.28), можно легко получить формулу для моментов инерции полых цилиндрических тел:
где R2 – внешний, R1 – внутренний радиус полого цилиндра. Момент инерции нескольких тел равен сумме моментов инерции каждого тела в отдельности. Следовательно, момент инерции маятника Максвелла JP равен сумме моментов инерции диска JD, кольца JK и оси JO: JP = JO + JD +JK. Тогда для момента инерции маятника Максвелла можно получить расчетную формулу
где mO – масса оси, mD – масса диска, mK – масса кольца, RD – радиус диска, RK – внешний радиус кольца, RO – радиус оси. Маятник, поднятый на высоту
При падении маятника происходит изменение его потенциальной и кинетической энергии так, что полная механическая энергия остается постоянной согласно закону сохранения механической энергии:
Изменение потенциальной энергии маятника
где m – масса маятника, h – высота падения. Изменение его кинетической энергии
где
По закону сохранения энергии
|

 , (4.22)
, (4.22) – результирующая всех сил, действующих на тело массой m;
– результирующая всех сил, действующих на тело массой m;  – его ускорение;
– его ускорение; , (4.23)
, (4.23)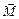 – результирующий момент всех сил, действующих на тело с моментом инерции J;
– результирующий момент всех сил, действующих на тело с моментом инерции J;  – его угловое ускорение.
– его угловое ускорение. Рис.4.3
Рис.4.3
 (маятник висит на двух нитях) и сила тяжести
(маятник висит на двух нитях) и сила тяжести  , где
, где  – суммарная масса диска и оси. Следовательно,
– суммарная масса диска и оси. Следовательно,  . Сила натяжения нити
. Сила натяжения нити 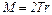 , где r – радиус осевого стержня. Тогда уравнения в проекциях на ось ОХ и на ось вращения АВ соответственно имеют вид
, где r – радиус осевого стержня. Тогда уравнения в проекциях на ось ОХ и на ось вращения АВ соответственно имеют вид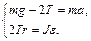 (4.24)
(4.24) . Тогда для момента инерции маятника Максвелла мы получаем выражение
. Тогда для момента инерции маятника Максвелла мы получаем выражение . (4.25)
. (4.25) , (4.26)
, (4.26) . (4.27).
. (4.27). , (4.28)
, (4.28)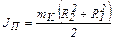 , (4.29)
, (4.29)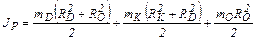 , (4.30)
, (4.30) , обладает потенциальной энергией
, обладает потенциальной энергией  . При скатывании маятник одновременно движется поступательно и вращается относительно оси, поэтому его кинетическая энергия
. При скатывании маятник одновременно движется поступательно и вращается относительно оси, поэтому его кинетическая энергия . (4.31)
. (4.31)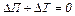 ,
,  . (4.32)
. (4.32) , (4.33)
, (4.33) , (4.34)
, (4.34) (D – диаметр оси маятника),
(D – диаметр оси маятника),  ; следовательно,
; следовательно, . (4.35)
. (4.35)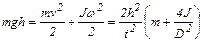 . (4.36)
. (4.36)


