Задача №1. Эпюра Mвер приведена на рисунке 16 г
2.9 Задача 9. Расчет сжатых стержней на устойчивость
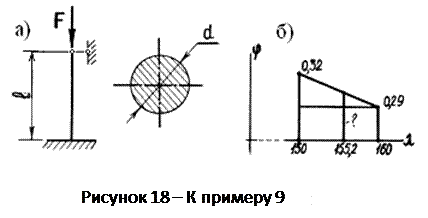
Стержень (материал – сталь Cт.3) длиной l сжимается силой F (рисунок 17). Требуется: а) из расчета на устойчивость по коэффициенту снижения основного допускаемого напряжения определить размеры поперечного сечения стержня, приняв [s] = 160 Мпа; б) определить значения критической силы Fкр и коэффициента запаса устойчивости nу. Данные взять из таблицы 9. Таблица 9
Указания. Задача 9 является задачей на тему «Продольный изгиб» (или «Расчет сжатых стержней на устойчивость»). Поскольку рассматриваемая задача является задачей проектного расчета, то из условия устойчивости следует выразить геометрический фактор поперечного сечения. Но поскольку коэффициент снижения основного допускаемого напряжения в свою очередь зависит от размеров и формы поперечного сечения, то приходится, задаваясь его значениями, искать решение с помощью последовательных приближений. Пример 9. Подобрать из условия устойчивости диаметр стойки круглого поперечного сечения, нагруженной, как показано на рисунке 18 а. Определить значения критической силы Fкр и коэффициента запаса устойчивости nу. Дано: F = 30 кН; l = 2, 4 м; [s] = 160 МПа (материал стойки – сталь Ст.3). Решение. Условие устойчивости для сжатых стержней имеет вид где [s] - основное допускаемое напряжение на сжатие; A – площадь поперечного сечения стержня. Первое приближение. Зададимся значением А = Так как поперечное сечение стержня представляет собой круг, то его площадь отсюда
где Imin- минимальный осевой момент инерции сечения. Для круга так что
Подставляя числовые значения, получаем Гибкость стержня где Для стержня с жесткой заделкой на одном конце и шарнирным закреплением на другом Тогда Обращаясь к таблице X.I [4, с. 272], находим, что для значений гибкости, больших 200, значения Второе приближение. Зададимся значением По таблице X.I [4] имеем для стали Ст.3 при при Находим с помощью линейной интерполяции (рисунок 18 б) значение
Очевидно, что значение Третье приближение. Зададимся значением Тогда По таблице X.I [4] имеем при при
Находим с помощью линейной интерполяции значение
Как видно, значения Недогрузка составляет что вполне приемлемо. Так как в рассматриваемом случае Подставляя числовые значения, получаем Коэффициент запаса устойчивости определяем, как
1. Теоретическая механика: Методические указания и контрольные задания для студентов-заочников энергетических, горных… специальностей вузов /Под ред. С.М.Тарга. – М.: Высш. шк., 1988. 2. Прикладная механика: Методические указания и контрольные задания /Под ред. П.Г.Гузенкова. – М.: Высш. шк., 1982. 3. Тарг С.М. Краткий курс теоретической механики. - М.: Высш. шк., 1986. 4. Степин П.А. Сопротивление материалов. - М.: Высш. шк., 1988. 5. Буланов Э.А. Решение задач по сопротивлению материалов. – М.: Высш. шк., 1994. 6. Пособие к решению задач по сопротивлению материалов /Миролюбов И.Н. и др. – М.: Высш.шк., 1985. 7. Степин П.А. Сопротивление материалов. - М.: Высш. шк., 1988. 8. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. - М.: Высш. шк., 2003. 9. Аркуша А.И. Техническая механика. Руководство к решению задач по теоретической механике. - М.: Высш. шк., 2002. 10. Расчетные и курсовые работы по сопротивлению материалов /Ф.З.Алмаметов, С.И.Арсеньев, С.А.Енгалычев и др. – М.: Высш.шк., 1992.
Алмас Даменович Динасылов
МЕХАНИКА Методические указания и задания к расчетно-графическим работам для студентов специальностей 050718 – Электроэнергетика, 050702 – Автоматизация и управление, 050717 – Теплоэнергетика
Подписано в печать.. 2006 г. Бумага типографская N 1 Тираж 150 экз. Заказ Формат 70х100 1/16 Цена 105 тг. Объем 2, 6 уч.-изд. л.
Копировально-множительная лаборатория Алматинского института энергетики и связи 050013, Алматы, Байтурсынова, 126
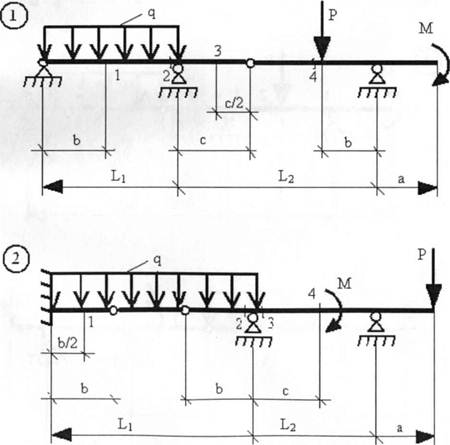
Задача №1
Задание: для балки, выбранной согласно варианту (стр.3-6), требуется: a) Построить эпюры М и Q (аналитически); b) Построить линии влияния М и Q для заданного сечения, а также линию влияния одной опорной реакции (по выбору студента); c) Определить по линиям влияния М, Q и R от заданной нагрузки.
Дано: L1=13м, q=2, 2kH/m, Ь=2м, L2=6m, P=2, 8kH, сечение№4, схема 2, а=1, 2м, с=2, 2м, М=2, 2кНм.
Решение; Строим эпюры изгибающих моментов М и поперечных сил Q. Для наглядного представления о работе заданной многопролётной балки изобразим схему взаимодействия отдельных элементов балки - " поэтажную" схему. После построения " поэтажной" схемы, заданную балку можно
Стоим эпюры M и Q Сечение 1: Q(
Определяем
Определяем опорные реакции:
9.9*2+2.2*2-2.2+6* 19.8+4.4-2.2+6* 24.2-22.36+6* 6*
Реактивная сила имеет противоположное направление.
-2.8*1.2-2.2+9.9*8+2.2*2*7= -3.36-2.2+79.2+30.8=
Проверка:
- -17.41+17.41=0 Сечение 1:
M( Сечение2:
M( M( Сечение 3:
M( M( Сечение 4: Q( Q(
M(
Строим эпюры Q и M, рассматривая балку АВ со свободного конца:
Q(
M( Строим линии влияния Линия влияния Линия влияния строится в два этапа. На первом этапе строится линия влияния искомого усилия в пределах той отдельной балки, к которой относится исследуемая опора (или усилие). На втором этапе добавляется продолжение линии влияния, обусловленное взаимодействием отдельных балок.
По балке ДЕ груз Р=1. Определяем величину опорной реакции
Этим уравнением устанавливается закон изменения величины реакции Изобразив этот закон графически, получим линию влияния опорной реакции
При х=0 Ординаты х/6 линии влияния опорной реакции величины отвлеченные.
При x=7.2m При x=-2m Когда груз Р=1 находится в точке С, опорная реакция
Поперечная сила, действующая в сечении 4, равна алгебраической сумме проекций внешних сил, взятых слева либо справа отсечения 4, на нормаль к оси балки. Рассмотрим два положения груза Р=1. 1. Груз расположен правее сечения 4. Рассматриваем левую часть балки ДЕ.
Для построения графика этого уравнения вычислим два значения
При x=2.2m При x=6m 2. Груз расположен левее сечения 4. Рассматриваем правую часть балки ДЕ.
Вычисляем два значения: При x=0
При х=2, 2m По этим данным строим праву и левую прямее лини влияния Давление балки ВС на балку ДЕ передается через шарнир С. Давление на шарнир С, при движении Р=1 по элементу ВС меняется по линейному закону: при Р=, расположенному в шарнире С, оно равно единице, а в шарнире В – нулю. Поэтому линию влияния
Линия влияния м4 Изгибающий момент, действующий в сечении 4, равен алгебраической сумме моментов внешних сил справа и слева от сечения относительно центра тяжести данного сечения. Знак моментов берётся так же, как при построении эпюры М. Р=1 находится левее сечения 4, х < 2, 2м, рассматриваем правую часть балки ДЕ, на которой имеется только реакция RE и момент в сечении 4 равен: M4=Re'3, 8 Следовательно, линия влияния М4 может быть получена из линии влияния RE путём умножения ординат последней на 3, 8. Подставив значение реакции RE, получим М4= х 3, 8 Построим график этого уравнения: При х=0 М4=0 При х=2, 2м М4=1, 393 По этим данным строим прямую, называемую левой прямой линии влияния М4; её ординаты дают значения изгибающего момента в сечении 4, когда груз Р=1 расположен слева этого сечения. Когда Р=1 расположен правее сечения 4, для определения изгибающего момента в сечении, удобнее рассматривать левую часть балки ДЕ
Для построения графика этого уравнения достаточно вычислить два значения
При x=2.2m При x=6m По этим данным строим прямую, называемую правой прямой линии влияния Значения характерных ординат находится из подобия треугольников.
S== S- искомое усилие
tg
|

 ,
, - коэффициент снижения основного допускаемого напряжения;
- коэффициент снижения основного допускаемого напряжения;
 м2.
м2. ;
;
 м.
м.

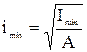 ,
,
 ,
, .
.
 м.
м.
 ,
, - коэффициент приведения длины стержня, зависящий от способа его закрепления.
- коэффициент приведения длины стержня, зависящий от способа его закрепления. .
. = 0, 25 и повторим расчет. Тогда
= 0, 25 и повторим расчет. Тогда
 м2,
м2, =
=  м,
м, м,
м, .
. =150
=150  :
: .
. .
. .
.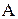
 м2,
м2,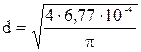 =
=  м,
м,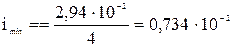 м,
м, .
.

 и
и  близки. Проверим, достигнута ли сходимость расчета, для чего сопоставим расчетные напряжения сжатия
близки. Проверим, достигнута ли сходимость расчета, для чего сопоставим расчетные напряжения сжатия  с допускаемыми напряжениями по условию устойчивости [
с допускаемыми напряжениями по условию устойчивости [  МПа,
МПа, МПа.
МПа. ,
, , значение которого для стали Ст.3 равно 100, критическую силу определяем по формуле Эйлера (в противном случае следовало бы воспользоваться эмпирической формулой Ясинского)
, значение которого для стали Ст.3 равно 100, критическую силу определяем по формуле Эйлера (в противном случае следовало бы воспользоваться эмпирической формулой Ясинского) или
или 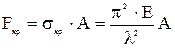 .
. 0, 0488 МН = 48, 8 кН.
0, 0488 МН = 48, 8 кН. .
.




 , m
, m
 , m
, m



 =
=  +q
+q  , 0< =
, 0< =  =
=  ; M(
; M( =0
=0 : x=
: x=  =
=  =4.5m;
=4.5m; =9.9*4.5-2.2
=9.9*4.5-2.2  =44.55-22.275=2.275kH/m
=44.55-22.275=2.275kH/m
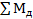 =0
=0  *6-P*7.2=0
*6-P*7.2=0 =0 -P*1.2-M-
=0 -P*1.2-M-  *6+q+2+7=0
*6+q+2+7=0 =0
=0 =-P+
=-P+  =-P(
=-P( +1.2)-
+1.2)-  =P+
=P+  (
( -M; 0< =
-M; 0< = 
 )=-2.8*5-0.31*3.8*2.2=-17.378kHm
)=-2.8*5-0.31*3.8*2.2=-17.378kHm )=-2.8*7.2-0.31*6-2.2=-24.2kHm
)=-2.8*7.2-0.31*6-2.2=-24.2kHm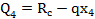 ; 0< =
; 0< = 
 )= -
)= - 
 )=-9.9-2.2*2=-14.3kH
)=-9.9-2.2*2=-14.3kH


 +q
+q 
 )-
)-  =9.9kH; Q(
=9.9kH; Q( )=9.9+2.2*2=14.3kH
)=9.9+2.2*2=14.3kH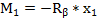 -q
-q 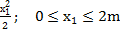
 )=-9.9*2-2.2
)=-9.9*2-2.2 
 ,
, 


 в зависимости от расстояния х. Для этого возьмем сумму моментов всех сил относительно левой опоры:
в зависимости от расстояния х. Для этого возьмем сумму моментов всех сил относительно левой опоры:
 т.к. Р=1
т.к. Р=1 . Так как переменная входит в уравнение в первой степени, то линия влияния будет прямолинейной.
. Так как переменная входит в уравнение в первой степени, то линия влияния будет прямолинейной.


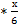 . Следовательно линия влияния
. Следовательно линия влияния 

 :
:





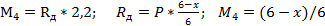 *2.2
*2.2
 *2.2=1.393
*2.2=1.393 +
+  +
+ 
 - сосредоточенная сила, действующая на балку
- сосредоточенная сила, действующая на балку - ордината линии влияния под силой
- ордината линии влияния под силой 
 - распределенная нагрузка
- распределенная нагрузка - площадь участка линии влияния под равномерно распределенной нагрузкой
- площадь участка линии влияния под равномерно распределенной нагрузкой - изгибающий момент
- изгибающий момент - тангенс угла наклона прямолинейного участка линии влияния.
- тангенс угла наклона прямолинейного участка линии влияния. -3.927-0.733+0.367+3.36=0.31kH
-3.927-0.733+0.367+3.36=0.31kH





