Тақырып: Үздіксіз басқару жүйелерін математикалық өрнектеуҚ арастырылатын сұ рақ тар: 1. Автоматты басқ ару жү йелерінің (АБЖ) функционалдық сү лбасы. 2. Жү йелердің беріліс функциялары туралы тү сініктер.
Дә рістің қ ысқ аша жазбасы: Автоматты басқ ару жү йесі қ ұ рылымы жағ ынан ә р тү рлі болуы ық тимал. Жалпы жағ дайда бұ л кұ рылымғ а белгілі бір ерекше қ асиеттерімен жә не аралық ә сер беру жолдарымен жіктелген автоматты жү йені тү зетін дербес бө ліктердің жиынтығ ы жатады. Автоматты басқ ару жү йесінің функционалдық қ ұ рылымында ә рбір бө лік белгілі бір қ ызметті атқ арады. Қ ызмет ретінде автоматты басқ арушы қ ұ рылғ ының ақ парат алу, оны ө ң деу, т. б. осы секілді негізгі қ ызметін, сонымен бірге сигналды беру, оларды салыстыру, ақ паратты беру тү рін ө згерту тә різді дербес қ ызметін айтуга болады. Басқ ару жү йесінің қ ұ рылымын график бойынша кескіндеуді қ ұ рылымдық сұ лба дейді. Белгілі бір ерекшеліктерімен топталган автоматты жү йе бө лігін график тү рінде, ішінде бұ л жү йенің оның кандай бө лігі екендігін білдіретін шартты белгісі бар тө ртбұ рышпен кескіндейді. Автоматты жү йенің бө ліктерінің арасында берілетін ә сер жолын, сол ә сер берілетін бағ ыт бойымен бағ ыттауыш сызық пен кескіндейді. Автоматты басқ ару жү йесінің, не автоматты қ ұ рылғ ының қ ұ рылымдық схемасындағ ы бө ліктері арасындағ ы берілетін ә сердің бағ ыты мен жолын кө рсететін қ арапайым қ ұ рамдас бө лігін қ ұ рылымдық сұ лбаның байланысы деп атайды. Автоматты жү йенің қ ұ рылымдық сұ лбасының байланысы негізгі, қ осымша жә не кері байланыстар болып ажыратылады. Мысал ретінде 2.1-суретте басқ ару объектісінен (БО), басқ арушы (БҚ), жә не салыстырушы (СҚ) қ ұ рылғ ысынан тұ ратын автоматты басқ ару жү йесінің қ арапайым қ ұ рылымдық сұ лбасы кө рсетілген. Автоматты басқ ару жү йесінің кірісі жә не шығ ысы болады. Кіріс деп, сырттан жү йеге не қ ұ рылғ ығ а, оның жеке бө ліктеріне тікелей ә сер берілетін автоматты басқ ару жү йесінің ә сер тізбегінің бө лігін айтады. 2.1-суретте ә сер беру тізбегінің бір бө лігі жү йенің g(t) жоспарлау ә сері берілетін кірісі де, екінші бө лігі f(t) қ оздыру ә сері берілетін кірісі. Шығ ыс деп, автоматты жү йеде не оның элементтерінде қ ызмет алгоритміне сә йкес қ алыптасқ ан ә серді сырт жақ қ а беретін автоматты басқ ару жү йесінің ә сер тізбігінің бө лігін айтады. 2.1 суретте X автоматты басқ ару жү йесінің шығ ысы.
2.1-сурет Автоматты басқ ару жү йесінің ә сер тізбегі деп ішкі жә не сыртқ ы ә серлер берілетін жеке жолдардың жиынтығ ын айтады. Қ ұ рылымдық сұ лбада ә сер тізбегінің жеке жолдары тұ тас жә не бағ ыттауыш сызық тармен кескінделеді. Автоматты басқ ару жү йесінің не оның қ арастырылатын бө лігінің шартты тү рде бө лінген, кірісінен шығ ысына қ арай бағ ытталғ ан ә сер тізбегін жү йенің негізгі ә сер тізбегі деп атайды. Автоматты басқ ару жү йелерді қ ұ ру ү шін зерттелетін объектілерді алгебралық жә не дифференциал тең деулермен ө рнектеу қ ажет. Тең деулердің статика не орнық қ ан режим тең деулері жә не динамика не ө тпелі процесс тең деулері тә різді екі тү рі бар. Статика тең деулері жоспарланғ ан ә сердің тұ рақ ты болуына қ арай, ә детте алгебралық болып табылады, ал динамика тең деулері ә детте дифференциалды. Олар ауытқ ыту кү шінің ә серінен туатын ө тпелі процесс кезіндегі, не олар аяқ талғ аннан кейінгі жү йенің қ алпын айқ ындайды. Динамика тең деуін жасау ү шін автоматты жү йе жеке буындарғ а ажыратылып, олардың ә рқ айсысы ү шін сол буында ө тетін процеске тә н физикалық заң негізіне сә йкес тең деулер қ ұ рылады. Автоматты жү йенің барлық элементтері ү шін қ ұ рылғ ан динамика тең деулерінің жиынтығ ы автоматты басқ ару процесін анық тайды.
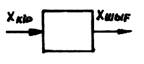
2.2-сурет
Буындарда ө тетін процестерді айқ ындайтын физикалық заң дар негізіне автоматты басқ ару жү йесі буындарының динамикасының тең деулерін жасау автоматты жү йені есептеуде ең басты мә селе, ө йткені бастапқ ы шартта жіберілген дә лсіздік кейінгі есептеулерді жоқ қ а шығ аруы мү мкін. Ал, ө неркә сіптегі болатын процестердің сан алуан болатындығ ынан жоғ арыда айтылғ андай буындардың динамика тең деулерін қ ұ рудан баска жалпы нұ сқ ау беру мү мкін емес. Ә р жағ дайда нақ ты ө неркә сіптік қ ондырғ ы ү шін дербес тә сіл қ олданғ ан қ ажет. хкір арқ ылы элементар буынның кірісіне ық пал ететін физикалық шаманы, ал хшығ арқ ылы сол буынның шығ ыстық параметрін белгілесек (2.2-сурет), онда буынның дифференциал тең деуі жалпы тү рде мынандай болады:
мұ ндағ ы аі жә не bі — тұ рақ ты коэффициенттер. Егер осы тең деуін бастапқ ы нө лдік шартты ескере отырып Лаплас бойынша тү рлендірсек, онда ол мына тү рге келеді: xшығ (р)(а0рn+а1рn-1+...+аn)=хкір(р)(b0рm+b1pm-1+...+bm) (2.2) не қ ысқ арғ ан тү рде: N(р)хшығ (t)=М(р)хкір(t). (2.3) Басқ арудың автоматты жү йесіндегі буынның беріліс функциясы деп, нө лдік бастапқ ы шарттардағ ы шығ ыстық пен кірістік шамалардың арасындағ ы Лаплас бойынша ө рнектелген кескіндерінің қ атынасын айтады. Айталық нө лдік бастапқ ы шартта Лаплас бойынша тү рленген (2.1) буынның тең деуі мынадай болады: хшығ (р)(а0рn+а1рn-1+...+аn)=хкір(р)(b0рm+b1pm-1+...+bm), (2.4) немесе
Осыдан алынғ ан
шамасын буынның беріліс функциясы дейді. К(р) мен Q(р) — р комплекс айнымалының полиномдары. К(р)=b0рm+b1рm-1+...+bm, Q(р)=а0рn+а1рn-1+...+аn. Беріліс функциясы ұ ғ ымы автоматты басқ ару жү йесін ү йлестіру жә не есептеуде инженерлік есептерді шешуді едә уір оң айлатады. Айталық, жү йенің беріліс функциясын біле отырып жә не (2.5) шығ ыстық шаманы ескере отырып, Лапластың кері тү рлендіруі бойынша жү йедегі ө тпелі процесті табуғ а болады: хшығ (t)=L-1[xкір W(р)].(2.6) Жү йенің беріліс функциясын ө з кезегінде қ арапайым буындарының беріліс функциялары бойынша есептейді. Ол ү шін ә р бө лігі (буыны) қ ызметтің қ арапайым алгоритмін орындайтын жү йенің алгоритмдік қ ұ рылымдық сұ лбасын қ ұ рады. Бө лікті жү йенің алгоритмдік қ ұ рылымдық сұ лбасында ішінде беріліс функциясы кө рсетілген тіктө ртбұ рыш тү рінде бейнелейді. Автоматты жү йелерде буындар ә ртү рлі байланыста бола алады. Осығ ан қ арамастан кү рделілігі ә ртү рлі жү йені ә рқ ашан жай бу-ындардың ү ш тү рі тізбекті, параллель жә не қ арсы-параллель қ осылысы тү рінде қ арастыруғ а болады. Бақ ылау сұ рақ тары: 1. Функционалдық сұ лба деген не? 2. Қ ұ рылымдық сұ лба деген не? 3. Қ ұ рылымдық сұ лбаның байланысы деген не? 4. Негізгі ә сер тізбегі деген не? 5. Буынның беріліс функциясы деген не? 6. Жү йенің беріліс функциясы деген не?
|
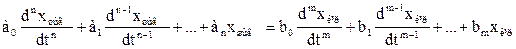, (2.1)
. (2.5)
