Тақырып: Автоматты басқару жүйелерінің орнықтылығы

Қ арастырылатын сұ рақ тар:

1. Орнық тылық туралы тү сініктер.

2. Михайлов жә не Найквистің жиіліктік критерийлары.

 

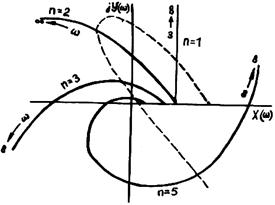
Дә рістің қ ысқ аша жазбасы:

Жұ мыс істеп турғ ан автоматты жү йеге ә ртү рлі тұ рақ ты сыртқ ы қ озулар ә сер етуі салдарынан реттелетін шығ ыстық шаманың мә ні жиі ө згеріп отырады. Жү йенің автоматты реттеуіші осы реттелетін шаманы берілген мә нге келтіруге ұ мтылады. Бірақ тұ тастай алғ анда жү йеде инерциялық массалар, реактивті элементтер (индуктивтік, сыйымдылық) болатындық тан, оның орнық ты қ алпына келуі, немесе қ алыптасқ ан бір кү йден келесісіне ө туі лезде емес, белгілі тү рде кешігіп жү зеге асады. Жү йеде ө тпелі процесс туындайды. Бұ л жағ дайда, егер жү йе қ озу ә рекеті тоқ талғ аннан кейін қ алыптасқ ан кү йге оралса, ол орнық ты. Егер оралмаса, онда ор-нық сыз. Орнық сыз жұ мыс кері байланыспен қ амтылғ ан АРЖ-ның барлығ ында туындауы ық тимал.

АРЖ-ның орнық тылығ ын анық тау мә селесі басты болып саналады, ө йткені орнық сыз жү йелер іс жү зінде жарамсыз. Орнық тылық ты зерттеудің жалпы ә дісі АРЖ-ның g(t) жоспарлау (басқ арушы) жә не f(t) қ оздыру ә серлері тудыратын у(t) реттелетін шаманың ө згеруі ү шін жазылғ ан

(а₀рⁿ+ а₁р^n-1+...+а_n) у(t)=(b₀р^m+b₁р^m-1+...+b_m) g(t) (3.1)

дифференциал тең деуін талдаумен тұ жырымдалады.

АРЖ-ның орнық тылығ ын ә детте орнық тылық критерийлерімен бағ алайды. Орнық тылық тың негізгі Раус-Гурвиц, Михайлов жә не Найквист критерийлері секілді ү ш критерийі бар.

Михайлов критерийі. Бұ л критерийді А. В. Михайлов 1938 жылы жариялағ ан. Ол сызық ты тұ йық талғ ан автоматты реттеу жү йелерін зерттеуге арналғ ан. Автоматты жү йелердің орнық тылығ ын анық тау жү йенің си­паттамалық тең деуін талдауғ а негізделген. Осы тең деудін р_і белгілі тү бірлерінде, оны былай жазуғ а болады:

а₀(р-p₁)(р-p₂)...(p-р_n)=0. (3.2)

(3.2)-дегі р-ны jω -мен алмастырсақ, онда

G(jω) = а₀(jω -p₁)(jω -p₂)...(jω -р_n). (3.3)

G(jω) сипаттамалық векторды ә р (jω -p_i) кө бейткіші комплекс сан болып табылады. ω 0-дан ∞ -ке дейін ө згерген кезде, G(jω) сипаттамалық векторды қ ұ райтын векторлардың ұ шы жорамал ось бойымен φ _i(ω) аргументті (фазаң ы) ө згерте отырып, ығ ысады. Егер тү бір нақ ты сандар бойында жорамал осьтің сол жағ ында орналасса, онда ω ө згерісі кезінде (jω -p_i) векторы сағ ат тілінің бағ ытына қ арсы бұ ралады, оның аргументі оң, ал шекті мә ні π /2-ге тең

1іm аrg(jω -p_i)=π /2,

егер тү бір оң жақ та орналасса, онда

1іm аrg(jω -p_i)=-π /2.

Барлық тү бірлері жорамал осьтің сол жағ ында орналасатын орнық ты жү йеге сә йкес келетін G(jω) вектор­дың аргументі мынағ ан тең:

аrg G(jω)=nπ /2; 0< ω < ∞. (3.4)

ω жиілігінің ө згеруіне сә йкес G(jω) векторының шамасы мен бағ ыты да ө згеріп отырып, оның ұ шымен қ айсыбір қ исық (годограф) сызылады, оны Михайлов го­дографы дейді. Комплексті айнымалы жазық тығ ында орналасатын бұ л қ исық тың тү рі бойынша орнық ты ма, жоқ па екенін анық тайды.

Михайлов кисығ ын салу ү шін (3.5) сипаттамалық тең деуіндегі р-ның орнына jω -ны қ ояды да

G(jω)=а₀(jω)ⁿ+a₁(jω)^n-1+...+a_n=0, (3.6)

G(jω) векторын нақ ты жә не жорамал бө ліктер тү рінде кө рсетеді

G(jω)=Х(ω)+jY(ω), (3.7)

мұ ндағ ы X(ω)=а_n-a_n-2ω ²+a_n-4ω ⁴-... (3.8)

Y(ω)=а_n-1-a_n-3ω ³+a_n-5ω ⁵-.... (3.9)

ω -ғ а 0-ден ∞ -ке дейінгі аралық та ә ртү рлі мә ндер бере отырып, X(ω) мен Y(ω)-ның бірқ атар шамасын алады, ол G(jω) векторының ұ шының координаттарын білдіреді. Осы нү ктелерді ө зара қ осу арқ ылы Михайлов годографын аламыз. Бұ л қ исық ω =0 кезінде ә рқ ашан оң нақ ты осьте X(ω)=а_n, Y(ω)=0 нү ктесінде басталун тиіс, ал (3.4) шартын сақ тау ү шін қ исық жазық тық тың n квадрантын сағ ат тілінің бағ ытына қ арсы біртіндеп, координат басын баспай ө туі тиіс.

Егер зерттелетін жү йе орнық сыз болса, онда бұ рылыстың қ орытқ ы бұ рышы nπ /2-ден кем болып, годог­раф n квадрантты басып ө тпейді.

3.1-суретте ү зік сызық пен орнық сыз жү йенің Михайлов годографы кө рсетілген, ө йткені ол квадранттың бірінен (ү шіншісінен) ө тпейді.

 

3.1-сурет

 

Орнық ты жү йе ү шін n-ші квадрантта қ исық шексіздікке кетуі тиіс, ө йткені тек осы жағ дайда ғ ана (3.4) шарты орындалады. Сонымен Михайлов орнық тылығ ының критерийі былай ө рнектеледі: егер n-ші ретті АРЖ орнық ты болса, онда сипаттамалық вектор ω 0-ден ∞ -ке дейін ө згергенде nπ /2 бұ рышқ а бұ рылуы тиіс, немесе ω 0-ден ∞ -ке дейін ө згергенде Михайлов годографы оң нақ ты жарты осьтен басталып комплексті жазық тық тың n квадранттар санын сағ ат тілінің бағ ытына қ арсы кезектеп ө туі тиіс.

Найквист критерийі. Бұ л критерийдің жә рдемімен ажыратылғ ан жү йенін амплитудалық -фазалық -жиіліктік сипаттамасының тү рі бойынша тұ йық талғ ан жү йенің орнық тылығ ын бағ алауғ а болады. Осы критерий қ азір оң айлығ ы, кө рнекілігі жә не тә жірибе жасауғ а мү мкіншілік туғ ызуына байланысты кең тарағ ан.

Найквист критерийінің жә рдемімен автоматты жү йенің орнық тылығ ын тә жірибе арқ ылы зерттегенде ондағ ы кері байланысты ү зеді. Жү йенің кірісіне амплитудасы Х_m мен жиілігі ω х=Х_mе^{jω t} тұ рақ ты тербеліс беріледі. Сызық тық жү йе арқ ылы ө ткен сигналдың жү йенің шығ ысындағ ы жиілігі де сондай, ал амплитудасы мен фазасы ө згеше болады:

у=Y_mе^{j(ω t+φ )}.

Комплексті беріліс коэффициенті немесе жиіліктік беріліс функциясы бұ лай анық талады

W(jω)=[Y_m(ω)/X_m(ω)]e^{jφ (ω t)}=A(ω)e^{jφ (ω t)}. (3.10)

А(ω) мен φ (ω) мә ндері жиілікке тә уелді. W(jω) жиіліктік беріліс функциясын ω ө згергенде комплекс айнымалылар жазық тығ ында осы вектордың годографы, яғ ни амплитудалық -фазалық сипаттама (АФС) тү рінде кескіндеуге болады.

Зерттелетін ашық жү йенің беріліс функциясын біле отырып жә не ондағ ы р операторды jω -ғ а алмастырып, жиіліктік беріліс функциясын немесе амплитудалық -фазалық -жиіліктік сипаттаманы (АФС) алады. Тә жірибе жү зінде не есептеумен алынғ ан АФС-ның тү рі бойынша жү йе орнық ты ма, жоқ па, соны анық тайды.

Орнық тылық тың Найквист критерийі былайша тұ жырымдалады: егер тұ йық талмағ ан кү йдегі АРЖ орнық ты болса, онда ол тұ йық талғ ан кү йде де орнық ты болуы ү шін тұ йық талмағ ан жү йенің амплитудалық -фа-залық сипаттамасы координаты (-1, j0) нү ктені қ амтымауы қ ажетті ә рі жеткілікті.

Орнық тылық тың қ арастырылғ ан тұ жырымы тұ йық талмағ ан жү йе орнық ты болып, АФС тең деуіндегі бө лшектің алымындағ ы полином дә режесі бө ліміндегі полином дә режесінен кем болғ анда ғ ана дұ рыс болады.

Тұ йық талмағ ан жү йе орнық ты жә не бейтарап буындардан қ ұ ралғ анда ғ ана орнық ты болады. Бұ л жү йенің қ ұ рылымдық сұ лбасынан қ ұ ралғ ан буындар қ ұ рамын қ арастырғ анда тағ айындалады.

АФС координаты (-1, j0) нү ктені қ амти ма, жоқ па, соны анық тау ү шін осы нү ктеден АФС-ның барлық нү ктелеріне вектор тұ рғ ызылады. Егер жү йе орнық ты болса, онда [1+W(jω)] векторының қ орытқ ы бұ рылысы (3.2, а-сурет, 1-қ исық) нө лге тең. Ал орнық сыз жү йе ү шін ол нө лге тең болмайды (3.2, б-сурет, 1-қ исық). Бұ л бұ рыш 2π -те тең.

3.2-сурет

 

Бақ ылау сұ рақ тары:

1. Орнық тылық деген не?

2. Раус критерийінің анық мамасын берініз.

3. Гурвиц критерийінің анық мамасын берініз.

4. Михайлов критерийінің анық мамасын берініз.

5. Найквист критерийінің анық мамасын берініз.