Тақырып: Автоматика релелері мен логикалық элементтері
Қ арастырылатын сұ рақ тар: 1. Автоматика релелерінің жіктелуі. 2. Релелік сұ лбалар теориясынан жә не олардың салдарынан жалпы мағ лұ маттар.
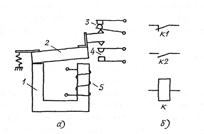
Дә рістің қ ысқ аша жазбасы: Реле деп белгілі-бір мө лшерлі физикалық шаманың ә серінің нә тижесінде екінші-бір жү йенің кү йін секірмелі ө згертуге арналғ ан аспапты айтады. Реле ә ртү рлі салада ә ртү рлі қ ызмет атқ арады. Электрлік релелердің кө пшілігі электромагниттен жә не тұ йық таушы һ ә м ажыратушы тү йіспелерден тұ рады (7.1-сурет). Егер шарғ ығ а (5) кернеу берсе, онда ө зекте магнит ерісі қ оздырылады. Магнит ө рісінің ә рекетінен якорь (2) ө зекке (1) тартылып, ажыратушы тү йіскілер (3) ажырайды да, тү йық таушы тү йіспелер (4) тұ йық талады. Релені іске қ осатын, яғ ни якорьді ө зекке тартып тұ ратын кү ш тудыратын, ә сер етуші шаманың минимал мә нін реленің іске қ осылу параметрі деп атайды. Реле қ айтатын, яғ ни якорьді ө зекке тартып ұ стап тұ ра алмайтын, ә сер етуші шаманың максимал мә нін реленің босату параметрі деп атайды.
7.1-сурет. Электромагниттік реленің қ ұ рылысы (а) жә не тү йіспелер мен шарғ ының шартты белгілері (б).
Реленің босату параметрінің Хб іске қ осылу параметріне Хік Қ атынасы реленің қ айтымдық коэффициенті деп аталады:
Қ айтымдық коэффициент неғ ұ рлым бірге жақ ын болса, соғ ұ рлым реленің дә лдігі жоғ ары болады деп есептеледі. Ә сер етуші шамағ а байланысты жә не арналымына қ арай релелер токтық, кернеулік, уақ ыттық, жиіліктік, арнаулы, т.с.с. больш бө лінеді. Мысалы, токтық реле электрлік қ ондырғ ыларды ток кү ші бойынша асқ ын жү ктелуден қ орғ ауғ а жә не токтың мә ніне байланысты басқ аруғ а арналғ ан. Токтық реленің іске қ осылу тоғ ын оның токтық ұ стамы деп атайды. Ә детте токтық реленің шарғ ысы арқ ылы бақ ылауғ а алынғ ан ток, яғ ни жү ктің тогы жү руі керек. Сондық тан реледегі кернеудің тү суі аз болуы ү шін токтық реленің шарғ ысы кедергісі аз жуан сымнан жасалады. Осындай релені кернеудің мә нін бақ ылау ү шін де қ олдануғ а болады. Бірақ кернеулік реленің шарғ ысы кернеуі бақ ыланатын элементке параллель жалғ анады. Сондық тан оның шарғ ысы кедергісі ү лкен, яғ ни орам саны кө п, жің ішке сымнан жасалғ ан болуы керек. Кө птеген қ ондырғ ылар мен қ ұ рылғ ылардың жұ мысы уақ ыт бойынша кезектілікті жә не сатылық ты қ ажет етеді. Ал оны қ амтамасыз ету ү шін басқ ару тізбектерінде уақ ыт релесі қ олданылады. Уақ ыт релесі ә ртү рлі ү рдіске негізделген (электромагниттік, электрондық, механикалық, т.с.с.), бірақ солардың ішінен сағ ат механизмін қ олданатын уақ ыт релесі кең тарағ ан. Автоматика жү йесінің қ азіргі дамуы ақ параттың ө ң деуінің жылдамдығ ы мен кө лемінің жоғ арлауымен, техникалық жабдық тардың іс дә лдігі мен сезгіштігінің ө суімен сипатталады. Бірақ та қ азіргі уақ ытта кең пайдаланылатын релелі-тү йіспелі аппаратура жаң а талаптарғ а сә йкес келмейді. Релелік-тү йіспелі аппаратураның орнына логикалық элементтер қ олданады. Логикалық элементтер элементтің кіріс жә не шығ ыс белгілері арасындағ ы логикалық тә уелділікті жү зеге асырады. Логикалық элементтердің талдау мен қ ұ растыру ү шін математикалық логика тә сілін пайдаланады - оны логика алгебрасы деп атайды. Логика алгебрасын Буль алгебрасы деп те атайды. Логикалық элементтердің кірмесі мен шық пасындағ ы кернеудің бары немесе жоғ арғ ы дең гейі «1» деп, ал оның жоғ ы немесе тө менгі дең гейі «0» деп алынады. Осы себепті де жоғ арыда аталғ ан қ ұ рылғ ыларда екілік санау жү йесі қ олданылады. Екілік санау жү йесін қ олдану «ЕМЕС», «ЖӘ НЕ», «НЕМЕСЕ» деп аталатын қ арапайым ү ш тү рлі тізбекті барлық логикалық жә не цифрлық қ ұ рылғ ылардың негізіне алуғ а мү мкіндік береді. Бульдік логикалық ө рнектерді жасау ү шін, 7.1 кестеде кө рсетілген небары ү ш негізгі оператор қ ажет.
7.1 кесте
Қ осу, немесе V таң басы логикалық НЕМЕСЕ ү шін қ олданылады; кә дімгі алгебрада кө бейту белгісі ретінде пайданылатын нү кте немесе ^ таң басы Буль алгебрасында логикалық ЖӘ НЕ ү шін қ олданылады. Логика алгебрасының қ арапайым ө рнегіне (7.1)-ін алуғ а болады, мұ нда Ү шығ ыстық (тә уелді) айнымалысы А жә не В екі кірістік (тә уелсіз) айнымалыларының функциясы болады: Ү =А·В (7.1) Бұ л ө рнек шығ ыстық айнымалысы ақ иқ ат болуы ү шін (логикалық бірлікке сә йкес келуі ү шін) – екі кірістік айнымалылары (А мен В) ақ иқ ат болулары керектігін (яғ ни бірлікке тең мә нге ие болуы) кө рсетеді. Ал ө рнекте тек бір қ осылғ ыш болғ андық тан, баламасы болмайды: тек А мен В-ның белгілі бір комбинацаясы Ү -тің нә тижесін бере алады. (7.2) ө рнегі Ү -тің шығ ысын алу ү шін балама жасайды: Ү =(А·В)+С. (7.2) Осы ө рнекке сә йкес Ү -тің шығ ысын А жә не В айнымалыларының мә ні бірге тең болмаса да, С айнымалысы бірге тең болғ анда бірлік мә нге ие болады. (7.2) ө рнегі “А жә не В немесе С“ деп оқ ылады да, (7.1) ө рнегіне қ арағ анда Ү шығ ыстық айнымалысының болуының онша қ атаң емес шартын кө рсетеді. ЕМЕС операторы тек қ ана ө рнек мә нін керісінше ө згертеді, яғ ни ол нө лге тең болса, онда ЕМЕС операторы ө рнекті бірге тең естіреді немесе керісінше жасайды. Бульдік ө рнектердегі жақ шалар кә дімгі алгебралық ө рнектердегі мағ ынаны береді. Алгебралық ө рнектерді жең ілдету. Буль алгебрасының теоремаларын қ алай пайдалануды кө рсетуді (7.3) ө рнегінің оң жағ ын тү рлендірудің мысалынан бастайық. Х=А·(В+ Бұ л ө рнектің сө збе-сө з мағ ынасы мынандай: Х шығ ысы бірге тең болады - ЕГЕР; 1. А кірісі бірге тең болса - ЖӘ НЕ; 2. В кірісі не бірге не нө лге тең болса. Осы мағ ынаны терең ірек қ арастырсақ, онда (7.3) ө рнегін барынша оң айлатуғ а болады. Логикалық айнымалы тек екі мә нді: 0 немесе 1-ді қ абылдайтынын еске салайық. Демек, В не бір не нө л бола алады. Бірақ (7.3) ө рнегінде (В+ Х=А (7.4) Бұ л ө рнектің мағ ынасы: А мә ні бірге тең болса, Х-те бірге тең; егер А нө л болса, Х-те нө л. Сонымен (7.3) ө рнегін бульдік алгебраның қ арапайым екі теоремасын пайдаланып оң айлаттық: 1) Қ осу (включение) теоремасы: В+ 2) Сипаттамалық теорема: А·1=А. Іс жү зінде логикалық ө рнектердің кө пшілігі (7.3)-не қ арағ анда ә лдеқ айда кү рделі, ә йтсе де олардың кө бін буль алгебрасының заң дары мен теоремаларына сү йеніп жең ілдетуге болады. Буль алгерасының жиі пайданылатын заң дары мен теоремалары 7.2 кестеде келтірілген Басқ а ғ ылымда да, кә дімгі алгебрада да, негізгі аксиомалар теоремаларды дә лелдеу ү шін қ ажет, ал олар ө з кезегінде басқ а теоремаларды немесе заң дарды дә лелдеуге пайдаланылады. Бір мысал келтірейік: Х+Х·Ү =Х жұ ту заң ын ДӘ ЛЕЛДЕУ керек. ДӘ ЛЕЛДЕМЕСІ: Х+Х·Ү =Х·1+Х·Ү =(сипаттамалық теорема негізінде)= =Х·(1+Ү)=(дистрибутивті заң негізінде)=Х·1=(сипаттамалық теорема негізінде)=Х (сипаттамалық теорема негізінде) Дә лелдейтініміз де осы еді. 7.2 кесте
Буль алгебрасын жете мең геру ү шін 7.2 кестесіндегі барлық теоремалар мен заң дарды дә лелдеп шығ у керек. Дегенмен ауыстырымдылық, терімділік, дистрибутивтік заң дары мен сипаттамалық, қ осу, идемпотенттік жә не терісті теріске шығ ару теоремалары кө кейге қ онымды, сол себептен де аксиома ретінде қ абылдануғ а тиісті. Кә дімгі алгебраның кө птеген негізгі заң дары буль алгебрасында да дә л сондай мағ ынада болатының оп-оң ай байқ ауғ а болады (мә селен, терімділік, ауыстырымдылық, дистрибутивтік заң дары). Сонда да кә дімгі алгебрадан алғ ан білімге ө те сене беруге де болмайды. Мысал ү шін 7.2 кестедегі сипаттамалық теореманың тө рт нұ сқ асын жете қ арастырып кө релік.Алғ ашқ ы ү ш нұ сқ а кә дімгі алгебрағ а ү йлесіп тұ рғ анымен, тө ртіншісі (Х+1=1) оның ережесіне қ айшы келеді. Сондық тан кә дімгі алгебраның ережелерін логика ө рнектеріне қ олданудың алдында, ол ережелер логика алгебрасына сай келер-келмейтіндігіне кө з жеткізіп алу керек. Буль алгебрасы логикалық ө рнектерді тек жазып қ ана қ оймай, оны оң ай тү рге келістіреді. Мұ ның ө зі басқ арудың ө неркә сіптік логикалық жү йесінің тиімділігі мен сенімділігін арттыруғ а бірден-бір жол ашады. Кезінде тек математикалық логика саласындағ ы мамандарғ а ғ ана таныс Буль алгебрасының логикалық операциялары электрондық есептеуіш машиналары пайда болғ аннан бастап техникалық салаларда кең інен қ олданылатын болды. Бақ ылау сұ рақ тары: 1. Реле деген не? 2. Автоматика релелерінің жіктеуі қ андай? 3. Электрлік реленің жұ мысы қ андай? 4. Реленің босату параметрі қ андай? 5. Реленің қ айтымдық коэффициенті қ андай? 6. Логика алгебрасы деген не? 7. Бульдік алгебраның теоремалары қ андай? 8. Бульдік алгебраның заң дары қ андай?
|

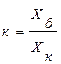



 ) (7.3)
) (7.3) )=Х
Қ осу (включение)теоремалары
1. Х·
)=Х
Қ осу (включение)теоремалары
1. Х·  =Х
2. (Х+Y)·(Х+
=Х
2. (Х+Y)·(Х+ 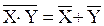 2.
2.