Тема: Кинематика поступательного и вращательного движения
Тема: Кинематика поступательного и вращательного движения
На рисунке представлены графики зависимости скорости четырех тел, движущихся прямолинейно, от времени.

Наибольшее перемещение за  совершено телом … 1) 3 2) 1 3) 2 4) 4
совершено телом … 1) 3 2) 1 3) 2 4) 4
Решение:
Перемещение тела совпадает по величине с расстоянием, пройденным телом за определенный промежуток времени, при движении по прямолинейной траектории без изменения направления движения и  . В данном случае интеграл вычислять не требуется, достаточно иметь в виду геометрический смысл интеграла. Наибольшее перемещение за
. В данном случае интеграл вычислять не требуется, достаточно иметь в виду геометрический смысл интеграла. Наибольшее перемещение за  совершено телом 3.
совершено телом 3.
Тема: Кинематика поступательного и вращательного движения
Тело движется с постоянной по величине скоростью по траектории, изображенной на рисунке:

Для величин полного ускорения а тела в точках А и В справедливо соотношение …
Решение: Величина полного ускорения определяется соотношением

, где

и

тангенциальное и нормальное ускорения соответственно, причем

,

, где
R – радиус кривизны траектории. Так как по условию скорость по величине постоянна, то тангенциальное ускорение всюду равно нулю. В то же время величина нормального ускорения в точке А больше, чем в точке В, поскольку радиус кривизны траектории в точке А меньше, чем в точке В, что видно из рисунка. Таким образом, величина полного ускорения в точке А больше, чем в точке В.
Тема: Кинематика поступательного и вращательного движения
Диск катится равномерно по горизонтальной поверхности со скоростью  без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
 1) 3 2) 1 3) 2 4) 4
1) 3 2) 1 3) 2 4) 4
Решение:
Качение однородного кругового цилиндра (диска) по плоскости является плоским движением. Плоское движение можно представить как совокупность двух движений: поступательного, происходящего со скоростью  центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда
центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда  . Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что
. Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что  . Вектор
. Вектор  направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости
направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости  точки А ориентирован в направлении 3.
точки А ориентирован в направлении 3.
Тема: Кинематика поступательного и вращательного движения
Точка М движется по спирали с равномерно возрастающей скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения точки …


|
| | увеличивается
|
|
|
| | уменьшается
|
|
|
| | не изменяется
|
|
|
| | равна нулю
|
Решение: Величина нормального ускорения определяется соотношением

, где
R – радиус кривизны траектории. По условию скорость возрастает, и в то же время кривизны траектории уменьшается, что видно из рисунка. Следовательно, величина нормального ускорения точки увеличивается.
Тема: Кинематика поступательного и вращательного движения
Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина тангенциального ускорения точки …


|
| | не изменяется
|
|
|
| | увеличивается
|
|
|
| | уменьшается
|
|
|
| | равна нулю
|
Решение:
Величина тангенциального ускорения определяется соотношением  . Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной.
. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной.
Тема: Кинематика поступательного и вращательного движения
Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …


|
| | Уменьшается
|
|
|
| | увеличивается
|
|
|
| | не изменяется
|
|
|
| | равна нулю
|
Решение:
Величина полного ускорения определяется соотношением  , где
, где 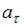 и
и  тангенциальное и нормальное ускорения соответственно, причем
тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается.
, где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается.
Тема: Кинематика поступательного и вращательного движения
Частица из состояния покоя начала двигаться по дуге окружности радиуса  с угловой скоростью, модуль которой изменяется с течением времени по закону
с угловой скоростью, модуль которой изменяется с течением времени по закону  . Отношение нормального ускорения к тангенциальному через 2 секунды равно … 1) 8 2) 4 3) 1 4) 2
. Отношение нормального ускорения к тангенциальному через 2 секунды равно … 1) 8 2) 4 3) 1 4) 2
Решение:
Нормальное ускорение частицы равно  , где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением
, где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением  . Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно
. Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно  .
.
Тема: Кинематика поступательного и вращательного движения
На рисунке представлен график зависимости угловой скорости  вращающегося тела от времени. Угловое ускорение тела (в
вращающегося тела от времени. Угловое ускорение тела (в  ) в промежутке времени
) в промежутке времени  равно… 1) 20 2) 10 3) 15 4) 5
равно… 1) 20 2) 10 3) 15 4) 5

Решение:
Из приведенного графика следует, что вращательное движение тела является равноускоренным. Поэтому угловое ускорение равно  .
.
Тема: Кинематика поступательного и вращательного движения
Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

При этом правильно изображает направление углового ускорения диска вектор … 1) 4 2) 1 3) 2 4) 3
Решение:
По определению угловое ускорение тела  , где
, где  – его угловая скорость. При вращении вокруг неподвижной оси векторы
– его угловая скорость. При вращении вокруг неподвижной оси векторы  и
и  коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора
коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора  связано с направлением вращения тела правилом правого винта. В данном случае вектор
связано с направлением вращения тела правилом правого винта. В данном случае вектор  ориентирован в направлении 4, и, так как после приложения силы движение становится ускоренным, вектор
ориентирован в направлении 4, и, так как после приложения силы движение становится ускоренным, вектор  ориентирован в направлении 4.
ориентирован в направлении 4.
Тема: Кинематика поступательного и вращательного движения
Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

До остановки диска правильно изображает направление угловой скорости вектор … 1) 4 2) 1 3) 2 4) 3
Решение:
Направление вектора угловой скорости  связано с направлением вращения тела правилом правого винта. В данном случае вектор
связано с направлением вращения тела правилом правого винта. В данном случае вектор  ориентирован в направлении 4. После приложения силы движение становится замедленным.
ориентирован в направлении 4. После приложения силы движение становится замедленным.
Тема: Кинематика поступательного и вращательного движения
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.

Угловое перемещение (в радианах) в промежутке времени от 4 с до 8 с равно … 1) 0 2) 2 3) 4 4) 8
Решение:
По определению  . Отсюда
. Отсюда  и
и  . Используя геометрический смысл интеграла, искомый угол поворота можно найти как площадь двух треугольников. При этом нужно учесть, что, во-первых, в момент времени
. Используя геометрический смысл интеграла, искомый угол поворота можно найти как площадь двух треугольников. При этом нужно учесть, что, во-первых, в момент времени  происходит изменение направления вращения тела на противоположное, и, во-вторых, площади треугольников равны. Поэтому угловое перемещение тела за рассматриваемый промежуток времени равно нулю.
происходит изменение направления вращения тела на противоположное, и, во-вторых, площади треугольников равны. Поэтому угловое перемещение тела за рассматриваемый промежуток времени равно нулю.
Тема: Кинематика поступательного и вращательного движения
Диск вращается вокруг своей оси, изменяя проекцию угловой скорости  так, как показано на рисунке. Вектор угловой скорости
так, как показано на рисунке. Вектор угловой скорости  и вектор углового ускорения
и вектор углового ускорения  направлены в одну сторону в интервалы времени …
направлены в одну сторону в интервалы времени …


|
| | от 0 до  и от и от  до до 
|
|
|
| | от 0 до  и от и от  до до 
|
|
|
| | от  до до  и от и от  до до 
|
|
|
| | от 0 до  и от и от  до до 
|
Решение: По определению угловое ускорение тела

, где

– его угловая скорость. При вращении вокруг неподвижной оси векторы

и

коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора

связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до

вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается, вектор углового ускорения направлен так же. В интервале времени от

до

вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается, следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.
Тема: Кинематика поступательного и вращательного движения
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике:

Через 11 с тело окажется повернутым относительно начального положения на угол _______  1) 0 2) 12 3) 24 4) 4
1) 0 2) 12 3) 24 4) 4
Решение:
По определению  . Отсюда
. Отсюда  и
и  . Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол
. Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол 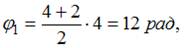 еще через 7 с – на угол
еще через 7 с – на угол  но в обратном направлении. Следовательно, через 11 с тело повернется на угол
но в обратном направлении. Следовательно, через 11 с тело повернется на угол 
 Тема: Кинематика поступательного и вращательного движения
Тема: Кинематика поступательного и вращательного движения
Диск радиуса R вращается с уменьшающейся по величине угловой скоростью вокруг вертикальной оси против часовой стрелки. Укажите направление вектора углового ускорения.
1) 6 2) 5 3) 3 4) 4
Решение:
При ускоренном вращении ( ) вектор углового ускорения сонаправлен с вектором угловой скорости; при замедленном вращении (
) вектор углового ускорения сонаправлен с вектором угловой скорости; при замедленном вращении ( ) вектор углового ускорения направлен противоположно вектору угловой скорости. Направление вектора угловой скорости связано с направлением вращения правилом правого винта. Таким образом, вектор
) вектор углового ускорения направлен противоположно вектору угловой скорости. Направление вектора угловой скорости связано с направлением вращения правилом правого винта. Таким образом, вектор  ориентирован в направлении 5, вектор
ориентирован в направлении 5, вектор  – в направлении 6.
– в направлении 6.
Тема: Динамика поступательного движения
Автомобиль поднимается в гору по участку дуги с постоянной по величине скоростью.

Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении …
Решение:
Согласно второму закону Ньютона 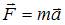 , где
, где  – равнодействующая всех сил, действующих на тело,
– равнодействующая всех сил, действующих на тело,  – его ускорение. Вектор ускорения удобно разложить на две составляющие:
– его ускорение. Вектор ускорения удобно разложить на две составляющие: 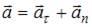 . Тангенциальное ускорение
. Тангенциальное ускорение  направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение
направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение 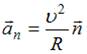 направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории
направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории  0, при движении с постоянной по величине скоростью
0, при движении с постоянной по величине скоростью  0. Следовательно, вектор
0. Следовательно, вектор  ориентирован в направлении 3. В этом же направлении ориентирован и вектор
ориентирован в направлении 3. В этом же направлении ориентирован и вектор 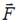 .
.
Тема: Динамика поступательного движения
Импульс тела  изменился под действием кратковременного удара и стал равным
изменился под действием кратковременного удара и стал равным  , как показано на рисунке:
, как показано на рисунке:

В момент удара сила действовала в направлении …
Решение:
Согласно второму закону Ньютона,  . Следовательно, вектор силы направлен так же, как разность импульсов
. Следовательно, вектор силы направлен так же, как разность импульсов 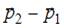 , то есть в направлении 2.
, то есть в направлении 2.
Тема: Динамика поступательного движения
Материальная точка движется под действием силы, изменяющейся по закону 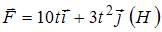 . В момент времени
. В момент времени  проекция импульса (в
проекция импульса (в  ) на ось ОХ равна …
) на ось ОХ равна …
Решение:
Согласно второму закону Ньютона, скорость изменения импульса материальной точки равна действующей на нее силе:  . В проекции на ось ОХ
. В проекции на ось ОХ  . Отсюда,
. Отсюда,  следовательно,
следовательно,  .
.
Тема: Динамика поступательного движения
Тело массой  движется с коэффициентом трения 0, 5 по наклонной плоскости, расположенной под углом
движется с коэффициентом трения 0, 5 по наклонной плоскости, расположенной под углом 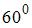 к горизонту. Сила трения (в
к горизонту. Сила трения (в  ) равна …
) равна …
Решение:
На тело, движущееся по наклонной плоскости, действует сила трения

Тема: Динамика поступательного движения
Механическая система состоит из трех частиц, массы которых  ,
, 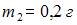 ,
,  . Первая частица находится в точке с координатами (2, 3, 0), вторая – в точке (2, 0, 1), третья – в точке (1, 1, 0) (координаты даны в сантиметрах). Тогда
. Первая частица находится в точке с координатами (2, 3, 0), вторая – в точке (2, 0, 1), третья – в точке (1, 1, 0) (координаты даны в сантиметрах). Тогда  – координата центра масс (в см) – равна …
– координата центра масс (в см) – равна …
Решение:
Центром масс системы материальных точек называется точка С, радиус-вектор которой определяется соотношением  .Тогда
.Тогда 
Тема: Динамика поступательного движения
Импульс материальной точки изменяется по закону  (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 1 c,
(кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 1 c,
равен …
Решение:
Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе:  . Тогда зависимость силы от времени имеет вид
. Тогда зависимость силы от времени имеет вид 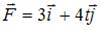 . Модуль силы
. Модуль силы  , и в момент времени t = 1 c
, и в момент времени t = 1 c
Тема: Динамика поступательного движения
Импульс материальной точки изменяется по закону:  . Модуль силы (в Н), действующей на точку в момент времени
. Модуль силы (в Н), действующей на точку в момент времени  , равен …
, равен …
Решение: Согласно второму закону Ньютона, скорость изменения импульса материальной точки равна действующей на нее силе:

. Тогда зависимость силы от времени имеет вид:

. Модуль силы

, и в момент времени

модуль силы равен

.
Тема: Динамика поступательного движения
Тело массой  движется равномерно по вогнутому мосту со скоростью
движется равномерно по вогнутому мосту со скоростью  . В нижней точке сила давления тела на мост вдвое превосходит силу тяжести. Радиус кривизны моста (в
. В нижней точке сила давления тела на мост вдвое превосходит силу тяжести. Радиус кривизны моста (в  ) равен …
) равен …
Решение:
Согласно второму закону Ньютона в нижней точке моста,  или
или  . Следовательно,
. Следовательно, 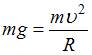 и
и 
Тема: Динамика поступательного движения
Вдоль оси OX навстречу друг другу движутся две частицы с массами m1 = 4 г и m2 = 2 г и скоростями V1 = 5 м/с и V2 = 4 м/с соответственно. Проекция скорости центра масс на ось ОХ (в единицах СИ) равна …

Решение:
Скорость центра масс механической системы равна отношению импульса системы к ее массе:  . Для рассматриваемой системы из двух частиц
. Для рассматриваемой системы из двух частиц  . Проекция скорости центра масс на ось ОХ
. Проекция скорости центра масс на ось ОХ 
Тема: Динамика поступательного движения
Система состоит из трех материальных точек массами 
 и
и  которые движутся так, как показано на рисунке.
которые движутся так, как показано на рисунке.

Если скорости шаров равны 

 то вектор скорости центра масс этой системы ориентирован …
то вектор скорости центра масс этой системы ориентирован …

|
| | в положительном направлении оси OX
|
|
|
| | в отрицательном направлении оси OX
|
|
|
| | в положительном направлении оси OY
|
|
|
| | в отрицательном направлении оси OY
|
Решение: Скорость центра масс механической системы равна отношению импульса системы к ее массе:

. Для рассматриваемой системы из трех частиц

. Проекция скорости центра масс на ось ОХ

, так как

. Проекция скорости центра масс на ось ОY равна

, так как

. Поэтому вектор скорости
центра масс этой системы ориентирован в положительном направлении оси OX.
Тема: Динамика поступательного движения
Под действием постоянной силы в  скорость тела изменялась с течением времени, как показано на графике:
скорость тела изменялась с течением времени, как показано на графике:

Масса тела (в 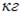 ) равна …
) равна …
Решение:
Из второго закона Ньютона 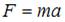 , где а – модуль ускорения, который можно найти из графика зависимости
, где а – модуль ускорения, который можно найти из графика зависимости  :
:  Тогда
Тогда 
Тема: Динамика поступательного движения
На рисунке приведен график зависимости скорости  тела от времени t.
тела от времени t.

Если масса тела 1, 5 кг, то изменение импульса тела (в единицах СИ) за первые 4 с движения равно …
Решение:
Изменение импульса равно:  . Изменение скорости
. Изменение скорости  в указанном временном интервале найдено из графика.
в указанном временном интервале найдено из графика.
Тема: Динамика поступательного движения
На рисунке приведен график зависимости скорости  тела от времени t.
тела от времени t.

Если масса тела равна 2 кг, то изменение импульса тела (в единицах СИ) за 2 с равно …
Решение:
Изменение импульса равно: 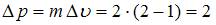 кг·м/с. Изменение скорости
кг·м/с. Изменение скорости  найдено из графика.
найдено из графика.
Тема: Динамика поступательного движения
На рисунке приведен график зависимости скорости тела  от времени t.
от времени t.

Масса тела 20 кг. Сила (в H), действующая на тело, равна …
Решение:
Из второго закона Ньютона  , где а – модуль ускорения, который можно найти из графика зависимости
, где а – модуль ускорения, который можно найти из графика зависимости  :
: 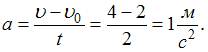 Тогда
Тогда 
Тема: Динамика поступательного движения
Мальчик тянет санки массой m по горизонтальной поверхности с ускорением  , при этом веревка натягивается силой
, при этом веревка натягивается силой  под углом
под углом  к горизонту. Если коэффициент трения полозьев о поверхность равен
к горизонту. Если коэффициент трения полозьев о поверхность равен 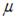 , то уравнение движения санок в проекции на направление движения санок имеет вид …
, то уравнение движения санок в проекции на направление движения санок имеет вид …
Решение:
Уравнение второго закона Ньютона в векторном виде имеет вид:  , где
, где 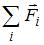 – векторная сумма всех сил, действующих на тело. Для данной задачи это уравнение запишется следующим образом:
– векторная сумма всех сил, действующих на тело. Для данной задачи это уравнение запишется следующим образом: 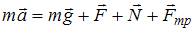 , где
, где  и
и  – сила реакции опоры и сила трения скольжения соответственно. Если ось OX направить по направлению движения, а ось OY – перпендикулярно ему, то уравнение второго закона Ньютона в проекциях на оси выбранной системы координат примет вид:
– сила реакции опоры и сила трения скольжения соответственно. Если ось OX направить по направлению движения, а ось OY – перпендикулярно ему, то уравнение второго закона Ньютона в проекциях на оси выбранной системы координат примет вид:  ,
,  . Выразив из второго уравнения
. Выразив из второго уравнения  и подставив полученное выражение в первое уравнение, получим
и подставив полученное выражение в первое уравнение, получим  .
.
Тема: Динамика вращательного движения
Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Зависимость момента импульса диска от времени представлена на рисунке линией …
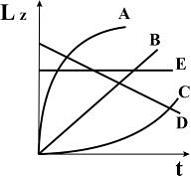

|
| | Е
|
|
|
| | A
|
|
|
| | B
|
|
|
| | C
|
|
|
| | D
|
Решение:
Момент импульса тела относительно неподвижной оси равен:  , где
, где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,  – угловая скорость. По условию диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Тогда
– угловая скорость. По условию диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Тогда  , то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией Е.
, то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией Е.
Тема: Динамика вращательного движения
Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. В некоторый момент времени на диск начинает действовать не изменяющийся со временем тормозящий момент. Зависимость момента импульса диска от времени, начиная с этого момента, представлена на рисунке линией …


|
| | D
|
|
|
| | A
|
|
|
| | B
|
|
|
| | C
|
|
|
| | E
|
Решение:
Момент импульса тела относительно неподвижной оси равен:  , где
, где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,  – угловая скорость. Так как по условию на диск, вращающийся с постоянной угловой скоростью, начинает действовать не изменяющийся со временем тормозящий момент, зависимость угловой скорости от времени имеет вид
– угловая скорость. Так как по условию на диск, вращающийся с постоянной угловой скоростью, начинает действовать не изменяющийся со временем тормозящий момент, зависимость угловой скорости от времени имеет вид  , где
, где  – угловое ускорение. Поскольку тормозящий момент не зависит от времени, то и
– угловое ускорение. Поскольку тормозящий момент не зависит от времени, то и  const. Тогда
const. Тогда  , то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией D.
, то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией D.
 Тема: Динамика вращательного движения
Тема: Динамика вращательного движения
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил ( ,
,  ,
,  или
или  ), лежащих в плоскости диска. Не создает вращающего момента относительно рассматриваемой оси сила …
), лежащих в плоскости диска. Не создает вращающего момента относительно рассматриваемой оси сила …
Решение:
При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения 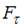 . Тогда момент силы относительно неподвижной оси равен:
. Тогда момент силы относительно неподвижной оси равен:  , где r – радиус-вектор точки приложения силы. В данном случае только для силы
, где r – радиус-вектор точки приложения силы. В данном случае только для силы 
 . Поэтому
. Поэтому  .
.
Тема: Динамика вращательного движения
К точке, лежащей на внешней поверхности диска, прикладывают четыре силы  ,
,  ,
,  и
и  , лежащих в плоскости диска. Если ось вращения проходит через центр О диска и перпендикулярна плоскости рисунка, то длина отрезка a является плечом силы …
, лежащих в плоскости диска. Если ось вращения проходит через центр О диска и перпендикулярна плоскости рисунка, то длина отрезка a является плечом силы …

Решение:
Плечо силы – это длина перпендикуляра, опущенного из точки О на линию действия силы. Из рисунка следует, что длина отрезка a является плечом силы  .
.

Тема: Динамика вращательного движения
Если ось вращения тонкостенного кругового цилиндра перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси _____ раза.

|
| | увеличится в 2
|
|
|
| | уменьшится в 2
|
|
|
| | увеличится в 1, 5
|
|
|
| | уменьшится в 1, 5
|
Решение:
Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно оси, проходящей через центр масс, вычисляется по формуле  . Момент инерции относительно оси, проходяще
. Момент инерции относительно оси, проходяще
 , где
, где  и
и  тангенциальное и нормальное ускорения соответственно, причем
тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Так как по условию скорость по величине постоянна, то тангенциальное ускорение всюду равно нулю. В то же время величина нормального ускорения в точке А больше, чем в точке В, поскольку радиус кривизны траектории в точке А меньше, чем в точке В, что видно из рисунка. Таким образом, величина полного ускорения в точке А больше, чем в точке В.
, где R – радиус кривизны траектории. Так как по условию скорость по величине постоянна, то тангенциальное ускорение всюду равно нулю. В то же время величина нормального ускорения в точке А больше, чем в точке В, поскольку радиус кривизны траектории в точке А меньше, чем в точке В, что видно из рисунка. Таким образом, величина полного ускорения в точке А больше, чем в точке В.
 , где R – радиус кривизны траектории. По условию скорость возрастает, и в то же время кривизны траектории уменьшается, что видно из рисунка. Следовательно, величина нормального ускорения точки увеличивается.
, где R – радиус кривизны траектории. По условию скорость возрастает, и в то же время кривизны траектории уменьшается, что видно из рисунка. Следовательно, величина нормального ускорения точки увеличивается.
 , где
, где  – его угловая скорость. При вращении вокруг неподвижной оси векторы
– его угловая скорость. При вращении вокруг неподвижной оси векторы  и
и  коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора
коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора  связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до
связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до  вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается, вектор углового ускорения направлен так же. В интервале времени от
вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается, вектор углового ускорения направлен так же. В интервале времени от  до
до  вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается, следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.
вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается, следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.
 . Тогда зависимость силы от времени имеет вид:
. Тогда зависимость силы от времени имеет вид:  . Модуль силы
. Модуль силы  , и в момент времени
, и в момент времени  модуль силы равен
модуль силы равен  .
.
 . Для рассматриваемой системы из трех частиц
. Для рассматриваемой системы из трех частиц  . Проекция скорости центра масс на ось ОХ
. Проекция скорости центра масс на ось ОХ  , так как
, так как  . Проекция скорости центра масс на ось ОY равна
. Проекция скорости центра масс на ось ОY равна  , так как
, так как  . Поэтому вектор скорости центра масс этой системы ориентирован в положительном направлении оси OX.
. Поэтому вектор скорости центра масс этой системы ориентирован в положительном направлении оси OX.


 совершено телом … 1) 3 2) 1 3) 2 4) 4
совершено телом … 1) 3 2) 1 3) 2 4) 4 . В данном случае интеграл вычислять не требуется, достаточно иметь в виду геометрический смысл интеграла. Наибольшее перемещение за
. В данном случае интеграл вычислять не требуется, достаточно иметь в виду геометрический смысл интеграла. Наибольшее перемещение за 


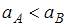

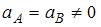
 без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении … 1) 3 2) 1 3) 2 4) 4
1) 3 2) 1 3) 2 4) 4 . Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что
. Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что  . Вектор
. Вектор  направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости
направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости  точки А ориентирован в направлении 3.
точки А ориентирован в направлении 3.

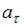 и
и  , где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается.
, где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается. с угловой скоростью, модуль которой изменяется с течением времени по закону
с угловой скоростью, модуль которой изменяется с течением времени по закону  . Отношение нормального ускорения к тангенциальному через 2 секунды равно … 1) 8 2) 4 3) 1 4) 2
. Отношение нормального ускорения к тангенциальному через 2 секунды равно … 1) 8 2) 4 3) 1 4) 2 , где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением
, где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением  . Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно
. Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно  .
. вращающегося тела от времени. Угловое ускорение тела (в
вращающегося тела от времени. Угловое ускорение тела (в  ) в промежутке времени
) в промежутке времени  равно… 1) 20 2) 10 3) 15 4) 5
равно… 1) 20 2) 10 3) 15 4) 5
 .
.
 – его угловая скорость. При вращении вокруг неподвижной оси векторы
– его угловая скорость. При вращении вокруг неподвижной оси векторы  коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора
коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора 

 . Отсюда
. Отсюда  и
и  . Используя геометрический смысл интеграла, искомый угол поворота можно найти как площадь двух треугольников. При этом нужно учесть, что, во-первых, в момент времени
. Используя геометрический смысл интеграла, искомый угол поворота можно найти как площадь двух треугольников. При этом нужно учесть, что, во-первых, в момент времени  происходит изменение направления вращения тела на противоположное, и, во-вторых, площади треугольников равны. Поэтому угловое перемещение тела за рассматриваемый промежуток времени равно нулю.
происходит изменение направления вращения тела на противоположное, и, во-вторых, площади треугольников равны. Поэтому угловое перемещение тела за рассматриваемый промежуток времени равно нулю. так, как показано на рисунке. Вектор угловой скорости
так, как показано на рисунке. Вектор угловой скорости  и вектор углового ускорения
и вектор углового ускорения  направлены в одну сторону в интервалы времени …
направлены в одну сторону в интервалы времени …
 до
до 
 и от
и от 

 1) 0 2) 12 3) 24 4) 4
1) 0 2) 12 3) 24 4) 4 . Отсюда
. Отсюда  и
и  . Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол
. Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол 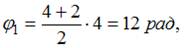 еще через 7 с – на угол
еще через 7 с – на угол  но в обратном направлении. Следовательно, через 11 с тело повернется на угол
но в обратном направлении. Следовательно, через 11 с тело повернется на угол 
 Тема: Кинематика поступательного и вращательного движения
Тема: Кинематика поступательного и вращательного движения  ) вектор углового ускорения сонаправлен с вектором угловой скорости; при замедленном вращении (
) вектор углового ускорения сонаправлен с вектором угловой скорости; при замедленном вращении ( ) вектор углового ускорения направлен противоположно вектору угловой скорости. Направление вектора угловой скорости связано с направлением вращения правилом правого винта. Таким образом, вектор
) вектор углового ускорения направлен противоположно вектору угловой скорости. Направление вектора угловой скорости связано с направлением вращения правилом правого винта. Таким образом, вектор 
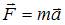 , где
, где  – равнодействующая всех сил, действующих на тело,
– равнодействующая всех сил, действующих на тело,  – его ускорение. Вектор ускорения удобно разложить на две составляющие:
– его ускорение. Вектор ускорения удобно разложить на две составляющие: 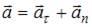 . Тангенциальное ускорение
. Тангенциальное ускорение  направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение
направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение 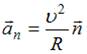 направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории
направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории  0, при движении с постоянной по величине скоростью
0, при движении с постоянной по величине скоростью  0. Следовательно, вектор
0. Следовательно, вектор 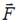 .
. изменился под действием кратковременного удара и стал равным
изменился под действием кратковременного удара и стал равным  , как показано на рисунке:
, как показано на рисунке: 
 . Следовательно, вектор силы направлен так же, как разность импульсов
. Следовательно, вектор силы направлен так же, как разность импульсов 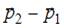 , то есть в направлении 2.
, то есть в направлении 2.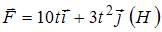 . В момент времени
. В момент времени  проекция импульса (в
проекция импульса (в  ) на ось ОХ равна …
) на ось ОХ равна … . В проекции на ось ОХ
. В проекции на ось ОХ  . Отсюда,
. Отсюда,  следовательно,
следовательно,  .
. движется с коэффициентом трения 0, 5 по наклонной плоскости, расположенной под углом
движется с коэффициентом трения 0, 5 по наклонной плоскости, расположенной под углом 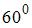 к горизонту. Сила трения (в
к горизонту. Сила трения (в  ) равна …
) равна …
 ,
, 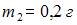 ,
,  . Первая частица находится в точке с координатами (2, 3, 0), вторая – в точке (2, 0, 1), третья – в точке (1, 1, 0) (координаты даны в сантиметрах). Тогда
. Первая частица находится в точке с координатами (2, 3, 0), вторая – в точке (2, 0, 1), третья – в точке (1, 1, 0) (координаты даны в сантиметрах). Тогда  – координата центра масс (в см) – равна …
– координата центра масс (в см) – равна … .Тогда
.Тогда 
 (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 1 c,
(кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 1 c, 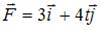 . Модуль силы
. Модуль силы  , и в момент времени t = 1 c
, и в момент времени t = 1 c . Модуль силы (в Н), действующей на точку в момент времени
. Модуль силы (в Н), действующей на точку в момент времени  движется равномерно по вогнутому мосту со скоростью
движется равномерно по вогнутому мосту со скоростью  . В нижней точке сила давления тела на мост вдвое превосходит силу тяжести. Радиус кривизны моста (в
. В нижней точке сила давления тела на мост вдвое превосходит силу тяжести. Радиус кривизны моста (в  ) равен …
) равен … или
или  . Следовательно,
. Следовательно, 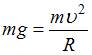 и
и 

 . Для рассматриваемой системы из двух частиц
. Для рассматриваемой системы из двух частиц  . Проекция скорости центра масс на ось ОХ
. Проекция скорости центра масс на ось ОХ 

 и
и  которые движутся так, как показано на рисунке.
которые движутся так, как показано на рисунке.


 то вектор скорости центра масс этой системы ориентирован …
то вектор скорости центра масс этой системы ориентирован … скорость тела изменялась с течением времени, как показано на графике:
скорость тела изменялась с течением времени, как показано на графике: 
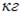 ) равна …
) равна …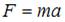 , где а – модуль ускорения, который можно найти из графика зависимости
, где а – модуль ускорения, который можно найти из графика зависимости  :
:  Тогда
Тогда 
 тела от времени t.
тела от времени t. 
 . Изменение скорости
. Изменение скорости  в указанном временном интервале найдено из графика.
в указанном временном интервале найдено из графика. тела от времени t.
тела от времени t. 
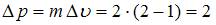 кг·м/с. Изменение скорости
кг·м/с. Изменение скорости  найдено из графика.
найдено из графика.
 , где а – модуль ускорения, который можно найти из графика зависимости
, где а – модуль ускорения, который можно найти из графика зависимости  :
: 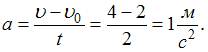 Тогда
Тогда 
 , при этом веревка натягивается силой
, при этом веревка натягивается силой  под углом
под углом  к горизонту. Если коэффициент трения полозьев о поверхность равен
к горизонту. Если коэффициент трения полозьев о поверхность равен 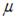 , то уравнение движения санок в проекции на направление движения санок имеет вид …
, то уравнение движения санок в проекции на направление движения санок имеет вид …

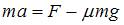

 , где
, где 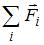 – векторная сумма всех сил, действующих на тело. Для данной задачи это уравнение запишется следующим образом:
– векторная сумма всех сил, действующих на тело. Для данной задачи это уравнение запишется следующим образом: 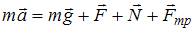 , где
, где  и
и  – сила реакции опоры и сила трения скольжения соответственно. Если ось OX направить по направлению движения, а ось OY – перпендикулярно ему, то уравнение второго закона Ньютона в проекциях на оси выбранной системы координат примет вид:
– сила реакции опоры и сила трения скольжения соответственно. Если ось OX направить по направлению движения, а ось OY – перпендикулярно ему, то уравнение второго закона Ньютона в проекциях на оси выбранной системы координат примет вид:  ,
,  . Выразив из второго уравнения
. Выразив из второго уравнения  и подставив полученное выражение в первое уравнение, получим
и подставив полученное выражение в первое уравнение, получим 
 , где
, где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,  – угловая скорость. По условию диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Тогда
– угловая скорость. По условию диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Тогда  , то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией Е.
, то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией Е. , где
, где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,  , где
, где  – угловое ускорение. Поскольку тормозящий момент не зависит от времени, то и
– угловое ускорение. Поскольку тормозящий момент не зависит от времени, то и  const. Тогда
const. Тогда  , то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией D.
, то есть для момента импульса диска имеет место зависимость от времени, отражаемая линией D. Тема: Динамика вращательного движения
Тема: Динамика вращательного движения  ,
,  ,
,  или
или  ), лежащих в плоскости диска. Не создает вращающего момента относительно рассматриваемой оси сила …
), лежащих в плоскости диска. Не создает вращающего момента относительно рассматриваемой оси сила …

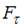 . Тогда момент силы относительно неподвижной оси равен:
. Тогда момент силы относительно неподвижной оси равен:  , где r – радиус-вектор точки приложения силы. В данном случае только для силы
, где r – радиус-вектор точки приложения силы. В данном случае только для силы  . Поэтому
. Поэтому  .
. ,
,  ,
,  и
и  , лежащих в плоскости диска. Если ось вращения проходит через центр О диска и перпендикулярна плоскости рисунка, то длина отрезка a является плечом силы …
, лежащих в плоскости диска. Если ось вращения проходит через центр О диска и перпендикулярна плоскости рисунка, то длина отрезка a является плечом силы …

 . Момент инерции относительно оси, проходяще
. Момент инерции относительно оси, проходяще


