Погрешности косвенных измерений
Задача ставится так: пусть искомая величина z определяется через другие величины a, b, c,..., полученные при прямых измерениях
z = f (a, b, c,...). (1.11)
Необходимо найти среднее значение функции и погрешность ее измерений, т.е. найти доверительный интервал
при надежности a и относительную погрешность Что касается
Абсолютная погрешность косвенных измерений
(кроме случаев, когда показатель равен –1), то сначала удобно вычислить относительную погрешность
а затем абсолютную
Формулы для D z и e z часто приводятся в справочной литературе. Примечания. 1. При косвенных измерениях в расчетные формулы могут входить известные физические константы (ускорение свободного падения g, скорость света в вакууме с и т. д.), числа типа Принято считать, что погрешность округления приближенного числа равна половине единицы того разряда, до которого это число было округлено. Например, p = 3, 14159.... Если взять p = 3, 1, то Dp = 0, 05, если p = 3, 14, то Dp = 0, 005... и т.д. Вопрос о том, до какого разряда округлять приближенное число, решается так: относительная ошибка, вносимая округлением, должна быть того же порядка или на порядок меньше, что и максимальная из относительных ошибок других видов. Таким же образом оценивается абсолютная ошибка табличных данных. Например, в таблице указано r =13, 6 ·103 кг/ м3, следовательно, Dr = 0, 05·103 кг/м3. Ошибки значений универсальных постоянных часто указываются вместе с их средними значениями: с = 2. Иногда при косвенных измерениях условия опыта при повторных наблюдениях не совпадают. В этом случае значение функции z вычисляется для каждого отдельного измерения, а доверительный интервал вычисляется через значения z так же, как при прямых измерениях (все погрешности здесь входят в одну случайную погрешность измерения z). Величины, которые не измеряются, а задаются (если они есть), должны быть указаны при этом с достаточно большой точностью. Например, при определении вязкости жидкости методом Стокса (лабораторная работа № 2) при использовании нескольких шариков разного диаметра абсолютная погрешность будет (см. (1.4))
где i - номер опыта, n - число опытов. В качестве итога всего, сказанного выше, приведем порядок обработки результатов измерений.
|

 (1.12)
(1.12)
 .
. , то оно находится путем подстановки в правую часть (1.11) вместо a, b, c,... их средних значений
, то оно находится путем подстановки в правую часть (1.11) вместо a, b, c,... их средних значений . (1.13)
. (1.13) является функцией абсолютных погрешностей прямых измерений. Если величины a, b, c,... в функцию z = f (a, b, c,...) входят в виде сомножителей в той или иной степени, т. е. если
является функцией абсолютных погрешностей прямых измерений. Если величины a, b, c,... в функцию z = f (a, b, c,...) входят в виде сомножителей в той или иной степени, т. е. если 
 (1.14)
(1.14)
 . (1.16)
. (1.16) дробные множители 1/3, 1/6.... Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность
дробные множители 1/3, 1/6.... Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность  - погрешность округления при вычислениях, которая должна учитываться.
- погрешность округления при вычислениях, которая должна учитываться.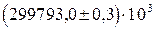 м/c, т.е. D с = 0, 3× 103 м/c.
м/c, т.е. D с = 0, 3× 103 м/c. (1.17)
(1.17)


