Краткие теоретические сведения. При движении жидкости между ее соседними слоями, движущимися с разными скоростями, возникают силы внутреннего трения
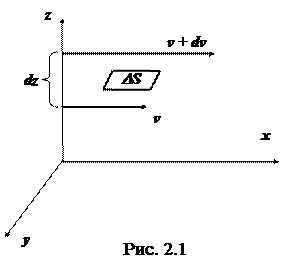
При движении жидкости между ее соседними слоями, движущимися с разными скоростями, возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоев. Возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному слою некоторое количество движения (импульс), вследствие чего он начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, что приводит к торможению быстрого слоя. При переносе импульса от слоя к слою происходит изменение импульса всех слоев. Это значит, что на каждый из слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона). Рассмотрим жидкость, движущуюся в направлении оси х (рис. 2.1). Пусть на расстоянии dz скорости потока отличаются на величину dv. Отношение dv/dz характеризует изменение скорости потока в направлении оси z и называется градиентом скорости. Таким образом, градиент скорости численно равен изменению скорости на единице длины в направлении, перпендикулярном скорости. Согласно закону Ньютона, сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения D S и градиенту скорости:
Величина h (“эта”) называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Если в формуле (2.1) положить численно dv/dz = 1 и D S = 1, то F = h, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся относительно друг друга с градиентом скорости, равным единице. В системе СИ единица измерения [ h ] = кг / (м× с) = Па× с. Коэффициент вязкости h зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Силами внутреннего трения в жидкости обусловлено сопротивление, которое испытывает твердое тело при движении относительно жидкости. Аналитическое решение задачи нахождения силы сопротивления является очень сложным. Подобная задача была решена английским физиком Стоксом лишь для случая очень медленного движения шарика в безграничном объеме жидкости. Сила вязкого трения в этом случае оказалась равной следующей величине:
F = 6 p h r v, (2.2)
здесь r - радиус шарика; v - его скорость относительно части жидкости, находящейся в покое.
|

 (2.1)
(2.1)


