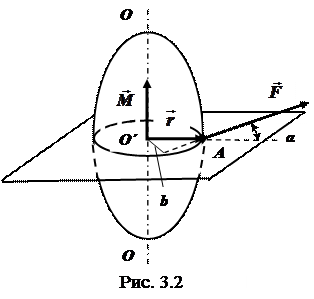
Пусть на тело действует сила 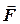 . Примем для простоты, что сила
. Примем для простоты, что сила 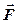 лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2
лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2
А - точка приложения силы 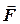 ; О΄ - точка пересечения оси с плоскостью, в которой лежит сила; А относительно точки О΄;
; О΄ - точка пересечения оси с плоскостью, в которой лежит сила; А относительно точки О΄;  - угол между
- угол между 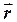 и
и 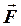 .
.
Моментом силы 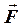 относительно точки О΄ называется вектор
относительно точки О΄ называется вектор 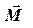 (псевдовектор), определяемый равенством
(псевдовектор), определяемый равенством
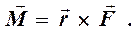 (3.6)
(3.6)
Модуль этого вектора
M = F 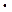 r
r 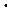 sin a. (3.6, а)
sin a. (3.6, а)
Величина b = r 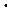 sin a называется плечом силы (кратчайшее расстояние от точки О΄ до линии действия силы).
sin a называется плечом силы (кратчайшее расстояние от точки О΄ до линии действия силы).
Моментом силы относительно оси ОО называется скалярная величина М00, равная проекции на эту ось вектора 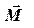 момента силы, определенного относительно точки О΄, лежащей на данной оси.
момента силы, определенного относительно точки О΄, лежащей на данной оси.
В нашем случае
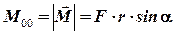 . (3.7)
. (3.7)
В соответствии с выражениями (3.6) и (3.7) вектор  направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).
направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).





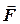 . Примем для простоты, что сила
. Примем для простоты, что сила 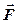 лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2
лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2  - угол между
- угол между 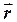 и
и 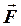 .
.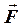 относительно точки О΄ называется вектор
относительно точки О΄ называется вектор 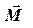 (псевдовектор), определяемый равенством
(псевдовектор), определяемый равенством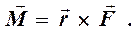 (3.6)
(3.6)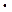 r
r  sin a. (3.6, а)
sin a. (3.6, а)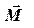 момента силы, определенного относительно точки О΄, лежащей на данной оси.
момента силы, определенного относительно точки О΄, лежащей на данной оси.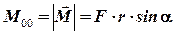 . (3.7)
. (3.7) направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).
направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).


