И метода определения момента инерции
Маятник Обербека представляет собой крестовину, состоящую из втулки 3, четырех спиц 2, укрепленных на одном из концов втулки (рис. 3.4). На спицах размещены грузы 1. Последние могут перемещаться вдоль спиц и закрепляться на них с помощью винтов. Другой конец втулки выполнен в виде шкива 4, на который наматывается нить-шнур. К свободному концу шнура привязан груз 6. Под влиянием этого груза маятник приходит в ускоренное вращательное движение вокруг неподвижной оси. Трение между втулкой маятника и осью практически сведено к нулю установленными на ось подшипниками. Для установки груза 5 на определенной высоте предусмотрен указатель 5. Исходным уравнением для определения момента инерции I маятника является уравнение (3.11), из которого следует, что
где M - вращающий момент, в данном случае - момент силы Т натяжения шнура, приложенной в точке k (рис. 3.4); ε - угловое ускорение маятника.
Нить маятника вертикальна, поэтому угол α в формуле (3.6, а) равен 900, так что
М = T R, (3.13) где R - радиус шкива. Сила T может быть найдена из второго закона Ньютона, записанного для груза 6: ma = mg - T, где m - масса груза, а - ускорение, с которым он опускается, откуда
Т = m (g - а). (3.14)
Таким образом, подставляя (3.14) в (3.13), получим
М = m(g - a) R. (3.15)
Угловое ускорение ε связано с тангенциальным ускорением
В свою очередь,
Ускорение а можно вычислить, если измерить время t опускания груза на определенную высоту h. Действительно,
поэтому
Подставляя (3.17) в (3.16) и (3.15), а затем в (3.12), получим
где d = 2 R - диаметр шкива. Заметим, однако, что второе слагаемое в выражении (3.18) оказывается на практике значительно меньше первого, а потому момент инерции маятника можно вычислить как
Формула (3.19) - рабочая формула для определения I из законов динамики. С другой стороны, как уже отмечалось, момент инерции тела - величина аддитивная. Следовательно, момент инерции маятника Обербека относительно оси вращения можно представить в виде
I = Iв + Iш + 2 Iсп + 4 Iгр (3.20)
где: Iв - момент инерции втулки; Iш - момент инерции шкива; Iпс - момент инерции пары спиц; I гр - момент инерции одного груза 1. Разумеется, все эти моменты инерции в данном случае берутся тоже относительно оси вращения. Так как
Iгр = mгр l12 (груз - материальная точка), где l1 - расстояние от центра масс груза до оси, а mгр - масса груза 1, то
I = (Iв + Iш) + 1/6 × mпс l2 + 4 mгр l12. (3.21)
|

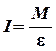 , (3.12)
, (3.12)
 точек на ободе колеса следующим соотношением:
точек на ободе колеса следующим соотношением: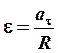 .
. совпадает с ускорением а, с которым опускается груз 6. Следовательно,
совпадает с ускорением а, с которым опускается груз 6. Следовательно,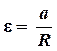 . (3.16)
. (3.16)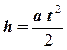 ,
, . (3.17)
. (3.17) , (3.18)
, (3.18)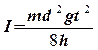 . (3.19)
. (3.19)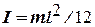 , где l и mпс - общая длина (рис. 3.5) и масса двух спиц, а для случая, когда грузы 1 находятся на концах спиц,
, где l и mпс - общая длина (рис. 3.5) и масса двух спиц, а для случая, когда грузы 1 находятся на концах спиц,



