Открытие и изучение проективной геометрии – прорыв в пространственное сознание, не зависимое от чувственного восприятия
Понятия «проективная геометрия» или «синтетическая геометрия» описывают закономерности, которые не останавливаются на эвклидовой геометрии и перспективе. Они подходят к открытию новых закономерностей в форме закона полярности и описания геометрических бинарных и множественных отношений. Было выяснено, что каждому геометрическому основному элементу (точке, прямой и плоскости) соответствует комплементарный элемент: точке – плоскость, плоскости – точка, а прямой – прямая. То есть прямая комплементарна самой себе. Соответственно, противоположны друг другу, например, такие формы, как плоское точечное поле и пучок плоскостей.[58] Изучение проективной геометрии ведет к преодолению одностороннего, точечно центрированного сознания в пользу динамического представления пространства, которое учитывает контекст, окружение. Можно представить плоскость или прямую как совокупность структурирующих их точек. Тогда они могут рассматриваться как совокупности бесчисленного количества мельчайших кирпичиков, т.е. точек. И наоборот, прямые и точки можно представлять как совокупность всех их структурирующих плоскостей и т.д. Семь основных структур проективного пространства[59]:
Каждая отдельная точка может быть расчленена плоскостями и прямыми, а прямая – плоскостями и точками. Эти три элементарных составляющих геометрии становятся в проективной геометрии полностью равноправными формами зрительного восприятия. К точечному сознанию человека, изучавшего эвклидову геометрию, добавляется сознание прямой и плоскости, благодаря которому процессы, структуры и объекты могут по-новому пониматься в их пространственной структуре. Пространство прекращает быть только «сосудом», в котором находятся и двигаются объекты. Оно приобретает динамическое качество, которое открывается мышлению. Другими словами, пространство прекращает быть сугубо «наглядной формой чувственного восприятия». Оно как идея открывает свои перспективы мышлению. На практике это означает, что каждое образование может быть описано с помощью точек, прямых или плоскостей. Правда, как справедливо заметил Louis Locher-Ernst, современному человеку довольно легко представить прямую в виде совокупности ее точек, и гораздо сложнее – прямую как совокупность ее плоскостей. Поэтому мы приведем здесь еще несколько упражнений:
Рисунок 9: Мы спонтанно переживаем точки как часть чего-то целого, а прямую как носителя этих частей, однако, возможно мыслить точку как целое, а плоскости и прямые какой-либо точки, напротив, признать частями этой точки Обычное, центрированное на самом себе сознание, которое исходит из того, что именно оно является центром происходящего и оттуда рассматривает мир, благодаря этому троякому способу рассмотрения может быть распознано в своей однобокости. Его можно дополнить сознанием прямой и плоскости. Вопрос заключается лишь в том, откуда взять основу для переживания, развивая сознание в направлении точечно–прямо–тоскостного видения пространства. По этому поводу есть замечательное высказывание Louis Locher-Ernst'a: «В последние десятилетия утвердилось мнение, будто задача математики в ее полном объеме состоит в том, чтобы поставлять структурные схемы, придуманные человеческим духом с целью приспособления в чувственном мире. Это знаменует собой шаг вперед по сравнению с господствующим долгое время мнением, высказанным Кантом, о том, что пространство есть застывшая форма зрительного восприятия, которую следует принимать в готовом виде. Еще одним шагом вперед будет познание того, как мышление приходит к созданию совершенно определенных структурных схем для этого. Чтобы понять это, необходимо рассматривать человека в его становлении. В первые годы своей жизни он прорабатывает (без понятийного сознания) вертикаль, в согласованности функций своего правого и левого организма он переживает ширину, а в бинокулярном зрении, а также путем хватания руками, претворяет в жизнь глубину. После того, как формообразующие силы частично освобождаются от своей деятельности на физическом плане, человек оказывается в состоянии создать в мышлении абстрактное пространство в качестве субстрата вышеописанного внутреннего опыта постижения пространства (а не в качестве абстракции чувственного мира). Таким образом, измерения привычного пространства появляются в форме абстрактных отражений ранее осуществлявшейся органической деятельности. Если удастся, возможно – без непосредственного осознания этого, создать в мышлении отражения еще более ранних видов деятельности (осуществлявшихся в период, начинающийся за несколько лет до рождения, когда индивидуальность, спускаясь на землю, обволакивается формирующими силами из мирового окружения), то возникает совершенно другое понятие пространства, а именно понятие противопространства.[60] Однако, следует помнить о том, что закон противоположности точки и плоскости с посредничающими между ними прямыми получен не путем эксперимента и не с помощью доказательства, но является феноменом как таковым, т.е. носит характер аксиомы. Нижеследующие рисунки иллюстрируют эту феноменологическую закономерность. В рис. 10а и 10b речь идет о поляризации куба, при этом появляется октаэдр. Каждый из вас может легко сконструировать подобный октаэдр внутри уже нарисованного куба, следуя закону противоположности. Для этого следует в центре каждого квадрата, ограничивающего соответствующую плоскость куба, поставить точку. А на месте восьми вершин куба, где пересекаются три ребра, опять-таки по закону противоположности возникают плоскости, ограниченные тремя прямыми. Эти восемь плоскостей возникающего таким образом октаэдра получаются путем соединения середин квадратов шести поверхностей куба. Очевидно, что эти два противоположных тела являются представителями пяти платоновых тел. Эти пять платоновых тел выделяются среди других геометрических тел тем, что они обладают совершенно регулярным членением их вершин и плоскостей. Подобно кубу и октаэдру, также полярны друг другу пентагон–додекаэдр (он состоит из двенадцати правильных пятиугольников) и икосаэдр (он состоит из двадцати правильных треугольников). Пятое из Платоновых тело, тетраэдр, является противоположным самому себе.
Рисунок 10: Гексаэдр и октаэдр, будучи абсолютно правильными телами, полярны друг другу Изображенные ниже тела, кубооктаэдр и ромбододекаэдр, не относятся к Платоновым телам, однако они противоположны друг другу.
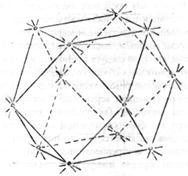
Рисунок 11: Кубооктаэдр и ромбододекаэдр, являясь полу–правильными (не Платоновыми телами), полярны друг другу
|