Арифметическое представление пространства и времени

При абстрактном рассмотрении про­странство и время представляются вначале просто как измеряемые величины. Потреб­ность в измерении появляется даже раньше, чем происходит оформление математики как теоретической науки, например при землемерных работах или в астрономии, где необходимо считать дни и годы. Но любой измеримый объект, вообще говоря, характеризуется своей мерностью, то есть количеством мер, которыми необходимо оперировать, чтобы определить его вели­чину. Например, линия, характеризуемая только своей длиной, является одномерной, тогда как поверхность уже двухмерна (дли­на и ширина), а пространство — трехмерно (высота или глубина, длина и ширина). Кроме того, отмеривание предполагает, что для каждого из трех измерений опреде­ляют точку отсчета и единицу измерения, которую откладывают, начиная с исходной точки, столько раз, сколько необходимо, чтобы полностью покрыть измеряемую ве­личину. Так, и время оказывается измери­мым, поскольку можно определить основ­ную единицу времени, например продолжи­тельность дня или секунды, и можно отсчитать эту основную единицу столько раз, сколько необходимо, начиная с данной

 

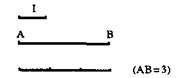
точки отсчета. Таким образом, время пред­ставляет собой одномерную сущность в том же смысле, что и линия, которая по этой причине может его символизировать. Поскольку пространство и время — изме­ряемые величины, их можно определить ко­личественно, используя для этого меру. На этом уровне абстрагирования пространство и время не отличаются от чисел и, похоже, могут являться объектом изучения науки о числах или арифметики.

а) Пифагорова арифметика

Пифагорейцы попытались дать чисто арифметическое определение пространства, отождествив точку в пространстве с ариф­метической единицей. Такое отождествле­ние оправданно при решении задач, связан­ных с точным измерением величин. Пред­положим, что у нас есть измеряемая величина (например, отрезок AB), тогда, конечно, может случиться так, что единица измерения будет точно укладываться (один или несколько раз) в измеряемой величине:

Но такая возможность является исключе­нием. Если измеряемая величина содержит по отношению к точно откладываемой еди­нице измерения избыток или недостаток, необходимо будет для измерения этого из­бытка или недостатка взять дробную часть этой единицы измерения:

Если хотят добиться точного значения, до­статочно взять более мелкую единицу из­мерения: например, отрезок в 2, 5 см содер­жит ровно 25 мм. Следовательно, чтобы иметь возможность измерить любое про-

странство, достаточно взять за единицу из­мерения наименьшую возможную часть пространства, то есть точку.

Любая геометрическая операция, сводя­щаяся к измерению величины, может, сле­довательно, найти свое точное соответ-ствие в арифметическом действии. В одно­мерном случае измерение, состоящее в откладывании единицы, начиная от точки отсчета, является сложением:

Измерение поверхности предполагает, что, определив ее длину, определяют также ее ширину — размерность, перпендикулярную длине. Следовательно, надо произвести два измерения в виде двух перпендикулярных линий. По-латыни говорят: " Ducere lineam in lineam", и эта операция есть productio, или произведение результата, то есть ум­ножение:

Наиболее характерной формой умножения является возведение в квадрат (1 χ 1 = l²); оно позволяет определить единицу площади I², или квадрат со стороной 1. Умножив на дополнительное измерение, можно опреде­лить единицу объема I³, или куб с ребром 1. При таком подходе видно, что существу­ет полное соответствие между арифмети­ческими и геометрическими операциями. Это также означает, что арифметические операции должны быть выражены через их геометрическое представление. При этом, если количественную величину рассматри­вать только как число, может показаться, что умножение не отличается от сложения. Рассуждая таким образом, умножение 2 на 3 можно отождествить со сложением три раза по два:

2x3 = 6

2 + 2 + 2 = 6.

 

Но с точки зрения пифагорейской арифме­тики сложение, которое сохраняет ту же размерность, качественно отличается от умножения, которое производит дополни­тельную размерность:

Отличие особенно ощутимо в случае опера­ций только с единицей, поскольку ее при­бавление к самой себе порождает ряд целых чисел, в то время как ее умножение на саму себя создает ряд единиц меры в последова­тельных измерениях:

1 + 1 = 2; 1 + 1 + 1 = 3,... 1 χ 1 = \²; 1 χ 1 χ 1 = I³.

Впрочем, в этом случае сама арифметичес­кая формула показывает, что умножение не сводится к повторению операций сложения. Следовательно, полное соответствие арифметических и геометрических опера­ций позволяет изобразить геометрически характерные свойства числа. Например, ре­зультат умножения целого числа на само себя может быть представлен в виде квад­рата, тогда как умножение двух различных целых чисел дает прямоугольник:

Представляется оправданной и обратная операция, с помощью которой характерные геометрические фигуры (линия, квадрат, прямоугольник, треугольник и т. д.) можно представить арифметически, используя точ­ки, из которых они состоят.

Тем не менее данное предположение оказалось ложным. В самом деле, если до­пустить, что линии состоят из точек, тогда необходимо, чтобы данный отрезок прямой

линии всегда можно было выразить опре­деленным числом точек. Таким образом, необходимо, чтобы отношение длин двух отрезков всегда можно было выразить арифметически в виде отношения целых чи­сел. Однако сам Пифагор доказал, что ес­ли, предположив такую возможность, по­пытаться выразить соотношение между длиной стороны квадрата и длиной его диагонали, то получаются противоречивые следствия:

Возьмем квадрат со стороной а и диагона­лью d. Предположим, что отношение а к d можно записать как отношение меж­ду целыми числами, то есть в виде дроби (μ ί α). Приведем это соотношение к прос­тейшему выражению таким образом, что­бы а и d были взаимно простыми числами, то есть не имели никакого другого общего делителя, кроме единицы.

Теорема Пифагора дает простое соотно­шение между and. Действительно, в равнобедренном прямоугольном треу­гольнике АСВ квадрат, построенный на гипотенузе d, равен сумме квадратов, по­строенных на сторонах прямого угла, где каждая сторона равна а:

(P = 2d^! (Е).

Таким образом, d² равно целому числу, умноженному на 2, то есть четному числу, а поскольку корни четного квадрата числа четные, то и d является четным числом. Так как а и d являются взаимно простыми числами, они не могут иметь общий дели­тель, равный 2, и если d — четное число, то α — нечетное. Но если d является чет­ным числом, его можно разделить на 2. Значит:

Уравнение (Е) может, таким образом, быть представлено как:

(2с)² = 2^ или 4с² = 2α ² или 2с² = а*.

 

Таким образом, а² равно четному числу, и поскольку корни четного квадрата явля­ются четными числами, то а само являет­ся четным*.

Таким образом, если длину стороны квад­рата выразить определенным числом то­чек, то невозможно длину его диагонали выразить также определенным числом. Следовательно, они не имеют наименьшей общей меры, то есть эти длины несоиз­меримы. Этот результат тем более впечат­ляющий, что между площадями квадратов, возведенных на этих двух линиях, сущест­вует очень простое соотношение — Ч г, поскольку квадрат, построенный на диаго­нали данного квадрата, имеет площадь вдвое большую, чем площадь данного квадрата.

Если взять квадрат со стороной 1, то его диагональ будет являться стороной квад­рата, площадью равной 2, или, другими словами, ее длина будет равняться " корню из 2", поскольку на пифагорейском языке термин " корень" обозначает линию, на которой возводят квадрат. Нет ничего про­ще, чем геометрическое построение тогда как арифметически определенным числом эту величину выразить невозмож­но. В результате после провала пифагорей­ской программы греки перешли исключи­тельно к геометрической ориентации своей математики, при которой сами арифме­тические операции изображаются геомет­рически.

Однако геометрическое изображение
приводит к парадоксальным выводам.
Нет ничего проще, построив отрезок такой
длины геометрически, отложить его цир­
кулем на линии, разделенной на единицы
(где единица — катет треугольника). По­
скольку отрезок больше единицы
и меньше двух, можно попытаться найти,
разбивая единицу на части, меру длины,
позволяющую его измерить. Но поскольку
доказано, что 1 и несоизмеримы, сле­
дует признать, что, как бы мелко мы ни
дробили единицу, мы никогда не достиг­
нем

¹ См.: Евклид. Начала. Кн. X. Приложение 27. Использованное рассуждение было подтвер­ждено Аристотелем в " Первой аналитике". Гл. 23, 41 а 26—27 (Аристотель. Соч.: В 4 т. М., 1978. Т. 2. С. 168).

Тем не менее такое дробление можно осуществлять столько раз, сколько сущест­вует целых чисел, то есть бесконечное число раз (хотя на рисунке указаны лишь несколь­ко делений на два, соответствующих после­довательным степеням двойки). Каждое из этих делений соответствует локализации точки на отрезке между 1 и 2, но бесконеч­ное число этих точек не исчерпывает число точек отрезка, потому что ни одна из них не соответствует той, на которой кончается длина

Этот парадокс объясняет, почему пифа­горейцы выбрали термин " иррациональ­ный" для обозначения На древнем мате­матическом языке " рацио" (" raison" — ра­зум) обозначает определенное соотношение между двумя членами. В математическом смысле число является иррациональным просто потому, что оно не находится в стро­го определенном соотношении со стороной квадрата. Но выбор термина " иррациональ­ный" для обозначения того, что, по сути, есть лишь простая несоизмеримость, пока­зывает, что пифагорейцы ощутили неудачу своего учения как потрясение основ разум­ности. Однако это потрясение, начавшееся внутри базисных положений пифагорейской школы, привело к следствиям, выходящим за пределы их теории. Действительно, дока­зательство того, что операция деления дан­ной линии пополам, сколько бы ее ни повто­рять, никогда не сможет исчерпать совокуп­ность всех точек, составляющих эту линию, привело к появлению аргументов, которые Зенон направил против пифагореизма.

Ь) Аргументы Зенона

Согласно свидетельству Платона рас­суждения Зенона из Элей направлены на то, чтобы поддержать тезис Парменида о

 

единстве и непрерывности бытия и опроверг­нуть пифагорейский тезис множественности:

В действительности это сочинение поддер­живает рассуждение Парменида против тех, кто пытается высмеять его, утверж­дая, что если существует единое, то из этого утверждения следует множество смешных и противоречащих ему выводов. Итак, мое сочинение направлено против допускающих многое, возвращает им с из­бытком их нападки и старается показать, что при обстоятельном рассмотрении их положение " существует многое" влечет за собой еще более смешные последствия, чем признание существования единого'.

Учение Парменида о едином бытии, по су­ществу, является антитезой пифагорейского учения. Пифагорейское учение предполагает множественность и дискретность, посколь­ку в последовательности чисел имеет место резкий скачок от одной единицы к другой и в то же время между точками, которые геометрически изображают числа, сущест­вует пустое пространство. Напротив, бытие Парменида, как и геометрическое простран­ство, " одно непрерывное" ². Несомненно, что тезис Парменида имеет парадоксальные и противоречивые следствия³. Но можно надеяться придать ему некоторую обосно­ванность, показывая, что противополож­ный тезис приводит к следствиям еще более смехотворным и противоречивым. Именно этой задаче посвятил себя Зенон со всей диалектической виртуозностью, от которой у нас, к сожалению, сохранились лишь неко­торые результаты.

Первый аспект его аргументации на­правлен прежде всего против пифагорей­ского тезиса, согласно которому " многое состоит из сложения единиц'" ¹. Действи­тельно, для того чтобы единица производи­ла многое путем последовательных сложе­ний, нужно, чтобы сложение или вычитание единицы могло сделать большим или мень­шим количество, к которому ее прибавля­ют или из которого вычитают. Однако пи­фагорейцы сами отождествляют единицу

'Платон. Парменид. 128 cd // Соч.: В 4 т. М., 1993. Т. 2. С. 348.

² Парменид. В. 8 6 (ДК) // Фрагменты ранних греческих философов. Ч. 1. М., 1989. С. 290.

³Ср. наст. изд. Гл. 6. С. 189—190.

⁴ Зенон в изложении Филопона: Philopon. Commentaire ä Aristote, Physique. Ed. Acad. Berol. P. 42 (29 A 21 DK).

с точкой, которая не может увеличивать то, к чему ее прибавляют. В самом деле, " плос­кость и линия, если их прибавлять, в одном случае увеличивают, а в другом нет..." ⁵. Они способны увеличивать то, к чему их прибав­ляют, если это сложение происходит в соот­ветствии с их собственной размерностью. Например, линия, обладающая длиной без толщины, может добавлять свою длину к уже существующей длине, но она не может образовать площадь, добавляя к другой ли­нии толщину, которой она не обладает:

Аналогично нельзя добавлять площади к площадям, чтобы получить объемы. Но если линии и площади могут добавляться друг к другу в том смысле, в котором они являются одно- или двухмерными, то точка — это то, что не имеет размерности. Таким образом, если единица точечная, ее нельзя прибавить к самой себе, чтобы составить множество: прибавление точки к самой себе " совершенно не" ⁶ увеличит ее и никогда нельзя будет выйти за пределы единицы, чтобы образовать множественность.

Эта неспособность точки выйти за свои пределы проиллюстрирована хорошо из­вестными аргументами (апориями), с помо­щью которых Зенон показывает невозмож­ность объяснить движение с точки зрения пифагорейских тезисов. Первый из его ар­гументов — это апория " Дихотомия", или бесконечное деление траектории пополам:

...О несуществовании движения на том ос­новании, что перемещающееся [тело] должно дойти до половины прежде, чем до конца⁷.

Чтобы добраться из А в В, действительно, нужно сначала достичь С — середины AB, но, чтобы добраться от А до С, нужно сначала достичь D — середины АС, E — се­редины AD, и так до бесконечности:

⁵ Зенон в изложении Аристотеля см.: Ари­стотель. Метафизика. III 4, 1001 b 11—13 // Соч.: В 4 т. М., 1975. Т. 1. С. 114.

'Там же. 13.

''Аристотель. Физика. VI 9, 239 b 11—13 // Соч. М., 1981. Т. 3. С. 199.

 

Таким образом, никогда не удастся выйти из А, чтобы достичь В, поскольку для этого необходимо преодолеть беско­нечность точек одна за другой, что невоз­можно за " конечное время" '.

Второй аргумент — это апория, кото­рую называют " Ахилл" ², потому что она показывает, что, как бы быстро ни бежал Ахилл, он никогда не сможет настичь чере­паху, если на старте она была на какое-то расстояние впереди него:

Самое медленное [существо] никогда не сможет быть настигнуто в беге самым быстрым, ибо преследующему необходи­мо прежде прийти в место, откуда уже двинулось убегающее, так что более мед­ленное всегда должно будет на какое-то [расстояние] опережать [преследующего]³.

Действительно, когда Ахилл достигнет точ­ки Р, откуда стартовала черепаха, послед­няя продвинется до точки Pi, но, когда он будет в Pi, она будет в Р₂, и так до бес­конечности:

случае необходимо признать, что в данное мгновение стрела занимает длину (напри­мер, CD), где она " находится в равном [себе месте]" ⁶, то есть занимает длину, рав­ную самой себе. Однако необходимо при­знать, что " всегда... всякое [тело] покоит­ся" ⁷ или перемещается, потому что покой и движение противоположны и ничего тре­тьего быть не может. Однако находиться в состоянии покоя означает быть в про­странстве, точно равном самому себе. В данное мгновение стрела, таким образом, неподвижна в CD:

Быть в движении означало бы для нее не совпадать с CD, а перейти за пределы D. Таким образом, если допустить, что " пере­мещающееся [тело] в момент " теперь" все­гда [находится в равном себе месте]" ⁸, то необходимо также допустить, что движение — это последовательность неподвижных состояний.

" И это рассуждение основывается на делении пополам", то есть в том, что касается ее принципа, эта апория такая же, как апория " Дихотомии"; " отличается же [от предыдущего] тем, что взятая величина делится не на две равные части" ⁴. Дейст­вительно, начальную стартовую разницу АР делят не на две равные части, а в соот­ветствии с числом, которое выражает со­отношение между скоростью Ахилла и скоростью черепахи; при этом показыва­ется, что, как бы мала ни была эта разница, всегда можно найти еще мень­шую величину, и она никогда не будет нулевой.

" Третье, о котором только что было упомянуто, состоит в том, что летящая стрела стоит неподвижно; оно вытекает из предположения, что время слагается из [от­дельных] " теперь" ⁵. Действительно, в этом

¹ Аристотель. Физика. VI 2, 233 а 22—23 // Соч. Т. 3. С. 183.

² См. там же. 9, 239 b 14. С. 199.

'Там же. 15—18.

" Там же. 18—20.

⁵ Там же. 30—32. С. 200.

с) Содержание континуума

Внутренние трудности пифагорейского учения и успех аргументации элеатов окон­чательно убедили греческих математиков встать на позиции геометрии — науки о не­прерывном пространстве. Однако, как бы ни была теоретически интересна греческая математика, особенно модель всякой тео­ретической науки, содержащаяся в " Нача­лах" Евклида, исключительно геометричес-кая ориентация математики имеет все же тот недостаток, что величина континуума не поддается вычислению. Правда, проце­дуры геометрического построения позволя­ют определить простым и точным спосо­бом величины, которые арифметика не мо­жет определить точно, например иррациональную величину Но геомет­рическое построение с помощью линейки и циркуля гораздо беднее возможными

«Там же. 6. С. 199. 'Там же. 5—6. " Там же. 6—7.

 

комбинациями по сравнению с операци­ями вычисления. С появлением современ­ной науки сведение математики к геомет­рии стало все больше рассматриваться как препятствие на пути развития знания. Именно это препятствие математики, на­чиная, в частности, с Кеплера, пытались обойти, выдвигая процедуры вычисления континуума, то есть процедуры, позволя­ющие при рассмотрении величины кон­тинуума применить арифметические опе­рации.

Одним из первых примеров таких процедур является доказательство Кеп­лером положения (уже найденного Архи­медом геометрически) о равенстве площа­ди круга половине произведения радиуса на длину окружности. Кеплер полагает, что площадь круга образуется путем сложения одних радиусов с другими.

Для этого надо предположить, что каждый радиус имеет площадь, которую можно отождествить с площадью бесконечно уз­кого треугольника с высотой, равной ради­усу, и основанием, равным длине точки на окружности. Площадь такого треугольни­ка равна половине произведения высоты (R) на основание (равное точке, то есть нулю):

Если обозначить количество точек окруж­ности через С, то будет видно, что в круге столько же радиусов, сколько и таких то-

чек, или что площадь круга равна произ­ведению площади каждого радиуса на С:

Таким было положение, которое необходи­мо было доказать. В своей " Геометрии не­делимых" Кавальери систематически ис­пользовал подобные процедуры. Таким об­разом, он заново доказывал теоремы Евклидовой геометрии, рассматривая ли­нии как состоящие из точек, площади — как состоящие из линий, а объемы — как состоящие из площадей. Например, Евклид доказал, что площадь треугольника равна половине произведения его основания на высоту. Чтобы арифметически интерпре­тировать это положение, можно рассмат­ривать треугольник как образованный множеством параллельных линий, заполня­ющих его площадь от вершины до основа-

ния. Эти линии могут быть определены количеством содержащихся в них точек (на­пример, число Ъ определяет величину ос­нования), а число этих линий — количест­вом (h) точек, находящихся на их пересече­нии с высотой. Таким образом, получается ряд h чисел, регулярно возрастающих от вершины (равной точке, то есть равной ну­лю) до основания (равного Ь). А согласно простому правилу исчисления рядов сумма их членов равна половине произведения суммы крайних членов на количество чле­нов. Например:

Если применить это правило к арифмети­чески определенному треугольнику, то мы получим формулу, ранее доказанную Евк­лидом:

 

_ς _ (нуль + b)h _ b χ h
*~ 2 - 2

Таким же способом заново доказывается теорема о том, что площадь трапеции рав­на половине произведения суммы основа­ний на высоту. Следует отметить, что при таком подходе геометрические фигуры сно­ва выглядят как если бы они были состав­лены из чисел, расположенных в виде тре­угольника или трапеции:

Таким образом, геометрия неделимых снова пускает в ход пифагорейскую интер­претацию.

Однако " обоснования" этих методов " зиждутся" исключительно " на правильнос­ти результатов", на " правильности, дока­занной из других оснований" ¹. Но у методи­ки, которая приводит к результату, недо­стает ясности, и она может даже рассматриваться как некорректно обосно­ванная. Например, методика Кеплера сос­тоит в умножении определенного количест­ва (длины радиуса) на бесконечно малое количество (точку окружности).

Однако, в соответствии с обычными арифметическими правилами, необходимо было бы либо рассматривать бесконечно малое количество как нуль (и в этом случае его произведение на R было бы равно ну­лю), либо рассматривать это количество как какую-то определенную величину (и в этом случае ее произведение на R не было бы равно R). Тем не менее " нельзя обойтись без представления", что бесконечно малые " не равны нулю, но они столь незначитель­ны, что их можно оставить без внимания" ². Что касается метода Кавальери, то он так-

же неправилен — в том смысле, что парал­лельные линии, составляющие площадь треугольника или трапеции, рассматрива­ются как члены арифметической прогрес­сии, хотя нет возможности определить, на­сколько один член прогрессии отличается от другого (и просто предполагается, что это отличие равняется одной и той же вели­чине). Наиболее же парадоксальным явля­ется то, что, несмотря на приближенный характер и даже противоречивость мето­дов, " получается результат, который не только довольно точен и столь близок [к истинному результату], что можно не об­ращать внимания на разницу, но и совер­шенно точен" ³. Таким образом, исчисление континуума лишь по видимости преодоле­вает противоречие континуума и дисконти­нуума: в действительности же противоре­чие не только не преодолевается, но фак­тически оказывается введенным в саму структуру операционных методов.