III. Моделирование связи социально-экономических явленийОтбор факторных признаков, влияющих на уровень балансовой прибыли, был осуществлен на основе логики экономического анализа, а также реализации корреляционного анализа. Были построены и проанализированы матрицы парных и частных коэффициентов корреляции. Матрица парных коэффициентов корреляции.
Значение парных коэффициентов корреляции свидетельствует о сильной связи ( Значимость парных коэффициентов корреляции проверим на основе t-критерия Стьюдента. Матрица расчетных значений t-критерия Стьюдента.
Все расчетные значения t-критерия больше tkp = 1, 682 (α = = 0, 05; v = 48 – 2 = 46), что свидетельствует о значимости коэффициентов корреляции. Таким образом, в модель могут быть включены все факторные признаки, перечисленные в табл. 13.1. Построение модели балансовой прибыли банков РФ было осуществлено методом пошагового регрессионного анализа на основе последовательного исключения факторов (табл. 13.4). Таблица 13.4 Модели пошагового регрессионного анализа балансовой прибыли и характеристики их точности
На втором шаге было получено значимое уравнение регрессии (Fp> Fkp), содержащее значимые параметры ( Анализируя параметры модели регрессии, можно сделать следующие выводы: - на каждую 1 тыс. руб. собственного капитала коммерческих банков на 01.01.97 г. приходилось 0, 2 тыс. руб. прибыли; - кредитная политика банков позволила получать 0, 08 тыс. руб. с 1 тыс. руб. выданных ссуд; - каждая 1 тыс. руб. вложений в ценные бумаги дает отдачу в размере 0, 03 тыс. руб. прибыли. Для более полной интерпретации модели балансовой прибыли рассчитаем коэффициенты эластичности (ЭХi) и коэффициенты регрессии в стандартизованном масштабе (β Xi) и (Δ Xi) – коэффициенты. Результаты сведены в табл. 13.5. Таблица 13.5 Оценки коэффициентов модели балансовой прибыли
Анализ коэффициентов эластичности показывает, что при увеличении собственного капитала на 1% прибыль увеличивается на 0, 5%, а объем вложений в ценные бумаги – только на 0, 01%. Расчет β Xi позволил отойти от размерности признаков (что не присуще параметрам aXi) и определить приоритетность влияния факторов на балансовую прибыль. Совокупный взаимосвязанный анализ представленных в табл. 13.5 коэффициентов позволил проранжировать факторы по уровню их значимости на величину балансовой прибыли, которая в первую очередь определяется величиной собственного капитала. Расчет частного коэффициента детерминации для фактора х1 подтверждает этот вывод:
31% изменения балансовой прибыли обусловлен вариацией величины собственного капитала. Если учесть, что множественный коэффициент детерминации составил 92, 9%, то изменение собственного капитала на 1/3 определяет уровень доходов банков Деятельность коммерческих банков на рынке ценных бумаг на 18, 6% ( Таким образом, в ходе анализа были выявлены и оценены направления, определяющие доходность крупнейших коммерческих банков: кредитная политика и активная работа на рынке ценных бумаг. Пример. Проанализируем динамику, тенденции изменения и определим перспективную численность официально зарегистрированных в службе занятости безработных (тыс. чел.). Сначала рассчитаем аналитические показатели динамики (Δ i, ТP и ТПР), (табл. 13.6) и средние ( Анализ Δ i, ТP и ТПР показал несомненный рост численности безработных за весь рассматриваемый период времени с I квартала 1992 г. по IV квартал 1995 г. Исключение составляет III квартал 1993 г., когда численность безработных по сравнению с предыдущим кварталом снизилась на 24 тыс. человек (Δ ц = 712, 0 – 736, 0 = -24) и при этом составила 96, 7% ( уровня II квартала. Снижение числа безработных произошло на 3, 3% (ТПРц = 100% – 96, 7% = 3, 3%). Однако по сравнению с I кварталом 1992 г. происходит постоянный рост данного показателя. С целью получения обобщающей характеристики ряда динамики были определены средние показатели:
Таблица 13.6 Аналитические показатели динамики численности официально зарегистрированных в службе занятости безработных
Средний абсолютный прирост
Это означает, что в среднем за рассматриваемый период число безработных увеличивалось на 142, 56 тыс. человек. Средний темп роста Средний темп прироста: В среднем за рассматриваемый период численность безработных возрастала на 23, 5%. Важной задачей статистики при анализе рядов динамики и основной предпосылкой при прогнозировании на их основе является выявление наличия, характера и направления тенденции развития изучаемого социально-экономического явления или процесса. В рядах динамики можно наблюдать тенденции трех видов: среднего уровня, дисперсии, автокорреляции. Последняя, как правило, характерна для связных рядов динамики. В статистике разработан ряд методов выявления перечисленных видов тенденции. На практике наиболее широкое распространение получили методы Фостера и Стюарта и сравнения средних уровней ряда динамики. По данным табл. 13.6 определим наличие основной тенденции методом сравнения средних уровней ряда. Разделим ряд на две части: n1 = 8, n2 = 8. По каждой вычислим средние и дисперсии:
Проверим гипотезу о равенстве дисперсий при уровне значимости α = 0, 05: Fkp (α = 0, 05; v1 = n2 – 1 = 7; v2 = n1 – 1 = 7) = 3, 8. Так как FP < Fkp, то нулевая гипотеза о равенстве дисперсий совокупностей ( Проверка основной гипотезы о равенстве средних уровней двух нормально распределенных совокупностей n1 и n2 осуществляется на основе t-критерия Стьюдента:
tkp (α = 0, 05; v = n – 2 = 16 – 2 = 14) = 2, 121. Так как |tp| > tkp, то нулевая гипотеза о равенстве средних отвергается, расхождение между вычисленными средними существенно, следовательно, существует тенденция средней. Результаты расчетов на основе метода Фостера-Стюарта представлены в табл. 13.7. Таблица 13.7 Расчетная таблица для определения характеристик метода Фостера-Стюарта
S = Σ St = 14, где St = Ut + 1t d = Σ dt = 14, где dt = Ut – 1t. С помощью величины S проверяется гипотеза о наличии тенденции в дисперсиях: где σ 1 – средняя квадратическая ошибка S; σ 2 – средняя квадратическая ошибка d; μ – математическое ожидание S. σ 1, σ 2, μ – табличные значения. Проверка осуществляется на основе t-критерия Стьюдента:
tkp (α = 0, 05; v = n – 1 = 15) = 2, 131. Так как tP1 > tkp и tP2 > tkp гипотезы об отсутствии тенденции средней и дисперсии отвергаются, т.е. в ряду динамики существует тенденция и средней, и дисперсии, а следовательно, существует и тренд. Проанализировав наличие тенденции двумя методами, видно, что существует некоторое противоречие в результатах: в первом методе – отсутствует тенденция дисперсии, во втором – нет. Решение данного вопроса может быть найдено в повторной проверке результатов методами выявления тенденции не по ее видам, а в целом в ряду динамики. С этой целью можно использовать фазочастотный критерий знаков разностей Валлиса и Мура. Нулевая гипотеза (Н0) заключается в утверждении, что знаки последовательных разностей (Уi+1 – Уi) (знаки абсолютных цепных приростов) образуют случайную последовательность. Последовательность одинаковых знаков называется фазой. Расчетное значение фазочастотного критерия разностей определяется по формуле
где h – число фаз; n – число уровней.
Таблица 13.8 Расчетная таблица для определения скользящей средней
Так как tp = 4, 29 > tkp = 1, 87 (по таблице значений вероятности tkp для фазочастотного критерия), то нулевая гипотеза отвергается, уровни ряда численности официально зарегистрированных безработных не образуют случайную последовательность, следовательно, имеют тенденцию. После того как выявлено наличие тенденции по видам, необходимо определить основную тенденцию развития и ее направление. Это можно осуществить на основе метода скользящей средней и аналитического выравнивания. Сглаживание ряда динамики числа безработных осуществлено на основе четночленной и нечетночленной скользящей средней. Анализ данных табл. 13.8 подтвердил наличие возрастающей тенденции в ряду динамики числа безработных РФ. Более эффективным способом определения основной тенденции является аналитическое выравнивание. Рассмотрим применение метода аналитического выравнивания по прямой как наиболее простой функции времени Анализ аналитических показателей динамики численности официально зарегистрированных в службе занятости безработных (табл. 13.9) показывает целесообразность использования параболы для описания тенденции.
а0 = 1103; а1 = 72, 3; а2 = 0, 9. Отсюда: Средняя квадратическая ошибка
Таблица 13.9 Расчетная таблица для определения параметров модели параболы второго порядка численности официально зарегистрированных безработных
Средняя ошибка аппроксимации
После того как выявлена тенденция и определено ее направление, можно приступать к прогнозированию численности официально зарегистрированных безработных. В прогностике разработано свыше 130 методов прогнозирования. Рассмотрим простейшие из них, к которым относятся методы прогнозирования на основе: 1) среднего уровня ряда; 2) среднего абсолютного прироста; 3) среднего темпа роста. Поданным нашего примера первым методом прогнозировать нельзя, так как он применим к стационарным рядам динамики, а у нас имеет место ярко выраженная тенденция. Прогнозирование методом среднего абсолютного прироста возможно при выполнении условия:
Расчет характеристик представлен в табл. 13.10.
Таблица 13.10 Расчетная таблица
Так как Методом среднего темпа роста модель прогноза имеет вид:
где L – период упреждения.
Прогнозное число безработных на: I квартал 1996 г. составит II квартал 1996 г.:
Средняя квадратическая ошибка
Прогнозная численность официально зарегистрированных в службе занятости безработных, полученная на основе экстраполяции параболы второго порядка, составила на I квартал 1996 г.:
II квартал 1996 г.:
Сравнив модели прогноза методом экстраполяции параболы второго порядка и методом среднего темпа роста на основе средней квадратической ошибки, видно, что наиболее точным является прогноз численности официально зарегистрированных в службе занятости безработных методом экстраполяции на основе параболы второго порядка. Прогноз методом среднего темпа роста σ ОШ = 430, 2, а методом экстраполяции параболы σ ОШ = 75, 6 (75, 6 < 430, 2). Таким образом, изучение социально-экономических явлений и процессов на основе комплексной методики анализа, обобщения и прогнозирования на базе широкого применения традиционных статистических и математико-статистических методов позволит наиболее глубоко и досконально исследовать причинно-следственные связи и закономерности и показать природу изучаемого явления или процесса.
|
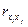> 0, 7) между всеми признаками и влиянием их на результативный – балансовую прибыль.
= 43264, 99 +0, 13x1 +0, 07x2+
0, 02х3+
0, 0 1х4
). Этот вывод подтверждается и анализом средней ошибки аппроксимации (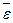
= 1, 99% < 12%).
.
) определяет прибыльность банков.
) показатели.
)
.
– средняя численность официально зарегистрированных в службе занятости безработных за период с I квартала 1992 г. по IV квартал 1995 г.
.
.
.
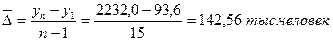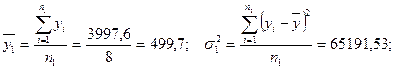
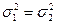) не отвергается, дисперсии различаются незначимо, расхождение между ними носит случайный характер.
;
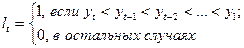
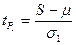, а на основе величины d-тенденции в средней: 
,
;
;
,
.
= f(t). На практике же целесообразно выбор функции осуществлять либо на основе анализа аналитических показателей ряда динамики, либо методом перебора ряда функций и выбора той, которой соответствует наименьшая средняя квадратическая ошибка и средняя ошибка аппроксимации.
.
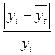
, что свидетельствует о достаточной значимости (адекватности) функции.
.
;
;
.
≤ ρ 2 (17851, 82 > 12129, 58), то прогнозировать численность безработных на основе ряда динамики с I квартала 1992 г. по IV квартал 1995 г. методом среднего абсолютного прироста нельзя.
,
.
= 2232 · 1, 2351 = 2756, 52 тыс.человек;
= 2232 · 1, 2352 = 3404, 3 тыс. человек, или
=2756, 52 ·1, 235 = 3404, 3 тыс. человек.
.
= 1003 + 72, 3 ·17 + 0, 9 · 172 = 2492, 2 тыс. человек;
