Методические указания и решение типовых задач. Экономический индекс– это относительная величина, которая характеризует изменение исследуемого явления во времени
Экономический индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.). Если в качестве базы сравнения используется уровень за какой-либо предшествующий период – получают динамический индекс; если же базой является уровень того же явления по другой территории - территориальный индекс. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или в пространстве две совокупности, элементы которых являются несоизмеримыми величинами. Изучение данной темы должно базироваться на знании предшествующих разделов курса, особенно тем «Формы выражения статистических показателей» и «Статистическое изучение динамики социально-экономических явлений». Индивидуальные индексы и сводные индексы в агрегатной форме. Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени (или в пространстве) отдельных элементов той или иной совокупности. Так, индивидуальный индекс цены рассчитывается по формуле
где р1 – цена товара в текущем периоде; р0 – цена товара в базисном периоде. Например, если цена товара А в текущем периоде составляла 30 руб., а в базисном 25 руб., то индивидуальный индекс цены
В данном примере цена товара А возросла по сравнению с базисным уровнем в 1, 2 раза, или на 20%. Оценить изменение объемов продажи товара в натуральных единицах измерения позволяет индивидуальный индекс физического объема реализации:
где q1 – количество товара, реализованное в текущем периоде; q0 – количество товара, реализованное в базисном периоде. Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:
Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики или темпы роста и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах. Сводный индекс – это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов. Исходной формой сводного индекса является агрегатная. При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Рассмотрим пример с розничными ценами. Цены различных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с экономической точки зрения вполне допустимо суммировать товарооборот по этим товарам. Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:
На величину данного индекса оказывают влияние как изменение цен на товары, так и изменение объемов их реализации. Длятого чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей, как цена себестоимость, производительность труда, урожайность, количественный показатель обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Паше)[1]:
Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает имевшее место изменение цен. Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных а в физических единицах измерения:
Весами в данном индексе выступают цены, которые фиксируются на базисном уровне. Между рассчитанными индексами существует следующая взаимосвязь: Ip · Iq = Ipq Пример. Имеются следующие данные о реализации плодово-ягодной продукции в области (табл. 12.1). Таблица 12.1 Реализация плодово-ягодной продукции в области
Рассчитать индекс товарооборота. Решение.
Мы получили, что товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3, 1% (100 – 96, 9)). Отметим, что объем товарной группы при расчете этого и последующих индексов значения не имеет. Вычислим сводный индекс цен:
По данной товарной группе цены в августе по сравнению с июлем в среднем снизились на 10, 8%. Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода («+») покупателей от изменения цен: Е = Σ p1q1 – Σ p0q0 = 618 – 693 = -75 тыс. руб. Индекс физического объема реализации составит:
Физический объем реализации (товарооборота) увеличился на 8, 6%. Используя взаимосвязь индексов, проверим правильность вычислений: Ipq = Iр · Iq = 0, 892 · 1, 086 = 0, 969, или 96, 9%. Мы рассмотрели применение агрегатных индексов в анализе товарооборота и цен. При анализе результатов производственной деятельности промышленного предприятия приведенные выше сводные индексы соответственно называются индексом стоимости продукции, индексом оптовых цен и индексом физического объема продукции. Рассмотрим применение индексного метода в анализе изменения затрат на производство и себестоимости продукции. Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным:
Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:
Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости: Е = Σ z1q1 – Σ z0q1. Сводный индекс физического объема продукции, взвешенный по себестоимости, имеет следующий вид:
Третьим показателем в данной индексной системе является сводный индекс затрат на производство:
Все три индекса взаимосвязаны между собой: Iz · Iq = Izq. Еще одна область применения индексного метода – анализ изменений в производительности труда. При этом возможны два подхода к расчету индексов. Первый подход основан на учете количества продукции, вырабатываемого в единицу времени (w). При таких расчетах необходимо решить ряд методологических проблем – какой именно показатель продукции использовать, как оценивать продукцию работников сферы услуг и пр. При втором подходе производительность труда определяется затратами рабочего времени на единицу продукции (t). На практике эти расчеты также сопряжены с определенными трудностями, так как не всегда имеется возможность оценить вклад конкретного работника в производство того или иного изделия. Количество продукции, вырабатываемое в единицу времени (в натуральном выражении), и затраты времени на единицу продукции взаимосвязаны между собой:
Например, если работник на каждое изделие затрачивает 15 мин. (t = 0, 25 ч), то за час его выработка составит 4 изделия. Отметим, что выработка может измеряться не только в натуральном, но в стоимостном выражении (pq). Индивидуальные индексы производительности труда, основанные на этих показателях, имеют следующий вид:
где Т – суммарные затраты времени на выпуск данной продукции в человеко-часах, человеко-днях или человеко-месяцах (в последнем случае соответствует общей численности работников). Трудоемкость является обратным показателем, поэтому снижение трудоемкости в текущем периоде по сравнению с базисным свидетельствует о росте производительности труда. Располагая данными о трудоемкости различных видов продукции и объемах их производства, можно рассчитать сводный индекс производительности труда (по трудоемкости):
Знаменатель этого индекса отражает реально имевшие место общие затраты времени на выпуск всей продукции в текущем периоде (Т1). Числитель представляет собой условную величину, показывающую, какими были бы затраты времени на выпуск этой продукции, если бы трудоемкость не изменилась. Пример. По данным табл. 12.2 измерим рост производительности труда на предприятии X.
Таблица 12.2 Трудоемкость и выпуск продукции на предприятии X
Рассчитать сводный индекс производительности труда по трудоемкости. Решение.
Мы получили, что прирост производительности труда в целом по предприятию составил 13, 9%. Индекс производительности труда по трудоемкости связан с индексом затрат рабочего времени (труда) и с индексом физического объема продукции, взвешенным по трудоемкости: Iw · IT = Iq или При расчете сводного индекса производительности труда в стоимостном выражении (по выработке) необходимо количество продукции, произведенной за каждый период, взвесить о каким-либо ценам, принятым за сопоставимые. В качестве сопоставимых могут выступать цены текущего, базисного или какого-либо другого периода или средние цены. Индекс в этом варианте рассчитывается по формуле
Первая часть этой формулы представляет собой среднюю выработку в отчетном периоде, вторая часть – в базисном. Пример. Предположим, имеются следующие данные о производстве продукции и отпускных ценах предприятия А (табл. 12.3). Таблица 12.3
Вычислить индекс производительности труда. Решение.
Итак, в текущем периоде за 1 чел-ч. вырабатывалось 65, 8 руб. продукции, а в базисном – 64, 4 руб. Прирост производительности труда составил 2, 2%. Умножение индекса производительности труда по выработке на индекс затрат рабочего времени приводит к индексу физического объема продукции, взвешенному по цене: Iw · IT = Iq или Сводные индексы в средней арифметической и средней гармонической формах. В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождествен исходному агрегатному индексу. Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (p1q1) и индивидуальными индексами цен
Таким образом, сводный индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:
Пример. По данным табл. 12.4 получите сводную оценку изменения цен. Таблица 12.4 Реализация овощной продукции
Решение. Вычислим средний гармонический индекс:
Цены по данной товарной группе в текущем периоде по сравнению с базисным в среднем возросли на 1, 6%. При расчете сводного индекса физического объема товарооборота q1 = iqq0. Тогда индекс примет вид:
Пример. Предположим, в нашем распоряжении имеются следующие данные (табл. 12.5). Таблица 12.5 Реализация товаров в натуральном и стоимостном выражениях
Рассчитать средний арифметический индекс. Решение.
Физический объем реализации данных товаров в среднем снизился на 3, 6%. В средней арифметической форме также может рассчитываться и индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина:
Системы индексов. Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме. Такая схема расчета индексов за несколько временных периодов называется системой индексов. В зависимости от информационной базы и целей исследователя индексная система может строиться в четырех вариантах. Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за «n» периодов: А. Цепные индексы цен с переменными весами:
Б. Цепные индексы цен с постоянными весами:
В. Базисные индексы цен с переменными весами:
Г. Базисные индексы цен с постоянными весами:
Индексы постоянного и переменного состава. Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в одном месте, или видам продукции, производимым на одном предприятии. Рассмотрим теперь случай, когда один товар реализуется в нескольких местах или вид продукции производится на ряде предприятий. Если реализуется только один вид продукции, вполне правомерно рассчитать его среднюю цену в каждом периоде. Индекс переменного состава представляет собой отношение двух полученных средних значений:
Данный индекс характеризует не только изменение индивидуальных цен в местах продажи, но и изменение структуры реализации по предприятиям розничной или оптовой торговли, рынкам, городам и регионам. Для оценки воздействия этого фактора рассчитывается индекс структурных сдвигов:
Последним в данной системе является рассмотренный выше индекс цен фиксированного состава, который не учитывает изменение структуры:
Между данными индексами существует следующая взаимосвязь:
Пример. Проведем анализ изменения цен реализации товара А в двух регионах (табл. 12.6). Таблица 12.6 Реализация товара А в двух регионах
Вычислим индекс цен переменного состава:
Из табл. 12.6 видно, что цена в каждом регионе в июле по сравнению с июнем возросла. В целом же средняя цена снизилась на 2, 2% (97, 8 – 100). Такое несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в июне по более высокой цене продавали товара вдвое больше, в июле же ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным). Рассчитаем индекс структурных сдвигов:
Первая часть этого выражения позволяет ответить на вопрос, какой была бы средняя цена в июле, если бы цены в каждом регионе сохранились на прежнем июньском уровне. Вторая часть отражает фактическую среднюю цену июня. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 10, 9%. Рассчитанный индекс цен фиксированного состава равен 1, 093, или 109, 8%. Отсюда следует вывод: если бы структура реализации товара А по регионам не изменилась, средняя цена возросла бы на 9, 8%. Однако влияние на среднюю цену первого фактора оказалось сильнее, что отражается в следующей взаимосвязи: 1, 098 · 0, 891 = 0, 978. Аналогично строятся индексы структурных сдвигов, переменного и фиксированного составов для анализа изменения себестоимости, урожайности и пр. Территориальные индексы. Территориальные индексы служат для сравнения показателей в пространстве, т.е. по предприятиям, округам, городам, районам и пр. Построение территориальных индексов определяется выбором базы сравнения и весов или уровня, на котором фиксируются веса. При двусторонних сравнениях каждая территория может быть и сравниваемой (числитель индекса), и базой сравнения (знаменатель). Веса как первой, так и второй территории в принципе также имеют равные основания использоваться при расчете индекса. Однако это может привести к различным или даже противоречивым результатам. Избежать подобной неопределенности можно несколькими способами. Один из них заключается в том, что в качестве весов принимаются объемы проданных товаров по двум регионам, вместе взятым: Q = qa + qb. Территориальный индекс цен в этом случае рассчитывается по следующей формуле:
Пример. Известны цены и объем реализации товаров по двум регионам (табл. 12.7). Таблица 12.7
Рассчитать территориальный индекс цен. Решение. . Цены в регионе В на 0, 2% превышают цены в регионе А. Этому выводу не противоречит и обратный индекс:
В формуле данного территориального индекса вместо суммарных иногда используются стандартизованные веса (стандартизованная структура). В качестве таких весов может выступать структура продажи данных видов продукции по более крупному территориальному образованию, например, республике. В этом случае индекс имеет вид:
Второй способ расчета территориальных индексов учитывает соотношение весов сравниваемых территорий. При этом способе первый шаг заключается в расчете средней цены каждого товара по двум территориям, вместе взятым:
После этого непосредственно рассчитывается территориальный индекс:
По данным нашего примера получим:
С учетом рассчитанных средних цен вычислим индекс:
Данный подход к расчету территориального индекса обеспечивает известную взаимосвязь: Ip · Iq = Ipq. Индекс физического объема реализации при этом строится следующим образом:
Аналогично строятся индексы для сравнения цен территории А с ценами территории Б.
|

 ,
, .
. ,
, .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.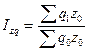 .
. .
. ;
; ,
, .
. .
. .
. .
. .
. .
. , полученными, например, в результате выборочного наблюдения. Тогда в знаменателе сводного индекса цен
, полученными, например, в результате выборочного наблюдения. Тогда в знаменателе сводного индекса цен  можно использовать следующую замену:
можно использовать следующую замену: .
. .
.
 .
. можно использовать среднюю арифметическую форму. При этом в числителе производится замена:
можно использовать среднюю арифметическую форму. При этом в числителе производится замена: .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.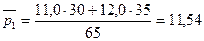 ;
; ;
; .
.
 .
.


