Методические указания и решение типовых задач. Изучаемые статистикой процессы и явления в сфере промышленного или сельскохозяйственного производства
Изучаемые статистикой процессы и явления в сфере промышленного или сельскохозяйственного производства, финансов, коммерции, демографии, в социальной и политической областях, как правило, характеризуются внутренней структурой, которая с течением времени может изменяться. Динамика структуры вызывает изменение внутреннего содержания исследуемых объектов и их экономической интерпретации, приводит к изменению установившихся причинно-следственных связей. Именно поэтому изучение структуры и структурных сдвигов занимает важное место в курсе теории статистики. Материал данной главы методологически связан с темами «Формы выражения статистических показателей» и «Ряды динамики», поэтому к его изучению можно приступать только после завершения работы над соответствующими главами. В статистике под структурой понимают совокупность единиц, обладающих определенной устойчивостью внутригрупповых связей при сохранении основных признаков, характеризующих эту совокупность как целое. Основные направления изучения структуры включают: а) характеристику структурных сдвигов отдельных частей совокупности за два и более периодов; б) обобщающую характеристику структурных сдвигов в целом по совокупности; в) оценку степени концентрации и централизации. Рассмотрим последовательно эти направления исследования. Частные показатели структурных сдвигов. Анализ структуры и ее изменений базируется на относительных показателях структуры – долях или удельных весах, представляющих собой соотношение размеров частей и целого. При этом как частные, так и обобщающие показатели структурных сдвигов могут отражать либо «абсолютное» изменение структуры в процентных пунктах или долях единицы (кавычки показывают, что данные показатели являются абсолютными по методологии расчета, но не по единицам измерения), либо ее относительное изменение в процентах или коэффициентах. Абсолютный прирост удельного веса i-й части совокупности показывает, на сколько процентных пунктов возросла или уменьшилась данная структурная часть в j-й период по сравнению с (j-1) периодом:
где dij – удельный вес (доля) i-й части совокупности в j-й период; dij-1 – удельный вес (доля) i-й части совокупности в j-l-й период. Знак прироста показывает направление изменения удельного веса данной структуры части («+» - увеличение, «-» - уменьшение), а его значение – конкретную величину этого изменения. Темп роста удельного веса представляет собой отношение удельного веса i-й части в j-й период времени к удельному весу той же части в предшествующий период:
Темпы роста удельного веса выражаются в процентах и всегда являются положительными величинами. Однако, если в совокупности имели место какие-либо структурные изменения, часть темпов роста будет больше 100%, а часть - меньше. Пример. Рассчитаем показатели частных структурных сдвигов по данным о распределении коммерческих банков по размеру объявленного уставного фонда (табл. 11.1). Решение. Как следует из данных табл. 11.1, наиболее существенно в «абсолютном» выражении изменился удельный вес банков с уставным фондом до 1 млрд. руб. Он снизился на 20, 2 проц. пункта. В относительном выражении наиболее сильно (в 3 раза) выросла доля банков с уставным фондом свыше 5 млрд. руб. Таблица 11.1
Мы рассмотрели показатели структурных сдвигов за один интервал между двумя периодами. Если же изучаемая структура представлена данными за три и более периода, появляется необходимость в динамическом осреднении приведенных выше показателей, т.е. в расчете средних показателей структурных сдвигов. Средний «абсолютный» прирост удельного веса i-й структурной части показывает, на сколько процентных пунктов в среднем за какой-либо период (день, неделю, месяц, год и т.п.) изменяется данная структурная часть:
где n – число осредняемых периодов. Сумма средних «абсолютных» приростов удельных весов всех k структурных частей совокупности, так же как и сумма их приростов за один временной интервал, должна быть равна нулю. Средний темп роста удельного веса характеризует среднее относительное изменение удельного веса i-й структурной части за n периодов и рассчитывается по формуле средней геометрической:
Подкоренное выражение этой формулы представляет собой последовательное произведение цепных темпов роста удельного веса за все временные интервалы. После проведения несложных алгебраических преобразований данная формула примет следующий вид:
Для иллюстрации этих формул воспользуемся приведенным выше примером (табл. 11.1). Рассчитаем средний месячный прирост (в данном случае – снижение) удельного веса банков 1-й группы:
По этой же группе определим средний месячный темп рос удельного веса:
Мы получили, что удельный вес банков данной группы в среднем ежемесячно снижался на 1, 8 проц. пункта, или на 3, 3% (96, 7% – 100%). При анализе структуры исследуемого объекта или явления за ряд периодов также можно определить средний удельный вес каждой i-й части за весь рассматриваемый временной интервал. Однако для его расчета одних лишь относительных данных об удельных весах структурных частей недостаточно, необходимо располагать еще и информацией о размерах этих частей в абсолютном выражении. Используя эти данные, средний удельный вес любой i-й структурной части можно определить по формуле
где Хij – величина i-й структурной части в j-й период времени в абсолютном выражении. Пример. По данным первичного рынка государственных краткосрочных облигаций (ГКО) и облигаций федерального займа (ОФЗ) в III квартале 1995 г. определим средний удельный вес ценных бумаг каждого вида в общем объеме выручки от их реализации (табл. 11.2). Таблица 11.2 Выручка от реализации ГКО и ОФЗ
Решение. Определим средний удельный вес выручки от продажи ГКО общем объеме выручки от реализации государственных ценных бумаг:
Рассчитаем средний удельный вес выручки от продажи ОФЗ:
Итак, в июле-сентябре 1995 г. на долю ГКО в среднем приходилось 94, 3% общего объема выручки от реализации государственных ценных бумаг, на долю ОФЗ – только 5, 7%. Обобщающие показатели структурных сдвигов. В отдельных случаях исследователю необходимо в целом оценить структурные изменения в изучаемом социально-экономическом явлении за определенный временной интервал, которые характеризуют подвижность или, наоборот, стабильность, устойчивость данной структуры. Как правило, это требуется для сравнения динамики одной и той же структуры в различные периоды или нескольких структур, относящихся к разным объектам. Во втором случае число структурных частей у разных объектов необязательно должно совпадать. Среди применяемых для этой цели обобщающих показателей наиболее распространен линейный коэффициент «абсолютных» структурных сдвигов, представляющий собой сумму приростов удельных весов, взятых по модулю, деленную на число структурных частей:
Этот показатель отражает то среднее изменение удельного веса (в процентных пунктах), которое имело место за рассматриваемый временной интервал в целом по всем структурным частям совокупности. Для решения данной задачи также применяют квадратический коэффициент «абсолютных» структурных сдвигов, который рассчитывается по формуле:
Линейный и квадратический коэффициенты «абсолютных» структурных сдвигов позволяют получить сводную оценку скорости изменения удельных весов отдельных частей совокупности. Для сводной характеристики интенсивности изменения удельных весов используется квадратический коэффициент относительных структурных сдвигов:
Данный показатель отражает тот средний относительный прирост удельного веса (в процентах), который наблюдался за рассматриваемый период. Пример. По данным табл. 11.3 рассчитаем обобщающие показатели структурных сдвигов:
Таблица 11.3 Структура использования денежных доходов населения РФ в IV квартале 1995 г.
Решение. Для расчета линейного коэффициента «абсолютных» структурных сдвигов за первый (с октября по ноябрь) и второй (с ноября по декабрь) периоды соответственно воспользуемся данными итогов граф 4, 7 табл. 11.3:
Итак, с октября по ноябрь 1995 г. удельный вес отдельных направлений использования доходов населения изменился в среднем на 1, 5 проц. пункта. С ноября по декабрь «абсолютные» структурные сдвиги заметно увеличились. Этот вывод подтверждается квадратическими коэффициентами «абсолютных» структурных сдвигов (необходимые промежуточные расчеты выполнены в графах 5, 8 табл. 11.3):
Далее определим величину квадратических коэффициентов относительных структурных сдвигов, воспользовавшись итоговыми данными граф 6, 9 табл. 11.3:
Расчеты показывают, что если в ноябре удельный вес каждой статьи расходов в среднем изменился более чем на треть своей величины, то в декабре – менее чем на четверть. Для сводной оценки структурных изменений в исследуемой совокупности в целом за рассматриваемый временной интервал, охватывающий несколько недель, месяцев, кварталов или лет, наиболее удобным является линейный коэффициент «абсолютных» структурных сдвигов за n периодов:
Используя итоговые данные гр. 10 табл. 11.3, получим:
Таким образом, за рассматриваемый период среднемесячное изменение по всем направлениям использования доходов составило 1, 8 проц. пункта. Необходимо отметить, что последний показатель может использоваться как для сравнения динамики двух и более структур, так и для анализа динамики одной и той же структуры за разные по продолжительности периоды времени. Показатели концентрации и централизации. Одна из задач статистического анализа структуры заключается в определении степени концентрации изучаемого признака по единицам совокупности или в оценке неравномерности его распределения. Такая неравномерность может иметь место в распределении доходов по группам населения, жилой площади по группам семей, прибыли по группам предприятий и т.д. При исследовании неравномерности распределения изучаемого признака по территории понятие «концентрация» обычно заменяется понятием «локализация». Оценка степени концентрации наиболее часто осуществляется по кривой концентрации (Лоренца) и рассчитываемым на ее основе характеристикам. Для построения кривой концентрации необходимо иметь частотное распределение единиц исследуемой совокупности и соответствующее ему частотное распределение изучаемого признака. При этом для удобства вычислений и повышения аналитичности данных единицы совокупности, как правило, разбиваются на равные группы – 10 групп по 10% единиц в каждой, 5 групп – по 20% единиц и т.д. Наиболее известным показателем концентрации является коэффициент Джини, обычно используемый как мера дифференциации или социального расслоения:
где dxi – доля i-й группы в общем объеме совокупности; dyi – доля i-й группы в общем объеме признака;
Если доли выражены в процентах, данную формулу можно преобразовать: для 10%-ного распределения –
для 20%-ного распределения –
Чем ближе к 1 (100%) значение данного показателя, тем выше уровень концентрации; при нуле мы имеем равномерное распределение признака по всем единицам совокупности. Оценка степени концентрации также может быть получена на основе коэффициента Лоренца:
При использовании данного коэффициента можно оперировать как долями единицы, так и процентами. Коэффициент Лоренца изменяется в тех же границах, что и коэффициент Джини. Пример. Определим степень концентрации доходов населения по данным табл. 11.4.
Таблица 11.4 Распределение доходов населения России в январе-сентябре 1995 г.
Для расчета коэффициента Джини воспользуемся итоговыми данными граф 4, 6 табл. 11.4: G = 1 – 2 · 0, 4108 + 0, 2 = 0, 378, или 37, 8%. Такой же результат мы получим, выполнив расчеты в процентах: G = 120 – 0, 4 (5, 5 + 15, 7 + 30, 9 + 53, 3 + 100, 0) = 37, 8%. Второй способ расчета проще; однако исходная формула незаменима в тех случаях, когда имеются неравные группы по объему совокупности (в нашем примере – по численности населения). Используя данные гр. 7 табл. 11.4, определим коэффициент Лоренца:
Оба коэффициента указывают на относительно высокую степень концентрации доходов населения. Если под концентрацией понимается степень неравномерности распределения изучаемого признака, не связанная ни с объемом совокупности, ни с численностью отдельных групп, то централизация означает сосредоточение объема признака у отдельных единиц (объема продукции данного вида на отдельных предприятиях, капитала в отдельных банках и т.п.). Обобщающий показатель централизации имеет следующий вид:
где mi – значение признака i-й единицы совокупности; М – объем признака всей совокупности. Максимальное значение, равное 1, данный коэффициент достигает лишь в том случае, когда совокупность состоит только из одной единицы, обладающей всем объемом признака. Минимальное значение коэффициента приближается к нулю, но никогда его не достигает. Пример. Выпуск продукции А сконцентрирован на пяти предприятиях, расположенных в трех районах области:
Вычислить показатель централизации производства данного вида продукции. Решение. IZ = 0, 5842 + 0, 1332 + 3 · 0, 0942 = 0, 39. Рассчитанная величина свидетельствует о высокой степени централизации. Отметим, что аналитическая ценность показателей концентрации и централизации повышается при проведении сравнений во временном или территориальном аспекте.
|

 ,
, .
.

 ,
, .
. .
.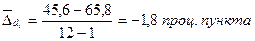 .
. .
. ,
, .
. .
. .
. .
.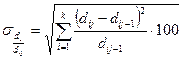 .
.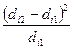

 ;
; .
.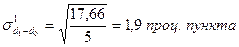 ;
; .
. ;
; .
. .
. .
. ,
, – накопленная доля i-й группы в общем объеме признака.
– накопленная доля i-й группы в общем объеме признака.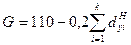 ;
; .
. .
. .
. ,
,


