Метод скользящей средней. .
В результате обработки ряда динамики методом скользящей средней проявилась тенденция к росту потребления овощей. 2. Метод аналитического выравнивания ряда динамики по прямой. Уравнение прямой имеет вид где а0 и а1 –параметры прямой t- показатель времени (дни, месяцы, годы и т. д.) Для нахождения параметров
где у – фактические уровни ряда динамики, n – число уровней. Для упрощения расчетов обозначим время так, чтобы начало его отсчета приходилось на середину рассматриваемого периода. Таблица 20 Расчетные данные для определения параметров системы нормальных уравнений и выровненных теоретических значений (
Так как Отсюда Уравнение прямой будет иметь вид Подставив в это уравнение значение t), получим выровненные теоретические значения Параметры
Приведенные формулы показывают, что для нахождения параметров а0 иа1необходимо получить следующие значения: Обозначив годы (t) порядковыми номерами, определим эти величины и представим их значения в таблице 42.
Таблица 21
|





 33, 0
33, 0  35, 2
35, 2  39, 5...
44.8...
49, 7…
51, 4
39, 5...
44.8...
49, 7…
51, 4  -
-
 11, 0
11, 0  11, 8
11, 8  13, 2…
15, 9…
17, 1
13, 2…
15, 9…
17, 1 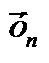 -
-


 необходимо решить систему нормальных уравнений
необходимо решить систему нормальных уравнений
 )
)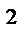

 =123.6
=123.6
 =0
=0
 =60
=60
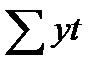 =66.5
=66.5
 =123.66
=123.66







