Расчет сумм вычисления параметров уравнения прямой по несгруппированным данным
Подставим в систему нормальных уравнений фактические данные из таблицы. И получим равенства
Систему нормальных уравнений решаем в такой последовательности (по методу множителей): умножим каждый член первого уравнения на число, равное 5, получим
Затем вычтем из второго уравнения первое: После постановки значения a1 в первое уравнение получим С помощью определителей параметры уравнения прямой можно вычислить по формулам. Если параметры регрессионного уравнения определены верно, то должно соблюдаться равенство сумм теоретических и эмпирических значений выпуска готовой продукции, а сумма разностей между эмпирическими и теоретическими значениями выпуска готовой продукции должна быть равна нулю. Окончательную проверку правильности расчета параметров уравнения связи можно также произвести подстановкой а0 и а1 в систему нормальных уравнений. Используя уравнения корреляционной связи, можно определить теоретическое значения yx для любой промежуточной точки (теоретическое значение выпуска готовой продукции на одного рабочего дня любого промежуточного значения электровооруженности труда на одного рабочего) В нашем уравнении регрессии параметр а1=0, 796 показывает, что с увеличением электровооруженности труда одного рабочего на 1 кВт.ч выпуск готовой продукции возрастает на 0, 796 т. Средний коэффициент эластичности исчислим по формуле: Коэффициент эластичности, равной 0, 66, показывает, что с увеличением электровооруженности труда на 1 % выпуск готовой продукции возрастет на 0, 66%. Измерим тесноту корреляционной связи между производительностью и электровооруженности труда линейным коэффициентом корреляции, теоретическим корреляционным отношением, индексом корреляции, которые рассчитываются по формулам. Данные, необходимые для расчета этих показателей, представлены в таблице.
Для расчета теоретического корреляционного отношения необходимо предварительно вычислить дисперсии
Теоретическое корреляционное отношение по формуле равно:
Коэффициент детерминации
Все показатели тесноты корреляционной связи показывают тесную связь между производительностью и электровооруженностью труда. Коэффициент детерминации 0, 856 означает, что вариация выработки рабочих на 85, 6% объясняется вариацией электровооруженности труда и на 14, 4 %- прочими факторами. Так как r=R= Проведем оценку адекватности регрессионной модели ух=2, 02+0, 796х, выражающий зависимость между производительностью труда, с помощью F-критерия Фишера- формула:
Табличные значения Fтc уровнем значимости 0, 05 и числом степеней свободы равно 5, 32. Так как Fэ> Fт, то уравнение регрессии можно признать адекватным. Оценим значимость параметров уравнения регрессии с помощью t-критерия Стьюдента по формулам: ta0=2, 02 ta1=0.796 Значение
Табличное значение t-критерия с уровнем значимости 0, 05 и числом степени свободы (n-2) равно 2, 301. Так как tэмп> tтабл, то параметры уравнения регрессии можно признать значимыми. Значимость коэффициента корреляции оценим с помощью t-критерия по формуле
Так как параметры уравнения регрессии значимы, уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 5, 8%, коэффициент детерминации равен 0, 856, то можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от его электровооруженности ух=2, 02+0, 796х может быть использована для анализа и прогноза.
|


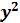





 , откуда
, откуда 



 ,
,  ,
, , по формулам
, по формулам у2=
у2= 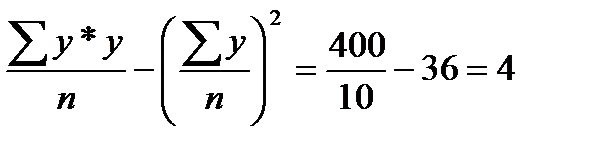



 равен 0, 856. Индекс корреляции по формуле:
равен 0, 856. Индекс корреляции по формуле: R=
R= 
 , то можно сделать заключение, что гипотеза о линейной форме связи подтверждена.
, то можно сделать заключение, что гипотеза о линейной форме связи подтверждена.


 вычисляется по формуле:
вычисляется по формуле: =
= 






