Событие-. № 8. На одинаковых карточках в троичной системе счисления записаны целые числа от 1 до 15
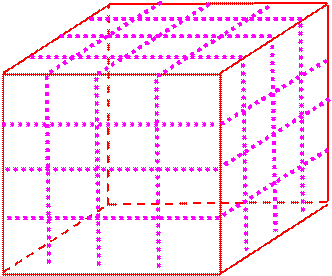
№ 8. На одинаковых карточках в троичной системе счисления записаны целые числа от 1 до 15. Наудачу извлекается одна карточка. Какова вероятность того, что записанное на ней число содержит: а) не менее двух единиц; б) хотя бы одну двойку; в) один нуль? Испытание- Событие- № 9. Какова вероятность того, что число на вырванном наудачу листке нового календаря: а) кратно пяти; б) равно 29, если в году 365 дней? Испытание- Событие- № 10. Из полной игры лото наудачу извлекается один бочонок. На бочонках написаны числа от 1 до 90 включительно. Какова вероятность того, что на извлеченном бочонке написано простое число? Испытание- Событие- № 11. В коллекции 200 монет, из которых 25 монет XVIII века. Какова вероятность того, что наудачу выбранная монета датирована XVIII веком? Испытание- Событие- № 12. Какова вероятность того, что кость, наудачу извлеченная из полного набора домино, имеет сумму очков, равную пяти? Испытание- Событие- № 13. В группе 6 юношей и 18 девушек. По жребию разыгрывается один билет в театр. Какова вероятность того, что билет получит девушка? Испытание- Событие- № 14. Куб, все грани которого окрашены, распилен на 64 кубика одинакового размера. Определите вероятность того, что извлеченный наудачу кубик будет иметь ровно две окрашенные грани.
Геометрическое определение № 15. Электрический провод, соединяющий пункты А и В, порвался в неизвестном месте. Чему равна вероятность того, что разрыв произошел не далее 500 м от пункта А, если расстояние между пунктами 2 км? Испытание-
|