ВВЕДЕНИЕ. В последние годы, особенно после введения для школьников обязательного ЕГЭ по математике, уровень довузовского математического образования заметно упал
В.А.Левашов
В последние годы, особенно после введения для школьников обязательного ЕГЭ по математике, уровень довузовского математического образования заметно упал. Данное обстоятельство существенно снижает эффективность изучения университетских математических курсов, а также тех курсов, которые активно используют математические знания. Подобные реалии жизни обязывают руководства факультетов, особенно тех, где математическая составляющая образовательного процесса составляет значительную часть, вводить в учебные планы направлений и специальностей корректирующие курсы по элементарной математике. Данное учебно-методическое пособие создано на основе реакции на возникшее обстоятельство и призвано ликвидировать многие пробелы в элементарной математике у поступивших на первый курс математического факультета абитуриентов, а также повысить уровень их мышления. Предлагаемое пособие рассчитано на годовой курс практикума по элементарной математике в объеме одного занятия в неделю. Пособие содержит материал 30 занятий, условно разбитых на две части: первая часть в объеме 14 занятий составляет материал первого семестра, вторая часть в объеме оставшихся 16 занятий составляет материал второго семестра. Первая часть содержит наиболее простые задачи курса, вторую часть составляют задачи более высокого уровня сложности – в этом состоит их основное отличие. Часть задач в пособии снабжена подробными решениями. Окончание решения конкретной задачи обозначается символом #. В пособии приводятся также основные формулы (они выделяются синим цветом), напоминаются некоторые определения (они выделяются зеленым цветом), приводится ряд утверждений и рекомендаций для решения задач (они выделяются красным цветом). По ходу обучения студентам предстоит выполнение 4 обязательных контрольных работ: по 2 работы в каждом семестре. Результаты контрольных работ будут образовывать основную составляющую семестрового зачета, обязательного для каждого студента первого курса. Все контрольные работы будут соответствовать пройденному на соответствующий момент материалу, как по составу, так и по сложности включенных в них задач. 1 задание 1) Решение задач первой части данного задания основано на понятии модуля (или абсолютной величины) Пример 1. Решить уравнение: Решение. По определению модуля действительного числа имеем:
Если уравнение содержит более одного модуля, то при его решении можно использовать разбиение действительной прямой на минимальное число промежутков, в каждом из которых функции, стоящие под знаками всех модулей, имеют значения только одного знака (метод интервалов). Этот прием позволяет уменьшить число рассматриваемых случаев, по сравнению с классическим вариантом. Если уравнение содержит два модуля, то при использовании данного приема придется рассматривать не более трех случаев, а в классическом варианте решения – четыре, если уравнение содержит три модуля, то придется рассматривать не более четырех случаев, а в классическом варианте решения – восемь и т.д. Пример 2. Решить уравнение: Решение. Функция, стоящая под первым модулем, меняет свой знак в точке
Решить уравнения: 1) 5) 8) 11) 14) 2) Вторая часть задания содержит задачи по планиметрии. Пример 3. В окружности радиуса Решение. Для решения задачи необходимо выполнить рисунок (рассмотрим два варианта):
Здесь 17) Сторона правильного треугольника, вписанного в окружность, равна 18) В прямоугольном треугольнике 19) В равнобедренном треугольнике основание равно 30см, а высота, на него опущенная, равна 20см. Определите длину высоты, опущенной на боковую сторону. 20) Вычислите длину стороны равностороннего треугольника, если разность между стороной этого треугольника и его высотой равна 2 задание 1) При решении неравенств можно использовать метод интервалов. Решить неравенства: 1) 5) 9) 12) 2) Вторая часть задания содержит задачи на арифметическую и геометрическую прогрессию. Напомним, что арифметической прогрессией называется упорядоченный набор из Пример 1. Три числа составляют геометрическую прогрессию. Если ко второму числу прибавить 8, то эти числа составят арифметическую прогрессию. Если затем к третьему числу прибавить 64, то полученные числа снова составят геометрическую прогрессию. Найдите эти три числа. Решение. По условию числа
Таким образом, получаем два набора искомых чисел: Решить задачи: 15) Между числом 3 и неизвестным числом вставлено еще одно число так, что все три числа образуют арифметическую прогрессию. Если средний член уменьшить на 6, то получится геометрическая прогрессия. Найдите неизвестное число. 16) Сумма трех положительных чисел, составляющих арифметическую прогрессию, равна 15. Если к этим числам прибавить соответственно 1, 4 и 19, то получится геометрическая прогрессия. Найдите эти числа. 17) Три положительных числа образуют арифметическую прогрессию. Третье число больше первого на 14. Если к третьему числу прибавить первое, а остальные два оставить без изменения, то получится геометрическая прогрессия. Найдите эти числа. 18) Три числа составляют геометрическую прогрессию. Если третий член уменьшить на 64, то полученные три числа составят арифметическую прогрессию. Если затем второй член этой прогрессии уменьшить на 8, то получится геометрическая прогрессия. Определите эти числа. 19) Первый и третий члены арифметической прогрессии соответственно равны первому и третьему членам геометрической прогрессии, а второй член арифметической прогрессии превышает второй член геометрической прогрессии на 0, 25. Вычислите сумму первых пяти членов арифметической прогрессии, если ее первый член равен 2. 20) Три числа образуют геометрическую прогрессию. Если среднее из них удвоить, то получится арифметическая прогрессия. Определите знаменатель данной прогрессии. 3 задание 1) При решении систем алгебраических уравнений могут оказаться полезными известные со школы формулы сокращенного умножения и формулы разложения на элементарные множители:
Решить системы: 1) 4) 7) 11) 2) Вторая часть задания содержит задачи по планиметрии. Пример 1. В треугольнике Решение. Изобразим схематично заданный треугольник:
По условию задачи можно положить Решить задачи: 15) Чему равны длины высот треугольника и площадь описанного около него круга, если стороны треугольника задаются уравнениями: 16) Чему равны длины высот и площадь круга, вписанного в треугольник, стороны которого заданы уравнениями: 17) В равнобедренную трапецию вписана окружность радиуса 3см. Найти расстояние между точками касания этой окружности с боковыми сторонами трапеции, если одно из ее оснований равно 18) В прямоугольный треугольник вписана окружность. Гипотенуза делится точкой касания на отрезки длиной 5см и 12см. Найдите площадь треугольника. 19) В прямоугольный треугольник, периметр которого равен 36см, вписана окружность. Гипотенуза делится точкой касания в отношении 2: 3. Найдите длины сторон треугольника. 20) В треугольнике АВС высота CD= 7, высота АЕ= 6. Точка Е лежит на стороне ВС и ВЕ: СЕ= 3: 4. Найдите длину стороны АВ. 4 задание 1) При решении иррациональных уравнений необходимо помнить о возможности приобретения посторонних корней, поэтому в завершающей части решений нужно делать проверку найденных корней или по ходу решения использовать области определения уравнений. Пример 1. Решить уравнение: Решение. Имеем:
Решить уравнения: 1) 2) Вторая часть задания содержит задачи на движение тел. Решение таких задач сводится к решению уравнений или их систем, при составлении которых часто в качестве неизвестных берется скорость движения этих тел. Пример 2. Если пароход и катер плывут по течению реки, то расстояние от пункта Решение. Обозначим за
Решить задачи: 16) Поезд вышел со станции А по направлению к станции В. Пройдя 450км, что составляло 75% всего пути от А до В, поезд остановился. Через полчаса движение возобновилось, и машинист, увеличив скорость поезда на 15км/ч, привел его на станцию В без опоздания. Найдите начальную скорость поезда. 17) Автомобиль выехал из города А в город В, расстояние между которыми 234км. Через час из города В навстречу ему выехал автомобиль, проезжавший в час на 12км больше первого. Определите скорость каждого автомобиля, если они встретились на расстоянии 108км от города В. 18) Два поезда вышли из города А в город В. Весь путь каждый из поездов прошел с постоянной скоростью. Второй поезд вышел на 5 ч позже первого и прибыл в В одновременно с первым поездом. За один час до прибытия в В расстояние между поездами составляло 30км, а когда первый поезд находился в середине пути, второй отставал от него на 225км. Определите скорости поездов и расстояние между городами А и В. 19) Моторная лодка прошла вниз по течению реки 14км, а затем 9км против течения, затратив на весь путь 5 ч. Найдите скорость течения реки, если скорость моторной лодки в стоячей воде равна 5км/ч. 20) Лодка спускается вниз по течению реки из пункта А в пункт В, находящийся в 10км от А, а затем возвращается в А. Если собственная скорость лодки 3км/ч, то путь из А в В занимает на 2 ч 30 мин меньше, чем из В в А. Какой должна быть собственная скорость лодки, чтобы поездка из А в В заняла 2 ч? 5 задание 1) При решении неравенств проверку найденных решений, как правило, выполнить не удается, поэтому здесь приходится опираться лишь на области определения неравенств. Среди иррациональных неравенств наиболее часто применяются два типа неравенств. Пример 1. Решить неравенство: Решение. Имеем:
Пример 2. Решить неравенство: Решение. Имеем:
Решить неравенства: 1) 10) 2) Вторая часть задания содержит задачи по планиметрии. Пример 3. Медианы треугольника равны 13, 14 и 15см. Найдите площадь треугольника. Решение. Опираясь на известную теорему о том, что все медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении
Четырехугольник
так что Решить задачи: 14) Биссектриса одного из углов параллелограмма делит его диагональ на отрезки длиной 4см и 6см. Найти периметр параллелограмма, если одна из его сторон равна 24см. 15) Точка, взятая на гипотенузе прямоугольного треугольника и одинаково удаленная от его катетов, делит гипотенузу на отрезки, длины которых равны 40см и 30см. Найти катеты треугольника. 16) Из точки проведены две касательные к окружности, длиной 5см каждая. Расстояние между точками касания равно 6см. Найдите радиус окружности. 17) Стороны треугольника равны 13см, 14см и 15см. Две меньшие из них служат касательными к окружности, центр которой лежит на третьей стороне. Найти длину окружности. 18) Окружность, построенная на стороне 19) В острый угол, равный 60 20) В параллелограмме 6 задание 1) При решении уравнений, содержащих показательные функции, могут быть полезны следующие известные формулы:
Решить уравнения и системы уравнений: 1) 8) 12) 2) При решении задач на работу полезно помнить о том, что они близки по духу с задачами на движение: пройденный путь – это объем выполненной работы, а скорость движения – это производительность труда, т.е. объем выполненной работы за единицу времени. Пример 1. Бригада рабочих должна была за определенный срок изготовить 400 деталей. В течение первых пяти дней бригада перевыполняла дневную норму на 20%, а в последующие дни изготовляла ежедневно 15 деталей сверх плана и уже за два дня до срока изготовила 405 деталей. Сколько деталей должна была ежедневно изготавливать бригада по плану? Решение. Пусть
Очевидно, условию задачи удовлетворяет Решить задачи: 15) Три тракторные бригады вместе вспахивают поле за 4 дня. Первая и вторая бригады вместе вспахали бы это поле за 6 дней, а первая и третья вместе – за 8 дней. Во сколько раз вторая бригада вспахивает за один день больше, чем третья? 16) Три обыкновенных и два тракторных плуга обрабатывают вместе поле за 6 дней. Три тракторных плуга выполнили бы ту же работу на 5 дней быстрее, чем девять обыкновенных. Во сколько раз производительность тракторного плуга больше производительности обыкновенного? 17) На обработку одной детали первый рабочий затрачивает на 6 мин меньше, чем второй. Сколько деталей обрабатывает каждый из них за 7 ч, если первый обрабатывает за это время на 8 деталей больше другого? 18) Двое рабочих, работая одновременно, выполнили всю работу за 5 дней. Если бы первый работал вдвое быстрее, а второй – вдвое медленнее, то работа заняла бы у них 4 дня. За сколько времени выполнил бы всю работу один первый рабочий? 19) Каждому из трех рабочих для выполнения некоторой работы требуется определенное время, причем третий рабочий выполняет ее на 1ч быстрее первого. Работая все вместе, они выполняют работу за один час. Если же первый рабочий проработает 1ч, то второму для завершения всей работы потребуется 4ч. За какое время может выполнить всю работу каждый рабочий? 20) Трое рабочих должны сделать 80 одинаковых деталей. Известно, что вместе они делают за час 20 деталей. К работе приступил сначала первый рабочий. Он сделал 20 деталей, затратив на это более 3ч. Оставшуюся часть работы выполнили вместе второй и третий рабочие. На всю работу было затрачено 8ч. Сколько часов потребовалось бы первому рабочему на всю работу, если бы с начала и до конца он делал ее один? 7 задание 1) При решении уравнений, содержащих логарифмические функции, часто используются следующие известные формулы:
Решить урав
|

 действительного числа
действительного числа  . Напомним, что
. Напомним, что 
 .
. . #
. # .
. , под вторым – в точке
, под вторым – в точке  , а под третьим – в точке
, а под третьим – в точке  . Поэтому разбиваем действительную прямую на 4 промежутка, на каждом из них определяем знаки функций, стоящих под модулями, и сводим решение уравнения к решению системы:
. Поэтому разбиваем действительную прямую на 4 промежутка, на каждом из них определяем знаки функций, стоящих под модулями, и сводим решение уравнения к решению системы:











 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  ;
;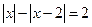 ; 9)
; 9) 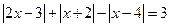 ; 10)
; 10)  ;
; ; 12)
; 12)  ; 13)
; 13)  ;
;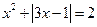 ; 15)
; 15)  ; 16)
; 16) 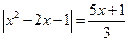 .
. проведена хорда длиной
проведена хорда длиной  , где
, где  . Через один конец хорды проведена касательная к этой окружности, а через другой конец – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.
. Через один конец хорды проведена касательная к этой окружности, а через другой конец – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.





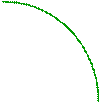

















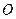
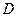
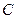
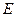
 ,
,  ,
, 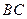 - касательная к окружности, поэтому
- касательная к окружности, поэтому  ,
,  . Следовательно, искомое расстояние -
. Следовательно, искомое расстояние -  . В равнобедренном
. В равнобедренном  проведем высоту
проведем высоту  . Из рисунка видно, что
. Из рисунка видно, что  (эти треугольники - прямоугольные и имеют общий острый
(эти треугольники - прямоугольные и имеют общий острый  ). Поэтому
). Поэтому  . Так как
. Так как  , то
, то  . # Решить задачи:
. # Решить задачи: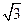 см. Найти площадь квадрата, вписанного в эту же окружность.
см. Найти площадь квадрата, вписанного в эту же окружность. угол
угол  , а радиус описанной около треугольника
, а радиус описанной около треугольника  м. Найти длину радиуса вписанной в треугольник
м. Найти длину радиуса вписанной в треугольник  м.
м. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 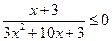 ;
; ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ;
; ; 10)
; 10)  ; 11)
; 11)  ;
; ; 13)
; 13)  ; 14)
; 14)  .
. действительных чисел вида
действительных чисел вида  ,
,  ,
,  , …,
, …,  . Число
. Число  называется разностью прогрессии. При решении задач часто используется характеристическое свойство арифметической прогрессии: для любых трех последовательных членов арифметической прогрессии
называется разностью прогрессии. При решении задач часто используется характеристическое свойство арифметической прогрессии: для любых трех последовательных членов арифметической прогрессии  ,
,  и
и  среднее из них равно среднему арифметическому крайних членов:
среднее из них равно среднему арифметическому крайних членов: 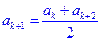 . Геометрической прогрессией называется упорядоченный набор из
. Геометрической прогрессией называется упорядоченный набор из  ,
,  , …,
, …,  . Число
. Число 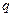 называется знаменателем прогрессии. При решении задач часто используют характеристическое свойство геометрической прогрессии: для любых трех последовательных членов геометрической прогрессии
называется знаменателем прогрессии. При решении задач часто используют характеристическое свойство геометрической прогрессии: для любых трех последовательных членов геометрической прогрессии  ,
,  и
и 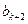 квадрат среднего из них равен произведению крайних членов:
квадрат среднего из них равен произведению крайних членов:  .
. ,
,  и
и  образуют геометрическую прогрессию, числа
образуют геометрическую прогрессию, числа  и
и  вновь образуют геометрическую прогрессию. Используя характеристические свойства прогрессий, получаем систему двух уравнений:
вновь образуют геометрическую прогрессию. Используя характеристические свойства прогрессий, получаем систему двух уравнений:
 ,
,  ,
, 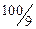 и
и  ,
,  ,
, 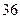 . #
. # ,
,  ,
, 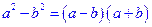 ,
, ,
,  ,
, ,
,  .
. 2)
2)  3)
3) 
 5)
5) 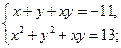 6)
6) 
 8)
8)  9)
9)  10)
10) 
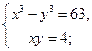 12)
12)  13)
13)  14)
14) 
 ,
,  . Точка
. Точка  . Найдите длину стороны
. Найдите длину стороны  .
.






 и
и 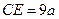 . Тогда
. Тогда  , так что
, так что  . Из полученного равенства находим:
. Из полученного равенства находим:  . Применим теперь теорему Пифагора к
. Применим теперь теорему Пифагора к  :
:  , откуда получаем
, откуда получаем 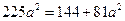 и
и  . Следовательно,
. Следовательно,  . #
. # ;
;  ;
;  .
. ;
;  ;
;  .
. см.
см.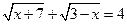 .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 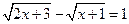 ; 6)
; 6) 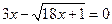 ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14) 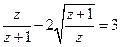 ; 15)
; 15)  .
.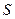 расстояние между пунктами
расстояние между пунктами 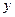 - скорости парохода и катера в стоячей воде. Из условия задачи следует, что скорость течения реки составляет 8 км/час. Условия задачи можно записать в виде системы двух уравнений:
- скорости парохода и катера в стоячей воде. Из условия задачи следует, что скорость течения реки составляет 8 км/час. Условия задачи можно записать в виде системы двух уравнений: #
# .
. . #
. # .
. #
#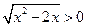 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 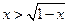 ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7) 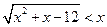 ; 8)
; 8)  ; 9)
; 9)  ;
;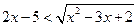 ; 11)
; 11)  ; 12)
; 12)  ; 13)
; 13)  .
. , считая от вершины угла, проведем дополнительное построение: продолжим медиану
, считая от вершины угла, проведем дополнительное построение: продолжим медиану  за точку
за точку  , и точку
, и точку  соединим с точками
соединим с точками 





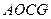 будет параллелограммом, так как его диагонали
будет параллелограммом, так как его диагонали  делятся пополам точкой
делятся пополам точкой  , а треугольники
, а треугольники  и
и  имеют одинаковую высоту, то
имеют одинаковую высоту, то  . Но
. Но  , поэтому
, поэтому  . Стороны треугольника
. Стороны треугольника  ,
,  и
и  см, поэтому по формуле Герона
см, поэтому по формуле Герона  , где
, где  ,
,  - длины сторон треугольника, а
- длины сторон треугольника, а  - его полупериметр. Следовательно,
- его полупериметр. Следовательно, ,
, . #
. #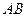 в точке
в точке 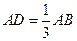 . Найти площадь треугольника
. Найти площадь треугольника  .
.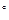 , вписаны две окружности, внешним образом касающиеся друг друга. Радиус меньшей окружности 2см. Найдите радиус большей окружности.
, вписаны две окружности, внешним образом касающиеся друг друга. Радиус меньшей окружности 2см. Найдите радиус большей окружности. длина диагонали
длина диагонали  , причем
, причем  касается окружности, описанной около треугольника
касается окружности, описанной около треугольника 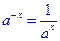 ,
,  ,
,  ,
, 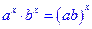 ,
,  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ;
; ; 9)
; 9)  ; 10)
; 10)  11)
11) 
 13)
13)  14)
14) 
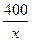 - планируемое время выполнения задания. Производительность бригады за первые 5 дней составила
- планируемое время выполнения задания. Производительность бригады за первые 5 дней составила  , а в оставшиеся дни работы она была
, а в оставшиеся дни работы она была  . Условие задачи можно записать в виде уравнения:
. Условие задачи можно записать в виде уравнения:
 . Это и является ответом на поставленную задачу. #
. Это и является ответом на поставленную задачу. #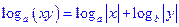 ,
,  ,
,  ,
,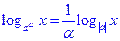 ,
,  ,
,  .
.


