11) 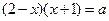 ; 12)
; 12) 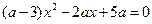 .
.
13) При каких  корни уравнения
корни уравнения  будут неотрицательными (неположительными) действительными числами?
будут неотрицательными (неположительными) действительными числами?
14) Для каких 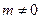 один из действительных корней уравнения
один из действительных корней уравнения  равен удвоенному действительному корню уравнения
равен удвоенному действительному корню уравнения 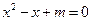 ?
?
15) Для каких действительных чисел  действительные корни уравнения
действительные корни уравнения 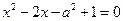 лежат между действительными корнями уравнения
лежат между действительными корнями уравнения 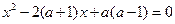 ?
?
2) Во второй части задания приведены задачи по стереометрии.
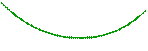
Пример 2. Центр сферы совпадает с центром основания кругового конуса, а ее радиус равен радиусу основания конуса. Длина образующей конуса равна 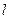 , а угол его осевого сечения равен
, а угол его осевого сечения равен 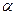 . Найти расстояние от вершины конуса до плоскости окружности, по которой сфера пересекает конус. Указать возможные значения для
. Найти расстояние от вершины конуса до плоскости окружности, по которой сфера пересекает конус. Указать возможные значения для 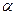 .
.
Решение. На последний вопрос, как видно из чертежа, ответ достаточно прост: необходимо, чтобы 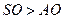 , откуда вытекает ограничение на величину угола
, откуда вытекает ограничение на величину угола 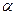 :
: 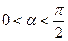 .
.
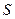
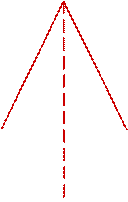

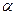


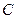


Вычислим радиус сферы: 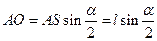 . Так как
. Так как  - равнобедренный, то
- равнобедренный, то 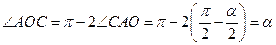 , поэтому
, поэтому 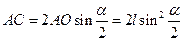 . Следовательно,
. Следовательно,
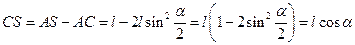 ,
,
и искомое расстояние 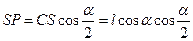 . #
. #
Решить задачи:
16) Высота конуса в 4 раза больше радиуса шара, вписанного в этот конус. Образующая конуса равна 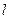 . Найти боковую поверхность конуса.
. Найти боковую поверхность конуса.
17) Отношение боковой поверхности усеченного конуса, описанного около шара, к сумме площадей его оснований равно 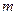 . Найти угол между образующей и плоскостью основания и допустимые значения
. Найти угол между образующей и плоскостью основания и допустимые значения 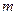 .
.
18) Центр сферы совпадает с центром основания кругового конуса, а ее радиус равен радиусу основания конуса. Длина образующей конуса равна 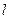 , а угол его осевого сечения равен
, а угол его осевого сечения равен 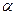 . Найти радиус окружности, по которой сфера пересекает конус. Указать возможные значения для
. Найти радиус окружности, по которой сфера пересекает конус. Указать возможные значения для 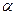 .
.
26 задание
1) Первая часть задания предполагает решение уравнений с двумя неизвестными.
Пример 1. Решить уравнение: 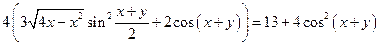 .
.
Решение. Заметим, что  , ибо в противном случае, получаем уравнение
, ибо в противном случае, получаем уравнение 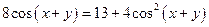 , которое не имеет решений, так
, которое не имеет решений, так 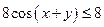 , а
, а 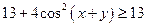 . Это замечание позволяет преобразовать заданное уравнение:
. Это замечание позволяет преобразовать заданное уравнение:
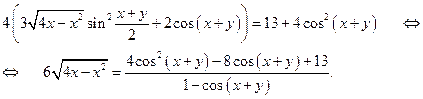
Найдем наибольшее значение функции  на отрезке
на отрезке 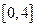 - области определения этой функции. Имеем:
- области определения этой функции. Имеем:  , поэтому
, поэтому 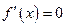 в точке
в точке 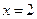 . Знаки производной показывают, что
. Знаки производной показывают, что  имеет в точке
имеет в точке 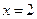 локальный максимум. Следовательно,
локальный максимум. Следовательно,  . Найдем теперь наименьшее значение функции
. Найдем теперь наименьшее значение функции  на промежутке
на промежутке  , где
, где 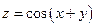 . Имеем:
. Имеем:
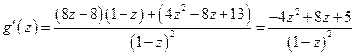 ,
,
поэтому
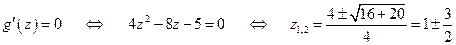 .
.
Условию 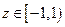 удовлетворяет только корень
удовлетворяет только корень 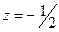 . Знаки производной показывают, что
. Знаки производной показывают, что  имеет в этой точке локальный минимум. Следовательно,
имеет в этой точке локальный минимум. Следовательно, 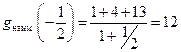 . Таким образом, для всех допустимых значений
. Таким образом, для всех допустимых значений  и
и 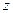 имеем:
имеем: 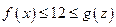 , откуда следует, что решение исходного уравнения возможно лишь в одном случае:
, откуда следует, что решение исходного уравнения возможно лишь в одном случае:
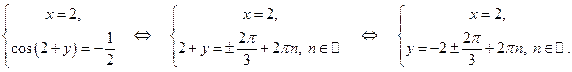 #
#
Решить уравнения:
1) 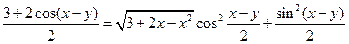 ;
;
2) 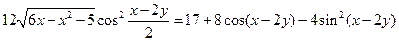 ;
;
3)  .
.
2) Во второй части задания предлагается решение задач, связанных с уравнениями и системами уравнений с параметрами.
Пример 2. При каких значениях параметра 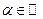 уравнение
уравнение 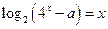 имеет два решения?
имеет два решения?
Решение. Имеем:
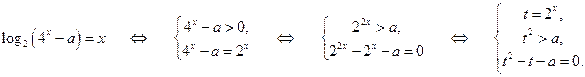
Так как функция 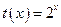 является строго возрастающей, т.е. биективной, а уравнение
является строго возрастающей, т.е. биективной, а уравнение  имеет корни
имеет корни 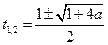 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда 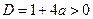 , т.е.
, т.е.  , и для меньшего корня
, и для меньшего корня 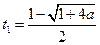 выполняется система неравенств:
выполняется система неравенств:
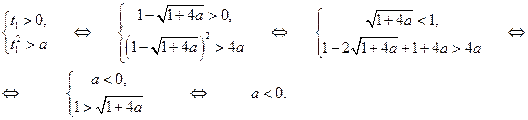
Таким образом, получаем ответ: 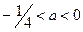 . #
. #
При каких значениях 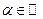 уравнение имеет единственное решение?
уравнение имеет единственное решение?
4) 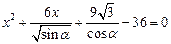 ; 5)
; 5)  ; 6)
; 6) 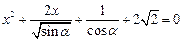 .
.
Для каких действительных чисел  уравнение имеет 2 действительных решения?
уравнение имеет 2 действительных решения?
7) 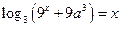 ; 8)
; 8) 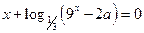 ; 9)
; 9)  .
.
Для каждого действительного числа  решить систему уравнений:
решить систему уравнений:
10)  11)
11) 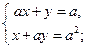 12)
12)  13)
13) 
14) 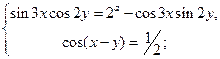 15)
15) 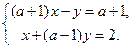
Для каких действительных чисел  система имеет два действительных решения?
система имеет два действительных решения?
16) 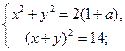 17)
17) 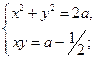 18)
18) 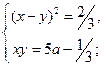 19)
19) 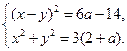
27 задание
1) В первой части задания приведены задачи на количество корней заданного уравнения с параметром.
Пример 1. Для каких действительных чисел  уравнение
уравнение 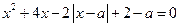 имеет 0, 1, 2, 3 или 4 действительных решений?
имеет 0, 1, 2, 3 или 4 действительных решений?
Решение. Перепишем уравнение в виде совокупности двух систем:
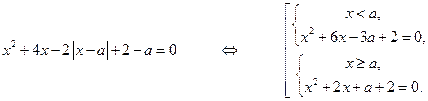
Пусть  - дискриминант верхнего уравнения в совокупности двух систем, а
- дискриминант верхнего уравнения в совокупности двух систем, а 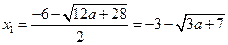 и
и 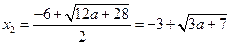 - его корни, и
- его корни, и 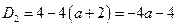 - дискриминант нижнего уравнения, а
- дискриминант нижнего уравнения, а  и
и 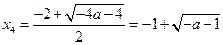 - его корни. Рассмотрим теперь случаи, когда верхняя система в совокупности (а затем и нижняя) имеет 0, 1 и 2 решения.
- его корни. Рассмотрим теперь случаи, когда верхняя система в совокупности (а затем и нижняя) имеет 0, 1 и 2 решения.
1) Первая система имеет 0 решений, т.е. не имеет решений:

2) Первая система имеет 1 решение:
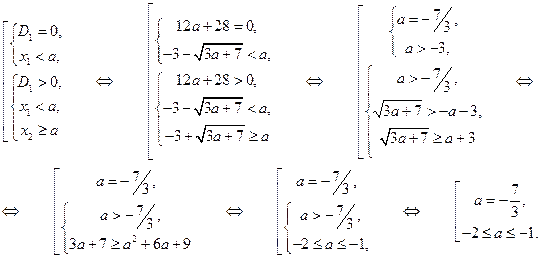
3) Первая система имеет 2 решения:
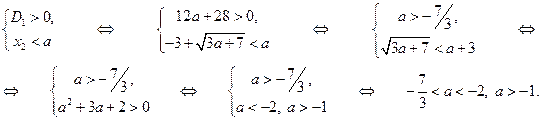
4) Вторая система имеет 0 решений:
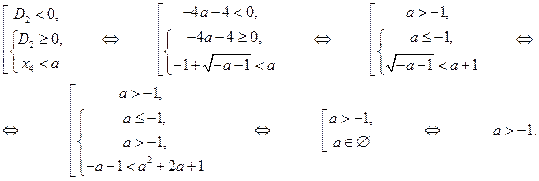
5) Вторая система имеет 1 решение:
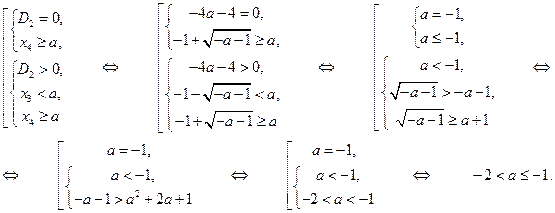
6) Вторая система имеет 2 решения:
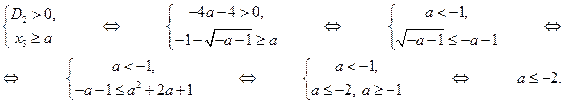
Теперь уже легко ответить на поставленные в условии задачи вопросы.
А) Заданное уравнение имеет 0 решений, когда первая и вторая системы имеют по 0 решений:

Б) Заданное уравнение имеет 1 решение, когда первая система имеет 1 решение, а вторая система имеет 0 решений, и наоборот:
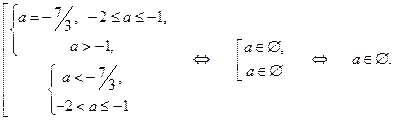
В) Заданное уравнение имеет 2 решения, когда первая и вторая системы имеют по 1 решению, или первая система имеет 2 решения, а вторая система имеет 0 решений, и наоборот:
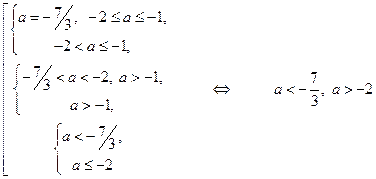 .
.
Г) Заданное уравнение имеет 3 решения, когда первая система имеет 2 решения, а вторая система имеет 1 решение, и наоборот:
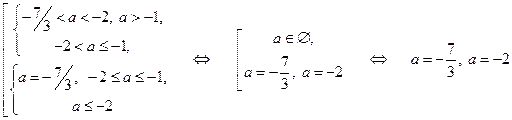 .
.
Д) Заданное уравнение имеет 4 решения, когда первая и вторая системы имеют по 2 решения:
 . #
. #
Для каких действительных чисел  уравнение имеет 0, 1, 2, 3, 4 решения?
уравнение имеет 0, 1, 2, 3, 4 решения?
1) 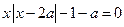 ; 2)
; 2) 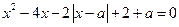 ; 3)
; 3) 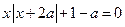 ;
;
4) 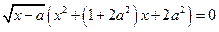 ; 5)
; 5)  .
.
Для каких действительных чисел  уравнение имеет на отрезке
уравнение имеет на отрезке 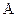 ровно
ровно 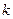 корней?
корней?
6) 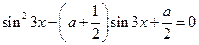 ,
, 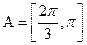 ,
,  ;
;
7) 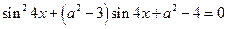 ,
, 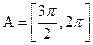 ,
,  .
.
2) Во второй части задания приведены задачи на расположение корней двух уравнений с одинаковым параметром.
Найти все  , при которых уравнения имеют по два различных действительных корня и между корнями одного уравнения содержится ровно один корень другого уравнения:
, при которых уравнения имеют по два различных действительных корня и между корнями одного уравнения содержится ровно один корень другого уравнения:
8) 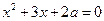 и
и 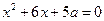 ; 9)
; 9) 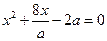 и
и 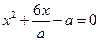 .
.
Найти все  , при которых уравнения имеют по два различных действительных корня и между корнями одного из уравнений нет ни одного корня другого уравнения:
, при которых уравнения имеют по два различных действительных корня и между корнями одного из уравнений нет ни одного корня другого уравнения:
10) 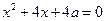 и
и 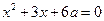 ; 11)
; 11)  и
и  .
.
12) Для каких действительных чисел  всякое решение неравенства
всякое решение неравенства 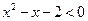 больше любого решения неравенства
больше любого решения неравенства 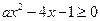 ?
?
13) Найти все действительные числа 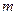 , при каждом из которых любое решение неравенства
, при каждом из которых любое решение неравенства 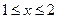 является решением неравенства
является решением неравенства 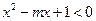 .
.
28 задание
Данное задание содержит задачи на неравенства с параметрами.
Пример 1. Для каждого действительного числа  решить неравенство:
решить неравенство: 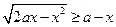
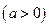 .
.
Решение. Найдем сначала область определения неравенства:
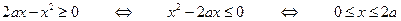 .
.
Далее, учитывая, что корни уравнения 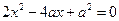 - это
- это 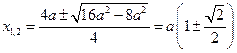 , имеем:
, имеем:
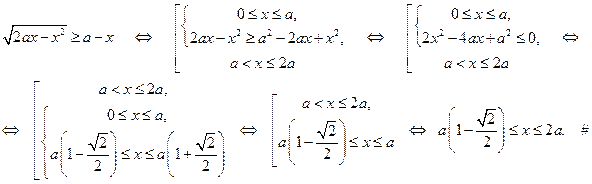
Для каждого действительного числа  решить неравенство:
решить неравенство:
1)  ; 2)
; 2)  ; 3)
; 3) 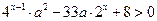 ;
;
4)  ; 5)
; 5)  ; 6)
; 6) 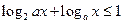 ;
;
7) 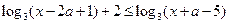 ; 8)
; 8) 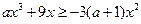 ; 9)
; 9) 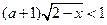 ;
;
10)  ; 11)
; 11) 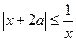 ; 12)
; 12)  ; 13)
; 13) 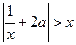 ; 14)
; 14) 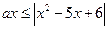 ;
;
15) 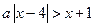 ; 16)
; 16) 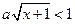 ; 17)
; 17)  ; 18)
; 18) 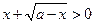
 .
.
29 задание
1) В первой части задания содержатся различные задачи на неравенства с параметрами.
Пример 1. Найти все действительные числа  , при каждом из которых неравенство
, при каждом из которых неравенство 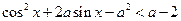 выполняется для всех действительных чисел
выполняется для всех действительных чисел  .
.
Решение. Преобразуем заданное неравенство:
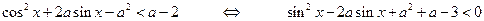
и положим 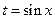 . Теперь исходная задача будет выглядеть следующим образом: найти все действительные числа
. Теперь исходная задача будет выглядеть следующим образом: найти все действительные числа  , при каждом из которых неравенство
, при каждом из которых неравенство  выполняется для всех
выполняется для всех 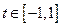 . Вычислим корни уравнения
. Вычислим корни уравнения  :
:
 .
.
Задача сводится теперь к выполнению включения: 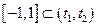 , где
, где 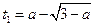 и
и  , т.е. к решению следующей системы неравенств:
, т.е. к решению следующей системы неравенств:
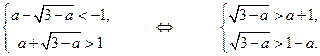
Решим по отдельности каждое из неравенств системы:

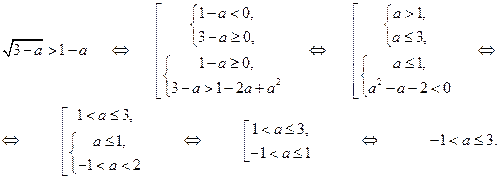
Таким образом, окончательно получаем:
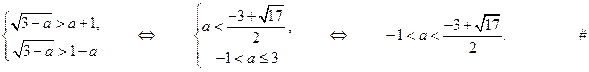
Для каких действительных чисел  (целых чисел
(целых чисел  ) неравенство верно для всех чисел
) неравенство верно для всех чисел  :
:
1) 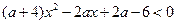 ; 2)
; 2) 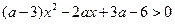 ; 3)
; 3) 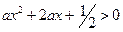 ; 4)
; 4) 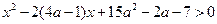 ; 5)
; 5) 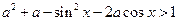 ;
;
6) 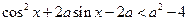 ; 7)
; 7) 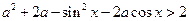 .
.
Найти все действительные числа  , при каждом из которых для всех
, при каждом из которых для всех  выполняется неравенство:
выполняется неравенство:
8) 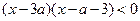 ,
, 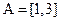 ; 9)
; 9)  ,
, 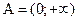 ;
;
10) 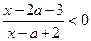 ,
, 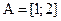 ; 11)
; 11) 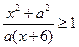 ,
, 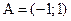 .
.
12) Найти все действительные числа 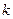 , при каждом из которых любое решение неравенства
, при каждом из которых любое решение неравенства 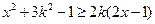 является решением неравенства
является решением неравенства 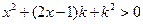 .
.
13) Найти все числа  , при каждом из которых любое действительное число
, при каждом из которых любое действительное число  является решением хотя бы одного из неравенств:
является решением хотя бы одного из неравенств: 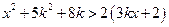 и
и 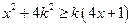 .
.
2) Во второй части задания содержатся задачи на сечения кубов и призм плоскостями.
Пример 2. В каком отношении делит объем куба 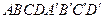 плоскость, проходящая через вершины
плоскость, проходящая через вершины  ,
, 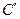 и точку
и точку 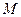 , расположенную на ребре
, расположенную на ребре  так, что
так, что 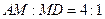 ? Найдите площадь и периметр полученного сечения (длина ребра куба равна
? Найдите площадь и периметр полученного сечения (длина ребра куба равна  ), а также расстояние от точки
), а также расстояние от точки 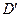 до секущей плоскости и угол между плоскостью нижнего основания и секущей плоскостью.
до секущей плоскости и угол между плоскостью нижнего основания и секущей плоскостью.
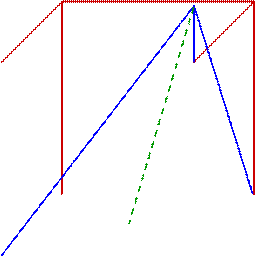
Решение. Пусть 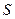 - точка пересечения продолжения ребра
- точка пересечения продолжения ребра  с прямой
с прямой  .
.
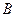
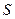
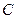





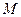
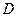







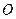


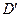
Искомое сечение – это равнобедренная трапеция 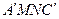 , образованная отсечением от равнобедренного
, образованная отсечением от равнобедренного 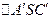 его вершины
его вершины 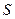 отрезком
отрезком 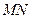 , параллельным
, параллельным 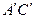 . Перейдем к необходимым вычислениям. Так как
. Перейдем к необходимым вычислениям. Так как  , то
, то 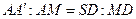 , откуда
, откуда 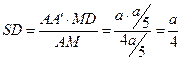 . Следовательно,
. Следовательно,  ,
, 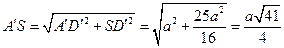 и
и 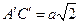 . Поскольку
. Поскольку 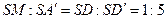 , то
, то  ,
,  и
и 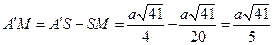 . Отсюда находим периметр сечения:
. Отсюда находим периметр сечения:
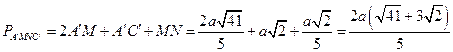 .
.
Далее заметим, что  является высотой
является высотой  (
( и
и  ), поэтому
), поэтому 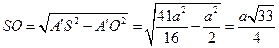 . Теперь легко найти площадь сечения:
. Теперь легко найти площадь сечения:
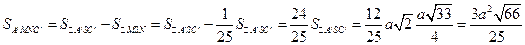 .
.
Далее вычислим объем пирамиды  :
: 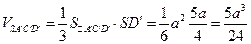 . С другой стороны, если
. С другой стороны, если 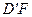 - перпендикуляр, опущенный из вершины куба
- перпендикуляр, опущенный из вершины куба 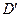 на плоскость
на плоскость 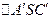 , то
, то 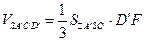 , поэтому можно найти расстояние от вершины
, поэтому можно найти расстояние от вершины 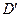 до секущей плоскости:
до секущей плоскости:
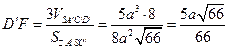 .
.
Теперь найдем объем передней части куба  :
:
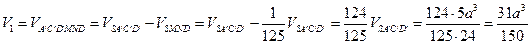
и объем задней части куба: 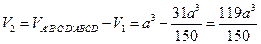 , откуда получаем отношение объмов двух частей, на которые делится куб секущей плоскостью:
, откуда получаем отношение объмов двух частей, на которые делится куб секущей плоскостью:
 .
.
Наконец, поскольку 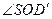 - это линейный угол двухгранного угла, образованного плоскостью нижнего основания куба и секущей плоскостью, а
- это линейный угол двухгранного угла, образованного плоскостью нижнего основания куба и секущей плоскостью, а 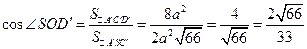 , то находим угол между плоскостью нижнего основания и секущей плоскостью:
, то находим угол между плоскостью нижнего основания и секущей плоскостью:
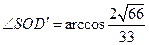 . #
. #
Решить задачи:
14) Дан куб  с ребром, равным
с ребром, равным  дм. На продолжении ребра
дм. На продолжении ребра 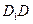 за точку
за точку 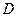 взята точка
взята точка 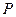 так, что
так, что 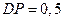 дм. Через точку
дм. Через точку 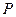 и середины ребер
и середины ребер 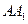 и
и  проведена плоскость. Найдите периметр и площадь полученного сечения, а также расстояние от точки
проведена плоскость. Найдите периметр и площадь полученного сечения, а также расстояние от точки 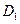 до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью. В каком отношении делит объем куба секущая плоскость?
до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью. В каком отношении делит объем куба секущая плоскость?
15) В каком отношении делит объем куба 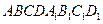 плоскость, проходящая через вершину
плоскость, проходящая через вершину 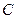 и середины ребер
и середины ребер 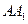 и
и 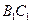 ? Найдите площадь и периметр полученного сечения (длина ребра куба равна
? Найдите площадь и периметр полученного сечения (длина ребра куба равна  ), а также расстояние от точки
), а также расстояние от точки 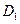 до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью.
до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью.
16) В каком отношении делит объем правильной треугольной призмы  плоскость, проходящая через вершину
плоскость, проходящая через вершину  и середины ребер
и середины ребер 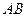 и
и  ? Найдите площадь и периметр сечения, если длины всех ребер призмы равны
? Найдите площадь и периметр сечения, если длины всех ребер призмы равны  , а также расстояние от точки
, а также расстояние от точки  до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью.
до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью.
17) Основание прямой призмы  - равносторонний треугольник
- равносторонний треугольник  со стороной
со стороной  дм. На продолжении ребра
дм. На продолжении ребра 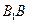 за точку
за точку  взята точка
взята точка 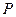 так, что
так, что  дм. Через точку
дм. Через точку 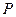 и середины ребер
и середины ребер 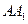 и
и  проведена плоскость. Найдите периметр и площадь полученного сечения, если
проведена плоскость. Найдите периметр и площадь полученного сечения, если 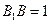 дм, а также расстояние от точки
дм, а также расстояние от точки 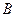 до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью. В каком отношении делит объем призмы секущая плоскость?
до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью. В каком отношении делит объем призмы секущая плоскость?
18) В прямоугольном параллелепипеде 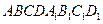 с ребрами
с ребрами  см и
см и 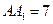 см через вершины
см через вершины  ,
,  и точку
и точку 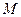 , лежащую на ребре
, лежащую на ребре 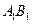 , проведена плоскость. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью?
, проведена плоскость. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью?
30 задание
1) В первой части задания содержатся различные задачи с параметрами.
Пример 1. Найти все числа  , для каждого из которых система
, для каждого из которых система 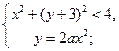 имеет действительные решения.
имеет действительные решения.
Решение. Если  , то
, то 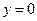 и неравенство системы предстает в виде
и неравенство системы предстает в виде  . Оно, а значит и сама система, действительных решений не имеет. Следовательно,
. Оно, а значит и сама система, действительных решений не имеет. Следовательно,  . Тогда
. Тогда 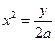 и неравенство можно переписать в виде:
и неравенство можно переписать в виде: 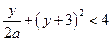 . Далее рассмотрим два случая.
. Далее рассмотрим два случая.
1) Пусть 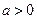 . Тогда
. Тогда
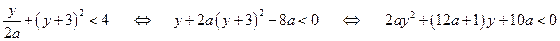 .
.
Найдем корни уравнения 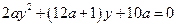 :
:
 .
.
Решением неравенства 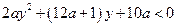 будет интервал
будет интервал
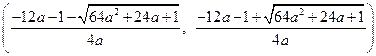
при условии, что дискриминант  . По условию задачи этот интервал должен содержать хотя бы одну точку
. По условию задачи этот интервал должен содержать хотя бы одну точку 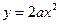 . Так как
. Так как 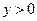 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда
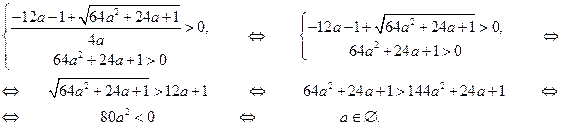
2) Пусть 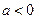 . Тогда
. Тогда
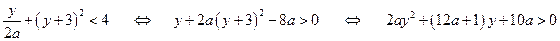 .
.
Решением неравенства 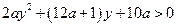 будет интервал
будет интервал

при условии, что дискриминант  . Так как
. Так как 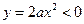 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда
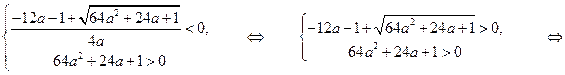
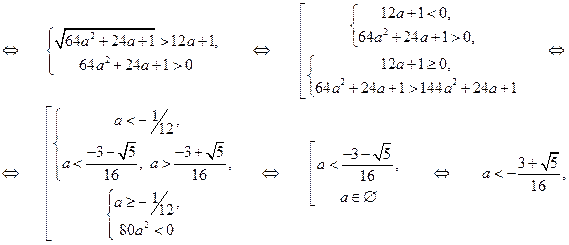
где  - корни уравнения
- корни уравнения 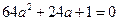 . #
. #
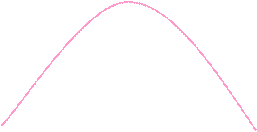
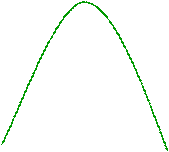
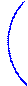
Замечание. Геометрический смысл задачи состоит в нахождении тех параметров  , при которых парабола
, при которых парабола 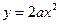 пересекает внутренность окружности
пересекает внутренность окружности 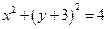 :
:


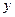
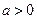




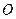

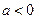
Пример 2. Найти множество всех пар 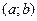 действительных чисел, для каждой из которых равенство
действительных чисел, для каждой из которых равенство 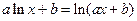 верно для всех положительных чисел
верно для всех положительных чисел  .
.
Решение. Подставим в равенство 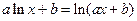 три значения:
три значения: 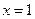 ,
, 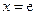 и
и 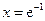 . Получим, соответственно, три равенства:
. Получим, соответственно, три равенства:
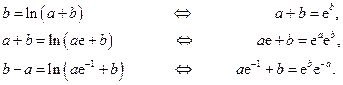
Составим систему уравнений относительно неизвестных  и
и  , возведя в квадрат первое равенство и перемножив второе и третье:
, возведя в квадрат первое равенство и перемножив второе и третье:

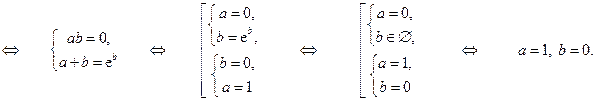
Итак, для того чтобы равенство 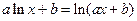 выполнялось для значений
выполнялось для значений 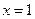 ,
, 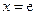 и
и 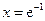 , необходимо, чтобы
, необходимо, чтобы  и
и 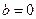 . Осталось лишь убедиться, что при этих значениях параметров
. Осталось лишь убедиться, что при этих значениях параметров  и
и  заданное равенство будет выполнено для всех
заданное равенство будет выполнено для всех  . Это действительно так, поскольку при
. Это действительно так, поскольку при  и
и 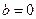 исходное равенство является тождеством:
исходное равенство является тождеством:  . #
. #
Найти все числа  , для каждого из которых система имеет действительные решения:
, для каждого из которых система имеет действительные решения:
1)  2)
2)  3)
3) 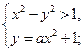 4)
4) 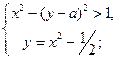 5)
5)  6)
6) 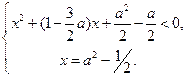 7)
7) 
Найти множество всех пар 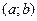 действительных чисел, для каждой из которых при всех
действительных чисел, для каждой из которых при всех  верно равенство:
верно равенство:
8) 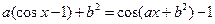 ; 9)
; 9) 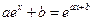 ; 10)
; 10) 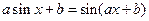 .
.
Доказать, что для всех действительных чисел  и
и  верно неравенство:
верно неравенство:
11) 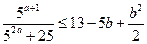 ; 12)
; 12)  ; 13)
; 13) 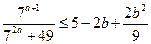 .
.
2) Во второй части задания содержатся задачи на пирамиды.
Пример 3. В правильной четырехугольной пирамиде 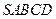 с вершиной
с вершиной 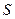 все ребра равны
все ребра равны  . Через вершину
. Через вершину 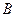 и середины ребер
и середины ребер 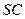 и
и  проведена плоскость. Найдите площадь и периметр сечения, отношение объемов рассекаемых плоскостью частей пирамиды, расстояние от вершины
проведена плоскость. Найдите площадь и периметр сечения, отношение объемов рассекаемых плоскостью частей пирамиды, расстояние от вершины 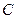 до секущей плоскости, а также угол между плоскостью основания и секущей плоскостью.
до секущей плоскости, а также угол между плоскостью основания и секущей плоскостью.
Решение. Пусть 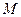 и
и  середины ребер
середины ребер  и
и 

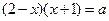 ; 12)
; 12) 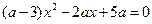 .
. корни уравнения
корни уравнения  будут неотрицательными (неположительными) действительными числами?
будут неотрицательными (неположительными) действительными числами?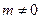 один из действительных корней уравнения
один из действительных корней уравнения  равен удвоенному действительному корню уравнения
равен удвоенному действительному корню уравнения 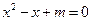 ?
? действительные корни уравнения
действительные корни уравнения 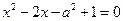 лежат между действительными корнями уравнения
лежат между действительными корнями уравнения 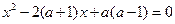 ?
? , а угол его осевого сечения равен
, а угол его осевого сечения равен 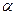 . Найти расстояние от вершины конуса до плоскости окружности, по которой сфера пересекает конус. Указать возможные значения для
. Найти расстояние от вершины конуса до плоскости окружности, по которой сфера пересекает конус. Указать возможные значения для 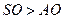 , откуда вытекает ограничение на величину угола
, откуда вытекает ограничение на величину угола 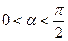 .
.





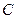
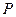
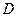




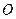

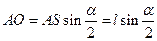 . Так как
. Так как  - равнобедренный, то
- равнобедренный, то 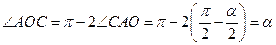 , поэтому
, поэтому 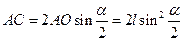 . Следовательно,
. Следовательно,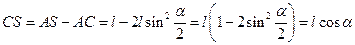 ,
,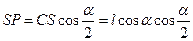 . #
. #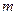 . Найти угол между образующей и плоскостью основания и допустимые значения
. Найти угол между образующей и плоскостью основания и допустимые значения 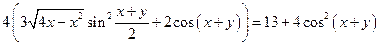 .
. , ибо в противном случае, получаем уравнение
, ибо в противном случае, получаем уравнение 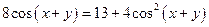 , которое не имеет решений, так
, которое не имеет решений, так 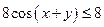 , а
, а 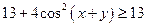 . Это замечание позволяет преобразовать заданное уравнение:
. Это замечание позволяет преобразовать заданное уравнение: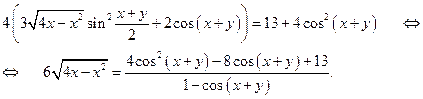
 на отрезке
на отрезке 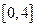 - области определения этой функции. Имеем:
- области определения этой функции. Имеем:  , поэтому
, поэтому 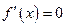 в точке
в точке 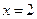 . Знаки производной показывают, что
. Знаки производной показывают, что  имеет в точке
имеет в точке  . Найдем теперь наименьшее значение функции
. Найдем теперь наименьшее значение функции 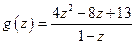 на промежутке
на промежутке  , где
, где 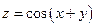 . Имеем:
. Имеем: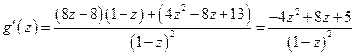 ,
,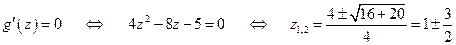 .
.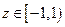 удовлетворяет только корень
удовлетворяет только корень 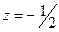 . Знаки производной показывают, что
. Знаки производной показывают, что  имеет в этой точке локальный минимум. Следовательно,
имеет в этой точке локальный минимум. Следовательно, 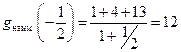 . Таким образом, для всех допустимых значений
. Таким образом, для всех допустимых значений  и
и  имеем:
имеем: 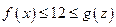 , откуда следует, что решение исходного уравнения возможно лишь в одном случае:
, откуда следует, что решение исходного уравнения возможно лишь в одном случае: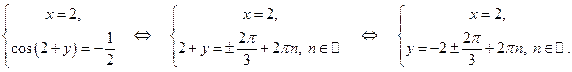 #
#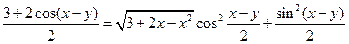 ;
;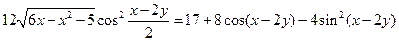 ;
; .
.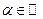 уравнение
уравнение 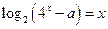 имеет два решения?
имеет два решения?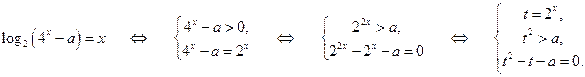
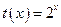 является строго возрастающей, т.е. биективной, а уравнение
является строго возрастающей, т.е. биективной, а уравнение  имеет корни
имеет корни 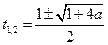 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда 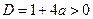 , т.е.
, т.е.  , и для меньшего корня
, и для меньшего корня 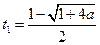 выполняется система неравенств:
выполняется система неравенств: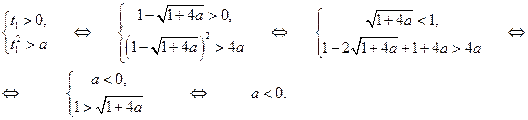
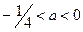 . #
. #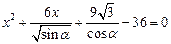 ; 5)
; 5)  ; 6)
; 6) 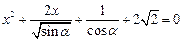 .
.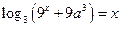 ; 8)
; 8) 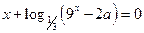 ; 9)
; 9)  .
. 11)
11) 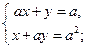 12)
12)  13)
13) 
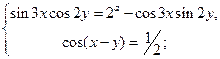 15)
15) 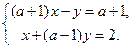
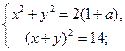 17)
17) 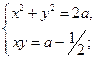 18)
18) 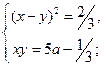 19)
19) 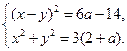
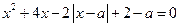 имеет 0, 1, 2, 3 или 4 действительных решений?
имеет 0, 1, 2, 3 или 4 действительных решений?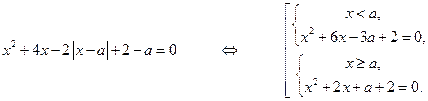
 - дискриминант верхнего уравнения в совокупности двух систем, а
- дискриминант верхнего уравнения в совокупности двух систем, а 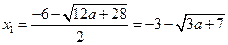 и
и 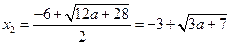 - его корни, и
- его корни, и 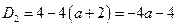 - дискриминант нижнего уравнения, а
- дискриминант нижнего уравнения, а  и
и 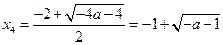 - его корни. Рассмотрим теперь случаи, когда верхняя система в совокупности (а затем и нижняя) имеет 0, 1 и 2 решения.
- его корни. Рассмотрим теперь случаи, когда верхняя система в совокупности (а затем и нижняя) имеет 0, 1 и 2 решения.
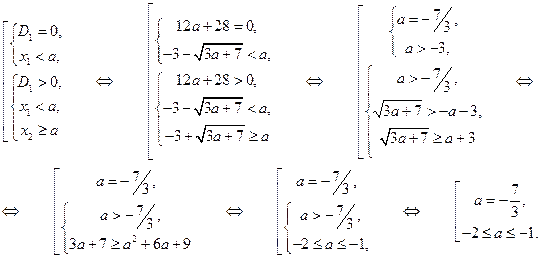
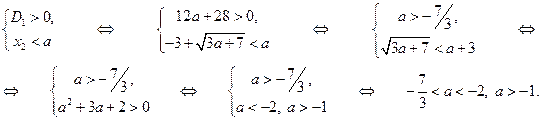
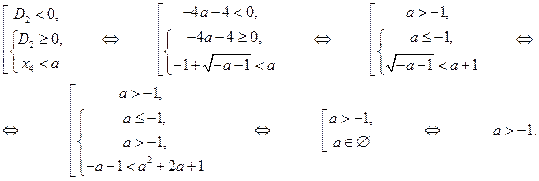
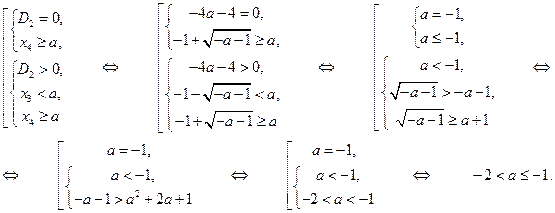
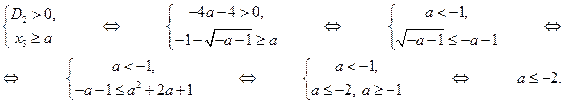

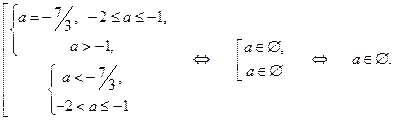
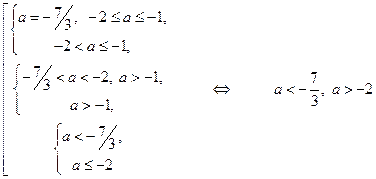 .
.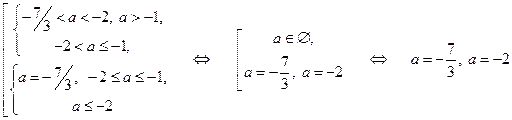 .
. . #
. #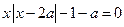 ; 2)
; 2) 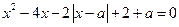 ; 3)
; 3) 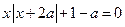 ;
;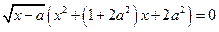 ; 5)
; 5)  .
. ровно
ровно  корней?
корней? 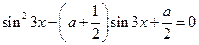 ,
, 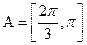 ,
,  ;
;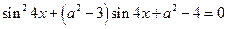 ,
, 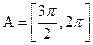 ,
,  .
. , при которых уравнения имеют по два различных действительных корня и между корнями одного уравнения содержится ровно один корень другого уравнения:
, при которых уравнения имеют по два различных действительных корня и между корнями одного уравнения содержится ровно один корень другого уравнения: 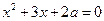 и
и 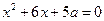 ; 9)
; 9) 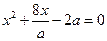 и
и 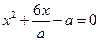 .
.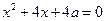 и
и 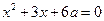 ; 11)
; 11)  и
и  .
.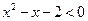 больше любого решения неравенства
больше любого решения неравенства 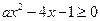 ?
?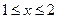 является решением неравенства
является решением неравенства 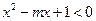 .
.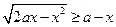
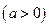 .
.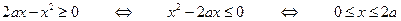 .
.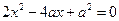 - это
- это 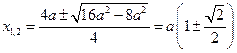 , имеем:
, имеем: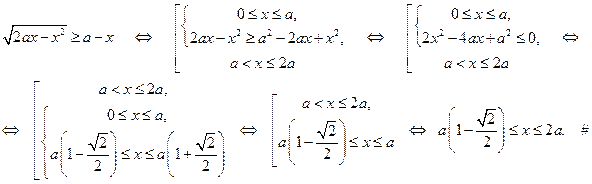
 ; 2)
; 2)  ; 3)
; 3) 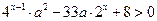 ;
; ; 5)
; 5)  ; 6)
; 6) 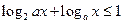 ;
;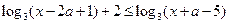 ; 8)
; 8) 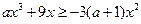 ; 9)
; 9) 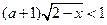 ;
; ; 11)
; 11) 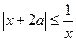 ; 12)
; 12)  ; 13)
; 13) 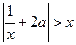 ; 14)
; 14) 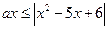 ;
;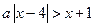 ; 16)
; 16) 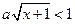 ; 17)
; 17)  ; 18)
; 18) 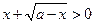
 .
.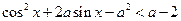 выполняется для всех действительных чисел
выполняется для всех действительных чисел 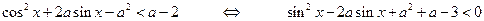
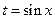 . Теперь исходная задача будет выглядеть следующим образом: найти все действительные числа
. Теперь исходная задача будет выглядеть следующим образом: найти все действительные числа  выполняется для всех
выполняется для всех 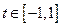 . Вычислим корни уравнения
. Вычислим корни уравнения  :
: .
.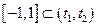 , где
, где 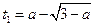 и
и  , т.е. к решению следующей системы неравенств:
, т.е. к решению следующей системы неравенств: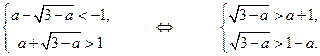

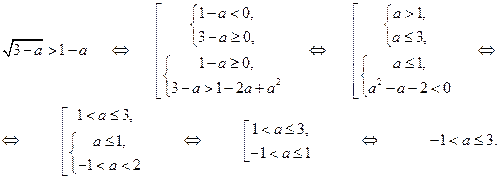
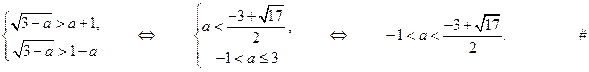
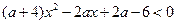 ; 2)
; 2) 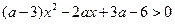 ; 3)
; 3) 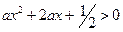 ; 4)
; 4) 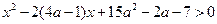 ; 5)
; 5) 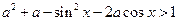 ;
;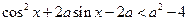 ; 7)
; 7) 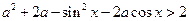 .
. выполняется неравенство:
выполняется неравенство: 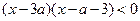 ,
, 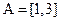 ; 9)
; 9)  ,
, 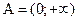 ;
;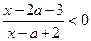 ,
, 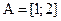 ; 11)
; 11) 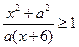 ,
, 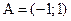 .
.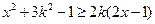 является решением неравенства
является решением неравенства 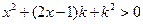 .
. , при каждом из которых любое действительное число
, при каждом из которых любое действительное число 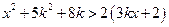 и
и 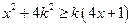 .
.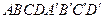 плоскость, проходящая через вершины
плоскость, проходящая через вершины  ,
, 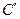 и точку
и точку 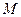 , расположенную на ребре
, расположенную на ребре  так, что
так, что 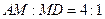 ? Найдите площадь и периметр полученного сечения (длина ребра куба равна
? Найдите площадь и периметр полученного сечения (длина ребра куба равна 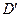 до секущей плоскости и угол между плоскостью нижнего основания и секущей плоскостью.
до секущей плоскости и угол между плоскостью нижнего основания и секущей плоскостью. с прямой
с прямой  .
.













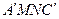 , образованная отсечением от равнобедренного
, образованная отсечением от равнобедренного 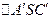 его вершины
его вершины 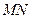 , параллельным
, параллельным 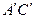 . Перейдем к необходимым вычислениям. Так как
. Перейдем к необходимым вычислениям. Так как  , то
, то 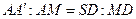 , откуда
, откуда 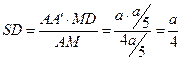 . Следовательно,
. Следовательно,  ,
, 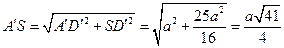 и
и 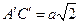 . Поскольку
. Поскольку 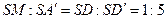 , то
, то  ,
,  и
и 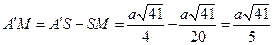 . Отсюда находим периметр сечения:
. Отсюда находим периметр сечения: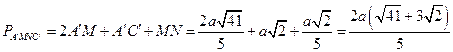 .
. является высотой
является высотой 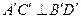 и
и  ), поэтому
), поэтому 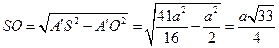 . Теперь легко найти площадь сечения:
. Теперь легко найти площадь сечения: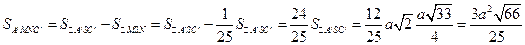 .
.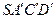 :
: 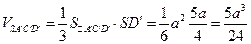 . С другой стороны, если
. С другой стороны, если  - перпендикуляр, опущенный из вершины куба
- перпендикуляр, опущенный из вершины куба 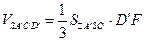 , поэтому можно найти расстояние от вершины
, поэтому можно найти расстояние от вершины 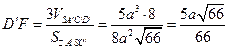 .
. :
: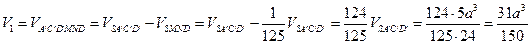
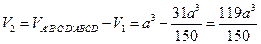 , откуда получаем отношение объмов двух частей, на которые делится куб секущей плоскостью:
, откуда получаем отношение объмов двух частей, на которые делится куб секущей плоскостью: .
.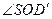 - это линейный угол двухгранного угла, образованного плоскостью нижнего основания куба и секущей плоскостью, а
- это линейный угол двухгранного угла, образованного плоскостью нижнего основания куба и секущей плоскостью, а 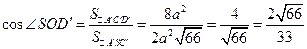 , то находим угол между плоскостью нижнего основания и секущей плоскостью:
, то находим угол между плоскостью нижнего основания и секущей плоскостью: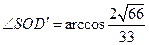 . #
. # с ребром, равным
с ребром, равным  дм. На продолжении ребра
дм. На продолжении ребра 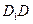 за точку
за точку 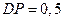 дм. Через точку
дм. Через точку 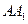 и
и  проведена плоскость. Найдите периметр и площадь полученного сечения, а также расстояние от точки
проведена плоскость. Найдите периметр и площадь полученного сечения, а также расстояние от точки 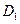 до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью. В каком отношении делит объем куба секущая плоскость?
до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью. В каком отношении делит объем куба секущая плоскость?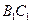 ? Найдите площадь и периметр полученного сечения (длина ребра куба равна
? Найдите площадь и периметр полученного сечения (длина ребра куба равна  плоскость, проходящая через вершину
плоскость, проходящая через вершину  и середины ребер
и середины ребер 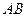 и
и  со стороной
со стороной 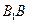 за точку
за точку  дм. Через точку
дм. Через точку 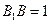 дм, а также расстояние от точки
дм, а также расстояние от точки  см и
см и 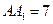 см через вершины
см через вершины  и точку
и точку 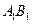 , проведена плоскость. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью?
, проведена плоскость. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью?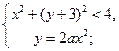 имеет действительные решения.
имеет действительные решения. , то
, то 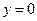 и неравенство системы предстает в виде
и неравенство системы предстает в виде  . Оно, а значит и сама система, действительных решений не имеет. Следовательно,
. Оно, а значит и сама система, действительных решений не имеет. Следовательно,  . Тогда
. Тогда 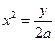 и неравенство можно переписать в виде:
и неравенство можно переписать в виде: 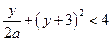 . Далее рассмотрим два случая.
. Далее рассмотрим два случая.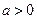 . Тогда
. Тогда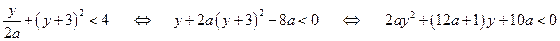 .
.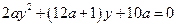 :
: .
.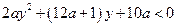 будет интервал
будет интервал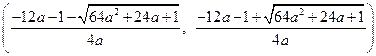
 . По условию задачи этот интервал должен содержать хотя бы одну точку
. По условию задачи этот интервал должен содержать хотя бы одну точку 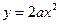 . Так как
. Так как 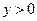 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда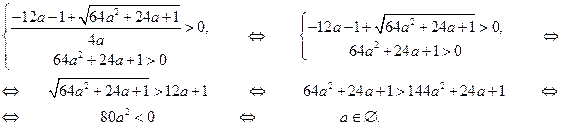
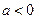 . Тогда
. Тогда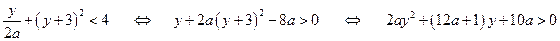 .
.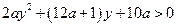 будет интервал
будет интервал
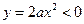 , то условие задачи будет выполнено в том и только том случае, когда
, то условие задачи будет выполнено в том и только том случае, когда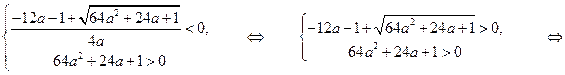
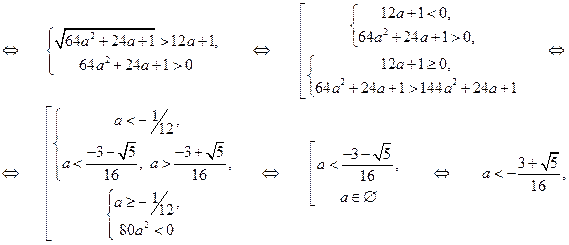
 - корни уравнения
- корни уравнения 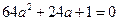 . #
. #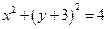 :
:

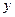







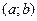 действительных чисел, для каждой из которых равенство
действительных чисел, для каждой из которых равенство 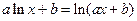 верно для всех положительных чисел
верно для всех положительных чисел 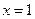 ,
, 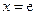 и
и 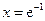 . Получим, соответственно, три равенства:
. Получим, соответственно, три равенства: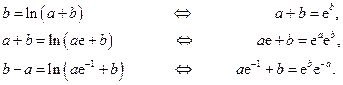
 , возведя в квадрат первое равенство и перемножив второе и третье:
, возведя в квадрат первое равенство и перемножив второе и третье:
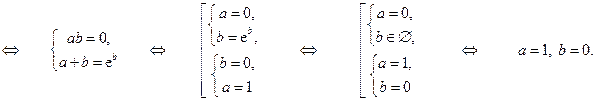
 и
и 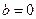 . Осталось лишь убедиться, что при этих значениях параметров
. Осталось лишь убедиться, что при этих значениях параметров  . Это действительно так, поскольку при
. Это действительно так, поскольку при  . #
. # 2)
2)  3)
3) 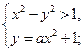 4)
4) 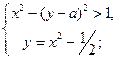 5)
5)  6)
6) 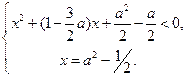 7)
7) 
 верно равенство:
верно равенство: 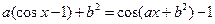 ; 9)
; 9) 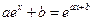 ; 10)
; 10) 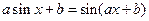 .
.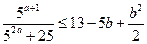 ; 12)
; 12)  ; 13)
; 13) 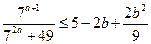 .
. с вершиной
с вершиной  и
и 


