Циклы двигателей внутреннего сгорания (ДВС)
Методические указания и методика расчета Двигатель внутреннего сгорания осуществляет преобразование теплоты, полученной при сгорании топлива, в механическую работу. В основу анализа действительных циклов поршневых двигателей внутреннего сгорания положены следующие три теоретических цикла: цикл с подводом теплоты при постоянном объеме (v = const) – близок по характеру протекания процессов к рабочему циклу карбюраторного двигателя; цикл с подводом теплоты при постоянном давлении (p =const) – близок к циклам в компрессорных дизелях; цикл с подводом теплоты при постоянных объеме и давлении (v = const и p = const) – обобщенный цикл по подводу теплоты, близок к циклам бескомпрессорных дизелей.Во всех трех циклах отвод теплоты осуществляется при постоянном объеме. При рассмотрении теоретических циклов принимаются следующие допущения: - циклы являются замкнутыми (обратимыми) и протекают при постоянном количестве одного и того же рабочего тела (идеального газа); - теплоемкость рабочего тела на протяжении всего цикла считается постоянной, не зависящей от температуры; - процесс сгорания топлива в цилиндре заменяется мгновенным условным подводом теплоты, а выброс отработанных газов – мгновенным условным отводом теплоты; - сжатие и расширение рабочего тела осуществляется в адиабатном процессе, т.е. без теплообмена с окружающей (внешней) средой.
Методика расчета обобщенного цикла с последовательным подводом теплоты при постоянном объеме и давлении. Введем следующие обозначения безразмерных параметров циклов Как было отмечено, совершенство термодинамического цикла оценивается его термическим КПД. Для рассматриваемого цикла:
Подставляя q1 и q2 в формулу
Воспользовавшись основными термодинамическими закономерностя-ми, выразим температуру в характерных точках через начальную температуру Тa и безразмерные параметры цикла. Запишем уравнения состояния для рабочего тела в точках а и с:
Разделив первое уравнение на второе, получим
откуда Из уравнения адиабаты имеем Тогда температура в точке с Записав уравнения состояния газа для точек
Так как
тогда
Из уравнений состояния газа для точек
Рисунок 3.1- Цикл ДВС с подводом теплоты при постоянном объёме и давлении на диаграммах p, v и T, s. Так как Наконец, из уравнений состояния газа в точках z и b из уравнения адиабаты имеем
Значит,
Подставляя значения температур в характерных точках в выражение для КПД цикла, получим
Приведем эту формулу к виду
с учетом того, что
Термический КПД обобщенного цикла увеличивается при увеличении степени сжатия
Работа теоретического цикла определяется по формуле Поскольку
и
то
Так как
Наиболее эффективным способом увеличения среднего давления является повышение начального давления ра. Циклы с подводом теплоты при р= const или υ = const являются частными случаями рассмотренного обобщенного цикла. При Следует обратить особое внимание, что в данных циклах отвод теплоты осуществляется в изохорном процессе. При этом параметры газа в конце процесса расширения значительно превышают параметры окружающей среды. Термодинамический цикл с продолженным расширением может быть осуществлен в комплексной установке двигателя и турбонагнетателя, состоящего из газовой турбины и компрессора (рисунок 3.2, рисунок 3.3). В газовой турбине происходит дальнейшее расширение газов, а полученная при этом энергия расходуется на привод нагнетателя для наддува двигателя. Циклы установки с продолженным расширением, переменным и постоянным давлением газов перед турбиной представлены соответственно на рисунке 3.2 и на рисунке 3.3. Термический КПД циклов соответственно
где bf - продолженное расширение газа на лопатках турбины; f0 – отвод теплоты при р = const; 0а – адиабатное сжатие воздуха в нагнетателе;
Из сравнения выражений для КПД обобщенного цикла и цикла с продолженным расширением газов видно, что КПД последнего выше. Это относится также к циклу с продолженным расширением, когда давление перед турбиной поддерживается постоянным, и кинетическая энергия отработавших газов не используется на лопатках турбины (рисунок 3.3.)
|

 - степень предварительного расширения;
- степень предварительного расширения;  - степень повышения давления;
- степень повышения давления; 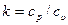 - показатель адиабаты.
- показатель адиабаты.
 .
. , получим
, получим
 ,
, 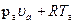 .
. ,
,  ,
, .
. и
и  .
.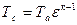 .
. и с и разделив почленно первое на второе, получим:
и с и разделив почленно первое на второе, получим: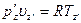 ;
;  .
. и
и  , то
, то  ;
; ;
; ;
; .
. и
и  ;
;  ;
; 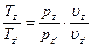 .
.
 ;
;  , то
, то 
 ;
;  ;
; 
 .
.
 , откуда
, откуда .
. .
.
 и
и  .
. , степени повышения давления
, степени повышения давления  , показателя адиабаты к и уменьшается при увеличении степени предварительного расширения
, показателя адиабаты к и уменьшается при увеличении степени предварительного расширения  . Однако чем больше
. Однако чем больше  .
. . Отношение работы цикла к рабочему объему цилиндра (удельная работа) характеризует среднее давление цикла
. Отношение работы цикла к рабочему объему цилиндра (удельная работа) характеризует среднее давление цикла  .
.
 ,
,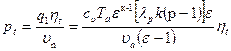 .
.
 , выражение для среднего давления газа в обобщенном цикле будет иметь вид
, выражение для среднего давления газа в обобщенном цикле будет иметь вид
 обобщенный цикл представляет собой цикл с изобарным подводом теплоты, а при ρ =1 – цикл с изохорным подводом теплоты.
обобщенный цикл представляет собой цикл с изобарным подводом теплоты, а при ρ =1 – цикл с изохорным подводом теплоты. ;
; ,
, - общая степень сжатия.
- общая степень сжатия.






