Методические указания к расчету холодильной установки
Определяются следующие характеристики установки. 1. Параметры хладагента (р, T, h) в характерных точках цикла и удельный объем 2. Удельная массовая и объемная холодопроизводительности q0 и qu по формулам соответственно:
3. Масса хладагента, циркулирующего в системе:
4. Действительный объем, описанный поршнем (для поршневых компрессоров):
5. Теоретическая работа сжатия в компрессоре
6. Расход охлаждающей воды в компрессоре
удельная теплота парообразования
7. Удельное количество теплоты, отдаваемой хладагентом в конденсаторе
8. Количество рассола, циркулирующего в холодильных камерах
9. Теоретическая мощность компрессора
10.Индикаторная мощность
11.Эффективная мощность
12.Мощность электродвигателя для привода компрессора
13.Теоретический холодильный коэффициент
14.Действительный холодильный коэффициент
15.Для подбора компрессора необходимо заданную холодопроизводительность пересчитать на стандартную. Для стандартных условий: t0=-150C; tk=300C; tn=250C.
По полученной холодопроизводительности для стандартных условий из таблиц подбирают тип компрессора.
5. Типовые задачи термодинамики с решениями
5.1.Расчет цикла ДВС. Для идеального цикла поршневого двигателя внутреннего сгорания со смешанным подводом тепла, определить параметры рабочего тела в характерных точках, термический КПД, количество отведенной теплоты, полезную работу и степень заполнения цикла, если начальные параметры рабочего тела
Параметры точки 1:
Параметры точки 2: т.к. степень сжатия Параметры точки 3: из соотношения параметров в изохорном процессе получаем
Параметры точки 4: из соотношения параметров в изобарном процессе получаем,
Параметры точки 5:
Температура в конце адиабатного расширения Определим удельное количество подведенной теплоты
Определим удельное количество отведенной теплоты
Полезная удельная работа
Полезно используемое удельное количество теплоты
Термический КПД цикла Для расчета степени заполнения цикла воспользуемся следующей формулой:
где Работа для цикла Карно находится по формуле:
Изменение удельное энтропий воздуха найдем по следующим формулам: где Процесс
Вычисляем удельный объем воздуха в точке
Процесс
Вычисляем удельный объем воздуха в точке
Вычисляем изменение удельных энтропий воздуха:
Подставляем полученные значения изменения удельных энтропий в выражениях для
Полученные значения подведенного и отведенного удельного тепла подставляем в выражение работы
Рассчитываем степень заполнения цикла
Ответ: параметры рабочего тела в характерных точках:
Точка 1: Точка 2: Точка 3: Точка 4: Точка 5:
5.2. Расчет цикла ГТУ. Газотурбинная установка работает с изобарным подводом теплоты. Параметры окружающей среды, поступающей на компрессор: температура T 1=15 °С; давление P 1=0, 098 МПа. Параметры рабочего тела за газовой турбиной: температура T 4д =550° С; расход G =127 кг/с. Степень повышения давления β =19. Мощность на валу ГТУ Nгту=47 МВт. Рабочие тело – воздух. Сжатие и расширение рабочего тела происходит необратимо. Относительный внутренний КПД компрессора Определить 1) Количество теплоты подводимое и отводимое от ГТУ 2) Электрический КПД газотурбинной установки; 3) Расход топлива 4) Термодинамические параметры (температура; давление; удельный объем) всех точек цикла. Решение Цикл данной газотурбинной установки изображен на рис. 1. 1. Расчет количества теплоты, отводимого от ГТУ (q 2)
Где ср=1, 088 кДж/(кг·°С) из [1]. 2. Расчет количества теплоты, подводимого к ГТУ (q 1)
3. Определим расход топлива на ГТУ
4. Определим электрический КПД установки
(6)
5. Определим термодинамические параметры всех точек цикла а) Точка 1 p 1=0, 098 МПа; Т 1=288 К
Где R=287 кДж/(кг·К) – газовая постоянная для воздуха
б)Точка 2
(12)
в) Точка 2д
в) Точка 3
где ср=1, 160 кДж/(кг·°С) из [1]. б) Точка 4д p 4д= р 4=0, 098 МПа; Т 4д=823 К
5.3. Расчет цикла паротурбинной установки. В паротурбинной установке с начальными параметрами пара р1=14 МПа, t1 = 550 °C и давлением в конденсаторе р2 = 0, 018 МПа был введен промежуточный перегрев пара при давлении р’=19 бардо температуры t’=450° C. Найти η tцикла с промежуточным перегревом и сравнить его с η tцикла Ренкина до введения промежуточного перегрева пара, а также определить КПД цикла и удельный расход пара, если для подогрева питательной воды из турбины отбирался пар до введения промежуточного перегрева при давлении р отб = 3 МПа. Оценить влияние промежуточного перегрева на конечную степень сухости пара в процессе расширения, а также эффективность использования регенеративного подогрева в цикле с отбором пара. Процессы расширения в турбине изобразить в h-s – диаграмме. Решение: КПД цикла со вторичным перегревом пара можно определить по формуле:
По h-s – диаграмме для начальных параметров р 1 = 14 МПа и t 1 = 550 ° С находим энтальпию:
Процесс расширения адиабатный, поэтому опускаемся вертикально вниз до пересечения с изобарой р’ = 19 бар и находим энтальпию в точке a:
Далее по изобаре р’ = 19 бар поднимаемся до пересечения с изотермой t’= 450 °C и получаем энтальпию в точке b:
Затем по адиабате опускаемся до пересечения с изобарой р2 = 18 кПа и находим энтальпию в точке 2:
Энтальпия Тогда термический КПД цикла Ренкина с промежуточным перегревом:
Конечная степень сухости:
где
Для цикла Ренкина до введения промежуточного перегрева пара:
где h2’ находим, опускаясь по адиабате из точки 1 до пересечения с изобарой p2=18 кПа. Получаем h2’ =2149 кДж/кг. Тогда:
Степень сухости:
Рисунок 5.1- Фрагмент h, s- диаграммы
Термический КПД паросиловой установки с регенеративным теплообменником будет определяться следующим образом:
Значения энтальпий
Затем, используя h-s – диаграмму, опускаясь из точки 1 до пересечения с изобарой ротб, находим энтальпию в точке 21: Количество отобранного пара:
Рассчитываем термический КПД:
Удельный расход пара в регенеративном цикле:
Примечание. Промежуточный перегрев позволяет повысить степень сухости пара, что приводит к увеличению КПД паротурбинной установки и повышению долговечности лопаток турбины, так как чем больше степень сухости пара, тем меньше коррозии на лопатках турбины. Регенеративный цикл является эффективным способом повышения КПД паротурбинных установок. 5.4. Расчеты сужающегося сопла и сопла Лаваля. Определить теоретическую скорость истечения водяного пара из сужающегося сопла (ω '2) и из сопла Лаваля (ω ''2) в среду с давлением p2=0, 1 МПа, если абсолютное давление пара на входе в сопло р 1 = 3 МПа, температура пара на входе в сопло t 1 = 480 ° С. Сделать выводы по эффективности использования сопла Лаваля. Также определить действительную скорость истечения пара из сопла Лаваля (ω ''2д) и определить его основные размеры (при действительном истечении), если расход пара M = 18 кг/с, скоростной коэффициент сопла 0, 95, а угол конусности расширяющейся части сопла 10°. Действительный процесс изобразить в масштабе. Задачу решить с помощью таблиц водяного пара и/или h-s – диаграммы. Решение: Определим режим истечения пара из сопла. Так как отношение
Из соотношения
По h-s – диаграмме для начальных параметров р 1 = 3 МПа и t 1 = 480 ° С находим энтальпию в точке 1:
Затем опускаемся по адиабате до пересечения с изобарой
Получаем скорость истечения из сужающегося сопла:
Скорость
Чтобы найти энтальпию
Значит:
Сопло Лаваля позволяет повысить скорость истечения пара в 2, 05 раза. Теперь рассчитаем сопло Лаваля при действительном истечении пара. Действительную скорость истечения на выходе из сопла Лаваля можем найти по формуле:
Коэффициент потери энергии в сопле:
Тогда, т.к.
Зная энтальпию Действительную скорость истечения в критическом сечении сопла Лаваля можем найти по формуле:
Минимальное сечение можем найти по формуле:
где
Теперь можем определить диаметр, он равен:
Тогда выходное сечение:
а диаметр:
Длина расширяющейся части сопла Лаваля:
Рисунок 5.2- Фрагмент h, s- диаграммы Примечание. Сопло Лаваля позволяет значительно увеличить скорость истечения пара по сравнению с сужающимся соплом, даже при учете реального режима истечения пара.
Литература
|

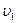 всасываемых паров (из T, s-диаграммы хладагента).
всасываемых паров (из T, s-диаграммы хладагента).









 где
где  - индикаторный КПД, равный
- индикаторный КПД, равный  коэффициент подогрева
коэффициент подогрева 
 - для аммиачных вертикальных простого действия;
- для аммиачных вертикальных простого действия; - для фреоновых вертикальных простого действия.
- для фреоновых вертикальных простого действия. где
где  - механический КПД,
- механический КПД,  где
где  - электрический КПД,
- электрический КПД, 

 где
где  - коэффициент подачи, равный
- коэффициент подачи, равный  ,
, - объемный коэффициент компрессора, равный
- объемный коэффициент компрессора, равный  ,
,  - отношение объема вредного пространства к действительному объему, в расчете принять С=5%,
- отношение объема вредного пространства к действительному объему, в расчете принять С=5%, - коэффициент неплотности, принять
- коэффициент неплотности, принять 
 и
и  , степень сжатия
, степень сжатия  , степень повышение давления
, степень повышение давления  и степень предварительного расширения. Данный цикл ДВС изображен в р, v- и Т, s- координатах на рис. 3.1, где ддля характерных точек цикла приняты буквенные обозначения, соответственно т.1 (а), т.2 (с), т.3 (
и степень предварительного расширения. Данный цикл ДВС изображен в р, v- и Т, s- координатах на рис. 3.1, где ддля характерных точек цикла приняты буквенные обозначения, соответственно т.1 (а), т.2 (с), т.3 ( ), т.4 (z), т.5 (в).
), т.4 (z), т.5 (в). =0, 855 м3/кг, р1=0, 1 МПа, t1=250C, где
=0, 855 м3/кг, р1=0, 1 МПа, t1=250C, где  .
. то
то  , температура в конце адиабатного сжатия
, температура в конце адиабатного сжатия  , давление в конце адиабатного сжатия
, давление в конце адиабатного сжатия  .
. .
.
 , давление в конце адиабатного расширения
, давление в конце адиабатного расширения .
. .
.
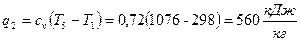 .
. :
:
 .
.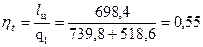 .
. ,
, - работа цикла поршневого двигателя;
- работа цикла поршневого двигателя;  - работа цикла Карно, заключенного в интервале максимальных температур цикла поршневого двигателя.
- работа цикла Карно, заключенного в интервале максимальных температур цикла поршневого двигателя. , где
, где  и
и  соответственно количество подтвержденного и отведенного удельного тепла в цикле Карно, которое находится из следующих уравнений:
соответственно количество подтвержденного и отведенного удельного тепла в цикле Карно, которое находится из следующих уравнений: и
и  , где
, где  и
и  - соответственно изменение удельных энтропий воздуха в процессах
- соответственно изменение удельных энтропий воздуха в процессах  -4 и
-4 и  .
. и
и 
 ,
,  - удельные объемы воздуха соответственно в точках
- удельные объемы воздуха соответственно в точках 
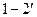 является адиабатным, поэтому для него справедливо следующее соотношение:
является адиабатным, поэтому для него справедливо следующее соотношение: ; т.е.
; т.е.  Т.к. процесс
Т.к. процесс  .
.
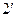 :
:
 тоже является адиабатным, поэтому имеем:
тоже является адиабатным, поэтому имеем: т.е.
т.е.  Т.к. процесс
Т.к. процесс  .
.


 и
и  :
:

 :
:
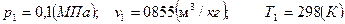 ;
; ;
; ;
; ;
; .
.
 , турбины
, турбины  . КПД генератора 97, 5%; редукторной передачи 99%. Низшая теплотворная способность топлива – 33, 4 МДж/м3.
. КПД генератора 97, 5%; редукторной передачи 99%. Низшая теплотворная способность топлива – 33, 4 МДж/м3. (1)
(1) , МВт (2)
, МВт (2) , кДж/кг (3)
, кДж/кг (3)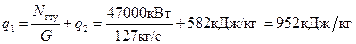 (4)
(4) (5)
(5)
 - уравнение Менделеева – Клапейрона (7)
- уравнение Менделеева – Клапейрона (7) м3/кг (8)
м3/кг (8) (9)
(9) - уравнение Клапейрона (10)
- уравнение Клапейрона (10) (11)
(11)

 (13)
(13)
 (14)
(14) (15)
(15) м3/кг.
м3/кг. ,
, кДж/кг.
кДж/кг. кДж/кг.
кДж/кг. кДж/кг.
кДж/кг. кДж/кг.
кДж/кг. кДж/кг (по таблицам воды и водяного пара).
кДж/кг (по таблицам воды и водяного пара). .
. ,
, кДж/кг. Получаем:
кДж/кг. Получаем: .
. ,
, .
. .
.

 и
и  кДж/кг берем из решения задачи выше:
кДж/кг берем из решения задачи выше: кДж/кг.
кДж/кг.
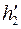 и
и  определяются по таблицам воды и водяного пара:
определяются по таблицам воды и водяного пара: кДж/кг.
кДж/кг.


 кг/(кВт·ч).
кг/(кВт·ч). , то скорость истечения из сужающегося сопла можно определить по формуле:
, то скорость истечения из сужающегося сопла можно определить по формуле: .
.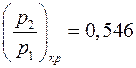 находим давление:
находим давление: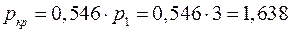 МПа.
МПа. кДж/кг.
кДж/кг. МПа и определяем энтальпию:
МПа и определяем энтальпию: кДж/кг.
кДж/кг. м/c.
м/c.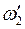 равна скорости истечения в минимальном сечении сопла Лаваля. Скорость истечения на выходе из сопла Лаваля определяется по формуле:
равна скорости истечения в минимальном сечении сопла Лаваля. Скорость истечения на выходе из сопла Лаваля определяется по формуле: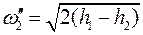 , где
, где  - энтальпия пара в точке 2.
- энтальпия пара в точке 2. кДж/кг.
кДж/кг. м/с.
м/с.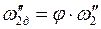 , где φ – скоростной коэффициент сопла Лаваля.
, где φ – скоростной коэффициент сопла Лаваля. м/с.
м/с.
 , то энтальпия пара в конце действительного процесса истечения
, то энтальпия пара в конце действительного процесса истечения  равна:
равна: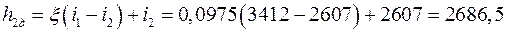 кДж/кг.
кДж/кг. м3/ кг.
м3/ кг. м/с.
м/с. ,
, – удельный объем пара при давлении
– удельный объем пара при давлении  м3/ кг.
м3/ кг. см2.
см2. см.
см. см2,
см2, см.
см.
 см.
см.


