Задачі обробки одновимірних та двовимірних масивів
В системі Mathcad використовуються масиви двох типів: одновимірні (вектори) та двовимірні (матриці). Порядковий номер елемента одновимірного масиву називається індексом. Індекси починаються з нуля або одиниці в залежності від значення системної змінної ORIGIN. Вектори і матриці можна задавати різними способами: 1. за допомогою команди Вставка ®Матрица; 2. за допомогою комбінації клавіш Ctrl+M; 3. клацанням на кнопці Щоб звернутися до окремих елементів вектора, використовують оператор нижнього індексу
Обробка елементів двовимірного масиву здійснюється так само, як і обробка елементів одновимірного масиву. Єдина відмінність – це те, що необхідно використовувати вкладені цикли: один цикл зовнішній для переміщення між рядками, а другий внутрішній, для переходу між елементами рядка. Над двовимірними масивами визначені функції: cols, rows, min, max. Приклад 1. Вивести на екран індекс нульового елементу масиву А=(5, 9, -4, 0, 2). Результат виконання завдання матиме такий вигляд:
Приклад 2. Знайти добуток елементів массиву Результат виконання завдання матиме такий вигляд:
Приклад 3. В матриці А= Результат виконання завдання матиме такий вид:
Приклад 4. Скласти програму знаходження суми двох двовимірних масивів. Результат записати в третій масив. Результат виконання завдання матиме такий вигляд:
Приклад 5. Обчислити добуток елементів головної діагоналі матриці Результат виконання завдання матиме такий вигляд:
Приклад 10. Обчислити добуток елементів побічної діагоналі матриці Результат виконання завдання матиме такий вигляд:
ОСНОВИ РОБОТИ В СИСТЕМІ MATLAB 1 Основні теоретичні відомості
Запуск системи MATLAB здійснюється натисканням лівої кнопки миші на піктограмі в полі робочого столу Windows або виконанням послідовності наступних команд:
Для виконання будь-яких команд та виразів їх потрібно надрукувати за допомогою клавіатури, відредагувати у командному рядку, якщо це необхідно і завершити введення натисканням клавіші Enter. Для уточнення версії системи варто вивести вікно (див. рис. 6.1) з інформацією про систему (команда About MATLAB у меню Help). Усі можливості системи, які описані у даному виданні, відносяться до розширеної і доповненої версії MATLAB 6.1 з пакетом розширення Simulink 4.1.
|

 панелі Матрица.
панелі Матрица. . Для роботи з масивами використовують вбудовані в Mathcad функції, які викликаються командами Вставка®Функция®Вектор и матрица. Нехай задано масив A=(3, 12, 0, 4, -1).
. Для роботи з масивами використовують вбудовані в Mathcad функції, які викликаються командами Вставка®Функция®Вектор и матрица. Нехай задано масив A=(3, 12, 0, 4, -1).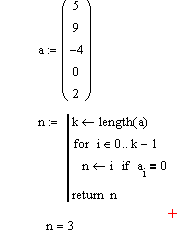
 =(-8, 5, 1, 4, 3).
=(-8, 5, 1, 4, 3).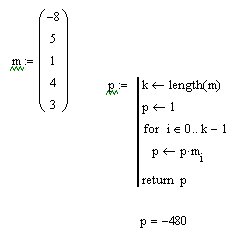
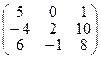 обчислити суму значень елементів кожного рядка.
обчислити суму значень елементів кожного рядка.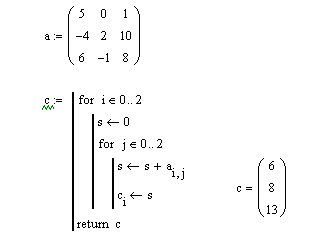




 ПУСК ® ПРОГРАМИ ® MATLAB (рис. 6.1).
ПУСК ® ПРОГРАМИ ® MATLAB (рис. 6.1). Після виконання однієї з описаних вище операцій розкривається вікно системи MATLAB з активним робочим простором (Work-space), зображене на (рис. 6.2). Воно має звичайні для до-датків WINDOWS органи керування для розширення, переміщення та закриття. Система відразу ж готова до роботи в режимі прямих обчислень, тобто, без попередньої підготовки програми. Це перетворює MATLAB у надзвичайно могутній калькулятор, який здатний робити не тільки звичайні обчислення, але й операції з векторами і матрицями, комплексними числами, рядами та поліномами. Можна майже миттєво задати і вивести графіки різних функцій, від простої синусоїди до складної тривимірної фігури. Цей процес супроводжується звуковою анімацією. Робота із системою в режимі прямих обчислень носить діалоговий характер.
Після виконання однієї з описаних вище операцій розкривається вікно системи MATLAB з активним робочим простором (Work-space), зображене на (рис. 6.2). Воно має звичайні для до-датків WINDOWS органи керування для розширення, переміщення та закриття. Система відразу ж готова до роботи в режимі прямих обчислень, тобто, без попередньої підготовки програми. Це перетворює MATLAB у надзвичайно могутній калькулятор, який здатний робити не тільки звичайні обчислення, але й операції з векторами і матрицями, комплексними числами, рядами та поліномами. Можна майже миттєво задати і вивести графіки різних функцій, від простої синусоїди до складної тривимірної фігури. Цей процес супроводжується звуковою анімацією. Робота із системою в режимі прямих обчислень носить діалоговий характер.


