Риск и способы его минимизации

В условиях асимметричности информации и неопределен­ности люди в осуществлении своей экономической деятельно­сти неизбежно идут па риск.

Под риском понимается ситуация, когда, зная вероятность каж­дого возможного исхода, нельзя точно предсказать конечный ре­зультат.

Рассмотрим некоторые основные понятия, связанные с по­ведением человека в условиях неопределенности. Участие в лотерее — типичный пример рисковой деятельности.

Ожидаемое значение случайной величины (например, вы­игрыш или проигрыш и лотерее) подсчитывается по формуле математического ожидания [7, c. 387; 10, с. 227]:

 

Е(х) = π ₁x₁ + π ₂x₂+... + π _n х_n,

 

где π ₁, π ₂,... -, π _n— вероятности каждого исхода;

x₁, x₂..., x_n — значения каждого исхода.

При этом важно учитывать, что вероятности могут иметь различную природу, т.е. быть как объективными, так и субъек­тивными.

Те ученые, которые придерживаются концепции объектив­ной природы вероятностей, полагают, что значения вероятно­стей потенциально определимы на математической основе. Так, французский астроном, математик и физик Пьер Лаплас определял вероятность исследуемого события как отношение количества благоприятных исходов данного события к количе­ству всех возможных исходов.

Сторонники субъективного подхода, например американ­ский экономист и статистик Леонард Сэвидж, полагали, что вероятности — это степени убежденности в наступлении тех или иных событий.

В любом случае будем исходить из того, что инди­вид стремится максимизировать свою ожидаемую полезность.

Истоки математического обоснования теории ожидаемой полезности можно встретить в работах швейцарских математи­ков Габриэля Крамера и Даниила Бернулли, которые стреми­лись объяснить знаменитый Санкт-Петербургский парадокс [10, c. 227-228].

Этот парадокс формулируется следующим образом: инди­виды готовы заплатить всего лишь небольшую сумму денег за участие в игре, в которой математическое ожидание выигрыша неопределенно велико. Игра заключается в подбрасывании монеты до тех пор, пока не выпадет заданная се сторона, на­пример, «орел», а размер выигрыша определяется количеством подбрасываний монеты до выпадения заданной стороны. Если потребуются всего два броска, выигрыш будет равен 2², если три броска — 2³, если n бросков, то выигрыш составит 2ⁿ. Ожи­даемый денежный выигрыш в такой игре бесконечен, однако большинство уклоняется от участия в ней.

Чтобы объяснить Санкт-Петербургский парадокс, Бернул­ли предположил, что в данном случае индивиды максимизируют не ожидаемый денежный выигрыш, а ожидаемую полезность. Бернулли не ставил вопрос о рациональности поведения инди­вида, но дал описательную модель ожидаемой полезности.

В дальнейшем идеи Бернулли получили развитие в работах американских экономистов Джона фон Неймана и Оскара Моргенштерна, которых часто называют основоположниками теории ожидаемой полезности. Они показали, что в условиях неполной информации рациональным выбором индивида бу­дет выбор с максимальной ожидаемой полезностью.

Ожидаемая полезность каждого варианта подсчитывается следующим образом:

_n

Е(U) = ∑ u_{i i}

^i-1

где u_i — полезность исхода;

_i — вероятность исхода;

n— число исходов.

Затем индивид сравнивает ожидаемые полезности вариан­тов и осуществляет выбор, стремясь максимизировать ожидае­мую полезность. Каково же будет его отношение к риску?

Людям свойственно различное отношение к риску [10, c. 228].

В экономической теории принято выделять лиц:

а) нейтральных к риску;

б) любителей риска;

в) испытывающих антипатию к риску или противников риска.

В некоторых случаях математическое ожидание при осуще­ствлении рисковой деятельности может быть равно в денеж­ном выражении нерисковому варианту, и все же люди поведут себя по-разному.

Например, ваш должник, вместо того чтобы вернуть вам 20 долл., предлагает бросить монету. Если вы выиграете, то получите не 20, а 40 долл. (т.е. ваш чистый выигрыш составит 20 долл.), но если проиграете — не получите ничего (т.е. потеряете свои 20 долл.). Математическое ожидание Е(х) в этом случае составит 0, 5 х 20 + 0, 5 х (—20) = 0, т.е. равно нулю, и получается, что вам вроде бы безразлично, играть в «орлянку» с должником или просто потребовать назад свои деньги.

Но кто-то пожелает пойти на риск в надежде получить больше, а кто-то предпочтет не предпринимать никаких дейст­вий, связанных с риском.

Практика показывает, что в основной массе люди не склон­ны к рисковой деятельности. Такое поведение обычно объясня­ется помимо особенностей человеческой психики чисто эко­номической причиной, а именно: действием закона убываю­щей предельной полезности.

Графически это отражено на рис. 37.

	Общая полезность

 

 

Рис. 37. График кривой полезности: нерасположенность к риску

 

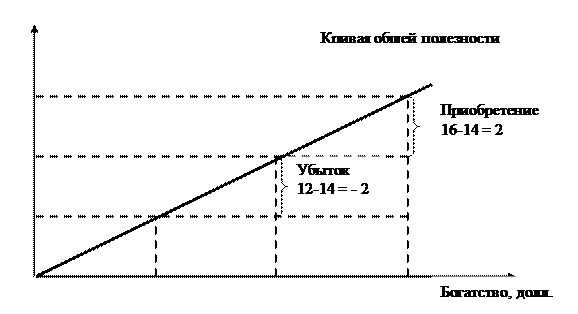
Предположим, что у вас есть 200 долл. Вы можете сыграть в рулетку и поставить «на красное» 100 долл. В случае выигрыша (при удачной игре «на цвет» сумма ставки увеличивается в два раза) у нас будет 300 долл.: 100 долл., которые вы не ставили, плюс 100 долл. × 2 — ваш выигрыш. То есть вы увеличите свое первоначальное богатство, равное 200 долл., на 100 долл. В слу­чае проигрыша у вас останется всего 100 долл., то есть вы уменьшите свое первоначальное богатство на 100 долл. Матема­тическое ожидание в денежном выражении:

0, 5 х (-100) + (0, 5 х 100) = 0.

Но предельная полезность, как видно из графика общей по­лезности, убывает, поэтому в условных единицах полезности ма­тематическое ожидание будет иметь отрицательное значение:

0, 5 х (-2) + 0, 5 х 1 =-1.

Иначе говоря, в случае проигрыша ваши убытки будут в ус­ловных единицах полезности больше, чем ваше приобретение в случае выигрыша.

Таким образом, в категориях предельных величин ситуация выглядит иначе, чем в денежном исчислении, и вы не будете склонны рисковать. В экономической теории данный феномен получил назва­ние эффекта владения. Эффект владения заключается в том, что люди гораздо выше оценивают то, чем они владеют, чем то, что пока им не принадлежит.

Существуют люди, которые все же склонны идти на риск. Само понятие предпринимательства всегда связано с большим или меньшим риском. Для таких людей, испытываю­щих склонность к риску, кривая общей полезности будет при­обретать вогнутый вид, и приобретение в случае выигрыша будет превышать убыток в случае проигрыша и условных едини­цах полезности (рис. 38)

	Общая полезность

 

Рис. 38. График кривой полезности: склонность к риску.

 

Математическое ожидание в денежном выражении, как и в случае, рассмотренном выше, будет:

0, 5 х (-100) + 0, 5 х 100 = 0

Но предельная полезность в данном случае возрастает, по­этому и условных единицах полезности математическое ожи­дание будет иметь положительное значение:

0, 5 х (-1) + 0, 5 х 5 = 2.

Положительный знак говорит о том, что для людей, склон­ных к рисковой деятельности, ощутимее будет радость выиг­рыша, чем неудовольствие от проигрыша.

Общая полезность

В случае нейтрального отношения к риску кри­вая обшей полезности будет приобретать вид прямой линии (рис. 39):

 

 

Рис. 39. Кривая полезности: нейтральное отношение к риску

 

Математическое ожидание в денежном выражении, естест­венно, не меняется:

0, 5 х (-100) + 0, 5 х 100 = 0.

Но и предельная полезность не меняется. Поэтому в услов­ных единицах полезности математическое ожидание также бу­дет равно нулю:

0, 5 х (-2) + 0, 5 х 2 = 0.

Таким образом, мы видим, что для людей, безразличных к риску, положительные эмоции от выигрыша равны отрица­тельным эмоциям от проигрыша.

С точки зрения теории ожидаемой полезности все три рас­смотренные варианта выбора будут рациональными.

М. Фридмен и Л. Сэвидж в своей статье «Анализ полезно­сти при выборе альтернатив, предполагающих риск» связыва­ют склонность или антипатию к риску с уровнем доходов раз­личных лиц и строят следующую кривую полезности [10, c. 232]:

Рис. 40. Кривая полезности: изменение отношения к риску в зависимости от уровня дохода: участок А – группа лиц с низкими доходами; участок В – промежуточная группа; участок С – группа лиц с высокими доходами.

Лица, принадлежащие к группам А и С, испытывают обыч­ную антипатию к риску. Лица группы В склонны к риску, по­скольку они не успели привыкнуть к богатству, недавно перей­дя из группы А, но у них есть шанс попасть в группу С. Группа В немногочисленна, так как из-за своего стремления к риску лица этой группы быстро переходят в группу А или в группу С. В данном случае рациональность поведения в отношении рис­ка зависит от фактического дохода, или благосостояния.

Есть и другие факты, противоречащие концепции ожидае­мой полезности. Однако данная концепция остается основной при оценке рационального выбора и условиях неполноты ин­формации.

Итак, подавляющая масса людей стремится максимально снизить риск, так как относится к категории противников риска.

Существует несколько способов снизить риск, или несколько способов страхования. Под страхованием понимается процедура, позволяющая индивиду обменять риск больших потерь на определенность малых [10, c. 233-234].

Объединение риска — это способ его снижения, при котором риск делится между несколькими участниками, так что в случае проигрыша потери, приходящиеся на долю каждого, не так ве­лики. На этом способе основывается существование различных коллективных фондов, касс взаимопомощи. Обычная страхо­вая компания в своей деятельности также использует объеди­нение риска: большое количество индивидов объединяют свой риск, уплачивая страховые взносы, а страховой случай имеет сравнительно небольшой процент и компенсируется из общей «кассы».

Распределение риска — способ страхования, применяемый в случае возможного крупного ущерба, когда одной компании не под силу взять па себя полностью обязательства по страхо­ванию.

Например, предприятие страхует свою деятельность от по­жара, причем размеры предприятия таковы, что возможные потери могут быть весьма существенными. Предприятий по­добного типа мало или рассматриваемое предприятие единично в своем роде, поэтому объединение рисков применить невоз­можно. Тогда оно обращается в крупную страховую ассоциа­цию, и риск возможной потери распределяется между компа­ниями, входящими в нес.

В таком случае каждая компания получает в качестве воз­награждения за участие в распределении рисков часть страхо­вого взноса страхующегося предприятия и принимает на себя обязательство в той же пропорции компенсировать ущерб от возможных потерь в случае пожара. Риск оказывается распре­деленным между рядом страховых компаний.

Диверсификация — способ, при котором экономические субъекты используют свои финансовые средства в разных сфе­рах, чтобы в случае потери в одной из них компенсировать это за счет другой сферы. Например, рекомендуется покупать ак­ции различных акционерных компаний, чтобы в случае потери ценности по части акций компенсировать это за счет роста курса акций другой или других компаний.

Страховые компании могут быть основаны на принципе объединения риска (взаимные страховые компании) или соз­даваться как обыкновенные акционерные компании. Во вто­ром случае речь идет о компаниях, ориентированных на полу­чение прибыли, первоначальный капитал которых образуется за счет вкладчиков-акционеров, а не за счет тех, кто будет пользоваться услугами компании.

Общий принцип страхования, который вытекает из его определения, следующий: вы жертвуете какой-то долей своего текущего потребления, чтобы в будущем избежать потери, ве­роятность которой достаточно велика.

Надо учитывать и тот факт, что есть виды деятельности, ко­торые связаны с нестрахуемыми рисками. При этом варианты нестрахуемых рисков могут нести как отрицательную, так и положительную нагрузку. Никто не застрахует вас, например, от ядерной войны или от всеобщей экологической катастрофы. Понятно, что, когда речь идет о катастрофах в рамках всего че­ловечества, нет такой страховой компании, которая приняла бы на себя ответственность за риски подобного рода. Это нега­тивные, но неизбежные варианты нестрахуемых рисков.

Однако есть другие примеры нестрахуемых рисков. Речь пойдет о предпринимательской деятельности. Сама суть пред­принимательства содержит в себе элемент риска, и говорить о его страховании просто неуместно. Поэтому можно сказать, что в данном случае факт нестрахуемости рисков является по­ложительным моментом.

Однако предприниматель, реализуя основную рисковую идею, может страховать отдельные аспекты своей деятельно­сти. Например, идя на риск при создании нового предприятия по производству пиломатериалов, он скорее всего постарается застраховать свои склады от пожаров, а рабочих — от травм в процессе производства. Но сама идея и ее реализации — сфор­мировать предприятие в данной отрасли — тем не менее оста­ются рисковыми.