Использование нечетких множеств рассмотрим при выводах на основе нечеткой логики. Нечеткая логика Пользуется различными критериями и условиями, получаемыми логическими способами. Ниже даны
Таблица 10.1. Многозначная логика

| Связка
| Обозначение
| Значения
|
| Тавтология
| 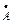
|
|
| Противоречие
| 
|
|
| Дизъюнкция
| 
|  , ,  + +  > 1
1, > 1
1,  + +  =1 =1
 , ,  + +  < 1 < 1
|
| Отрицание
| 
| 1- 
|
| Коньюнкция
| 
|  , ,  + +  < 1
0, < 1
0,  + +  =1 =1
 , ,  + +  > 1 > 1
|
| Импликация
| 
| 1-  , ,  < <  1,
1,  = = 
 , ,  > > 
|
| Эквивалентность
| 
| 1-   , ,  < <  1,
1,  = = 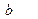 1-
1-   , ,  > > 
|
| Штрих Шеффера
| 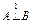
| 1-  , ,  + +  < 1
1, < 1
1,  + +  =1
1- =1
1-  , ,  + +  > 1 > 1
|
| Стрелка Пирса
| 
| 1-  , ,  + +  > 1
0, > 1
0,  + +  =1
1- =1
1-  , ,  + +  < 1 < 1
|
примеры наиболее широко используемых критериев.
Правила-критерии нечетких выводов для  Ì
Ì  ,
,  Ì
Ì  :
:
I. Пр1: если  есть
есть  , то
, то  есть
есть 
 Пр2:
Пр2:  есть
есть 
Сл:  есть
есть  .
.
II-1.Пр1: если  есть
есть  , то
, то  есть
есть 
Пр2:  есть очень
есть очень 
 Сл:
Сл:  есть очень
есть очень  .
.
II-2. Пр1: если

есть

, то

есть

Пр2:  есть очень
есть очень 
 Сл:
Сл:  есть
есть  .
.
III. Пр1: если  есть
есть  , то
, то  есть
есть 
 Пр2:
Пр2:  есть более или менее
есть более или менее 
Сл:  есть более или менее
есть более или менее  .
.
IV-1. Пр1: если  есть
есть  , то
, то  есть
есть 
Пр2:  есть не
есть не 
 Сл:
Сл:  неизвестно.
неизвестно.
IV-2. Пр1: если  есть
есть  , то
, то  есть
есть 
Пр2:  есть не
есть не 
 Сл:
Сл:  есть не
есть не  ,
,
где “Пр” – предпосылка, “Сл” – следствие,  =
=  (
( )/
)/  ,
,  =
= 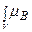 (
( )/
)/  , ”очень
, ”очень  ” =
” = 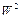 , “более или менее
, “более или менее  ” =
” =  (
( - любое нечеткое множество).
- любое нечеткое множество).
Условие-неравенство:  (
( )Ù (
)Ù ( (
( )
) 
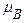 (
( ))£
))£ 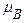 (
( ), где “
), где “  ” – импликация, зависящая от вида нечеткой логики
” – импликация, зависящая от вида нечеткой логики  .
.
Пример:  =
=  ,
,
 =
=  =0+1+2+3+4+5+6+7+8+9+10,
=0+1+2+3+4+5+6+7+8+9+10,
 =мало=1/0+0.8/1+0.6/2+0.4/3+0.2/4,
=мало=1/0+0.8/1+0.6/2+0.4/3+0.2/4,
 =средне=0.2/2+0.4/3+0.8/4+1/5+0.8/6+0.4/7+0.2/8.
=средне=0.2/2+0.4/3+0.8/4+1/5+0.8/6+0.4/7+0.2/8.
Проверим правило-критерий I. Для этого сначала найдем бинарное отношение  (
( (
( ),
),  (
( )) между
)) между  и
и  в предпосылке Пр1 (
в предпосылке Пр1 ( (
( ),
),  (
( ) – множества, определяемые атрибутами
) – множества, определяемые атрибутами  ,
,  , принимающими значения из
, принимающими значения из  ,
,  соответственно). Предпосылка Пр1 - “если
соответственно). Предпосылка Пр1 - “если  есть
есть  , то
, то  есть
есть  ” - содержит два унарных отношения:
” - содержит два унарных отношения: 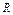 (
( (
( ))=
))=  и
и 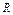 (
( (
( ))=
))=  . Из всех возможных отношений
. Из всех возможных отношений  (
( (
( ),
),  (
( )) выберем отношение вида
)) выберем отношение вида  (
( (
( ),
),  (
( )) =
)) = 


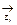


 = =
= =  (
( )
) 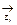
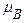 (
( ) ) /(
) ) /( ,
,  ), где
), где  (
( )
) 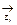
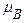 (
( )=
)=  (
( ,
,  ). Тогда с учетом табл.1.3, где
). Тогда с учетом табл.1.3, где  =
=  (
( ),
),  =
= 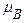 (
( ), можно рассчитать
), можно рассчитать  (
( (
( ),
),  (
( )) следующим образом:
)) следующим образом:
0
0.

=

=0,

=

=0. Из исходных данных

(

)=1 (числитель первого элемента множества

),

(

)=0 (то же для

). В этом случае

>

и

(

,

)=

(

)
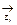

(

)=1
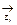
0=0.
10.  =
=  =0,
=0,  =
=  =1;
=1;  (
( )=1,
)=1,  (
( )=0;
)=0;  (
( ,
,  )=0.
)=0.
20.  =
=  =0,
=0,  =
= 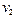 =2;
=2;  (
( )=1,
)=1,  (
(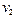 )=0.2;
)=0.2;  (
( ,
, 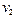 )=0.2 и т. д.
)=0.2 и т. д.
01.  =
=  =1,
=1,  =
=  =0;
=0;  (
( )=0.8,
)=0.8,  (
( )=0;
)=0;  (
( ,
,  )=0 и
)=0 и
т. д.
Значения  для всех пар (
для всех пар ( ,
,  ) сведем в таблицу отношения
) сведем в таблицу отношения  (
( (
( ),
),  (
( )) – табл.10.2.
)) – табл.10.2.
Таблица 10.2. Значения  (
( (
( ),
),  (
( ))
))

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0.2
| 0.4
| 0.8
|
| 0.8
| 0.4
| 0.2
|
|
|
|
|
|
| 0.2
| 0.4
|
| 0.2
|
| 0.4
| 0.2
|
|
|
|
|
|
| 0.2
| 0.4
| 0.4
| 0.4
| 0.4
| 0.4
| 0.2
|
|
|
|
|
|
| 0.2
|
| 0.6
| 0.6
| 0.6
|
| 0.2
|
|
|
|
|
|
|
| 0.8
| 0.8
| 0.8
| 0.8
| 0.8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предпосылка Пр2 есть 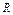 (
( (
( ))=
))=  . Тогда следствие
. Тогда следствие 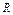 (
( (
( ))= =
))= = 

 (
( (
( ),
),  (
( ))=
))= 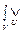 [
[  (
( )Ù (
)Ù ( (
( )
) 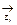
 (
( ))]/
))]/  =
= 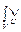 [
[  (
( )Ù
)Ù
Ù  (
( ,
,  )]/
)]/  , где
, где  [
[  (
( )Ù
)Ù  (
( ,
,  )]=
)]=  (
( ). По аналогии с предыдущим алгоритмом имеем:
). По аналогии с предыдущим алгоритмом имеем:
00.  =
=  =0,
=0,  =
=  =0;
=0;  (
( )=1,
)=1,  (
( ,
,  )=0. В этом случае
)=0. В этом случае
 (
( )Ù
)Ù  (
( ,
,  )=1Ù 0=0=
)=1Ù 0=0=  .
.
1
0.

=

=1,

=

=0;

(

)=0.8,

(

,

)=0;

=0.8Ù 0=0 и т. д.
50.  =
=  =5,
=5,  =
=  =0;
=0;  (
( )=0,
)=0,  (
( ,
,  )=1;
)=1; 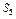 =0Ù 1=0 и т. д.
=0Ù 1=0 и т. д.
Очевидно, что  (
( )=
)=  [
[  (
( )Ù
)Ù  (
( ,
,  )]=0. Аналогично находим
)]=0. Аналогично находим  (
( )=0. Далее:
)=0. Далее:
02.  =
=  =0,
=0,  =
= 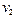 =2;
=2;  (
( )=1,
)=1,  (
( ,
, 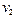 )=0.2;
)=0.2;  (
( )Ù
)Ù  (
( ,
, 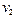 )=1Ù 0.2=0.2=
)=1Ù 0.2=0.2=  .
.
12.  =
=  =1,
=1,  =
= 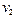 =2;
=2;  (
( )=0.8, (
)=0.8, (
 ,
, 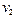 )=0.2;
)=0.2;  =0.8Ù 0.2=0.2;
=0.8Ù 0.2=0.2;
42.  =
=  =4,
=4,  =
= 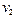 =2;
=2;  (
( )=0.2,
)=0.2,  (
( ,
, 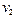 )=1;
)=1;  =0.2Ù 1=0.2.
=0.2Ù 1=0.2.
52.  =
=  =5,
=5,  =
= 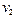 =2;
=2;  (
( )=0,
)=0,  (
( ,
, 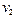 )=1;
)=1; 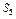 =0Ù 1=0 и т. д. до
=0Ù 1=0 и т. д. до 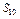 =0. Для этих пунктов
=0. Для этих пунктов  (
(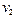 )=
)=  [
[  (
( )Ù
)Ù 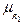 (
( ,
,  )]=0.2. После нахождения всех значений
)]=0.2. После нахождения всех значений  (
( ) имеем:
) имеем:
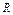 (
( (
( ))=0.2/2+0.4/3+0.8/4+1/5+0.8/6+0.4/7+0.2/8 =
))=0.2/2+0.4/3+0.8/4+1/5+0.8/6+0.4/7+0.2/8 =  = средне.
= средне.

 есть
есть  , то
, то  есть
есть 
 =
=  =0,
=0,  =
=  =0. Из исходных данных
=0. Из исходных данных  (
( )=1 (числитель первого элемента множества
)=1 (числитель первого элемента множества  ),
),  (
( )=0 (то же для
)=0 (то же для  ). В этом случае
). В этом случае  >
>  и
и  (
( ,
,  )=
)=  (
( )
) 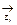
 (
( )=1
)=1 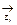 0=0.
0=0.
 =
=  =1,
=1,  =
=  =0;
=0;  (
( )=0.8,
)=0.8,  (
( ,
,  )=0;
)=0;  =0.8Ù 0=0 и т. д.
=0.8Ù 0=0 и т. д.

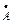





 1,
1, 

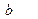 1-
1- 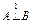

 ,
,  :
: Пр2:
Пр2:  Сл:
Сл:  Сл:
Сл:  Пр2:
Пр2:  Сл:
Сл:  Сл:
Сл:  (
(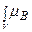 (
( ” =
” = 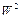 , “более или менее
, “более или менее  (
( (
(
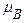 (
( .
. (
( (
( (
(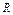 (
(
 (
( (
( =1;
=1; 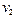 =2;
=2; 

 . Тогда следствие
. Тогда следствие 
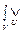 [
[ 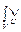 [
[  [
[  (
( .
.
 =5,
=5, 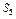 =0Ù 1=0 и т. д.
=0Ù 1=0 и т. д.
 =4,
=4,  =0.2Ù 1=0.2.
=0.2Ù 1=0.2.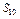 =0. Для этих пунктов
=0. Для этих пунктов 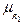 (
( )]=0.2. После нахождения всех значений
)]=0.2. После нахождения всех значений 


