Если остаточная погрешность  больше
больше  , то результат отбрасывается как грубая погрешность (
, то результат отбрасывается как грубая погрешность ( - сомнительный результат).
- сомнительный результат).
Критерий применяется при большом числе измерений.
Иногда пользуются критерием  . Если разность
. Если разность  >
>  , то результат
, то результат  принимают за грубую погрешность и отбрасывают.
принимают за грубую погрешность и отбрасывают.
8.2 Проверка нормальности результатов наблюдений
При числе результатов наблюдений 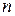 < 50 нормальность распределения проверяют при помощи составного критерия.
< 50 нормальность распределения проверяют при помощи составного критерия.
Критерий 1.
Вычисляют отношение 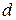 :
:
 ,
,
где  – смещенная оценка среднеквадратического отклонения, которая вычисляется по формуле
– смещенная оценка среднеквадратического отклонения, которая вычисляется по формуле
 .
.
Результаты наблюдений считаются нормально распределенными, если
 <
< 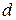 <
< 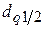 ,
,
где  и
и 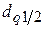 - квантили распределения, получаемые из табл. 8.3;
- квантили распределения, получаемые из табл. 8.3;  – заранее выбранный уровень значимости.
– заранее выбранный уровень значимости.
Таблица 8.3
Статистика 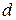
| 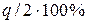
| 
|
| 1%
| 5%
| 95%
| 99%
|
|
| 0, 9137
| 0, 8884
| 0, 7236
| 0, 6829
|
|
| 0, 9001
| 0, 8768
| 0, 7304
| 0, 6950
|
|
| 0, 8901
| 0, 8686
| 0, 7360
| 0, 7040
|
|
| 0, 8826
| 0, 8625
| 0, 7404
| 0, 7110
|
|
| 0, 8769
| 0, 8578
| 0, 7440
| 0, 7167
|
|
| 0, 8722
| 0, 8540
| 0, 7470
| 0, 7216
|
|
| 0, 8682
| 0, 8508
| 0, 7496
| 0, 7256
|
|
| 0, 8648
| 0, 8481
| 0, 7518
| 0, 7291
|
Критерий 2.
По этому критерию результаты наблюдений принадлежат нормальному распределению, если не более  разностей
разностей  превзошли значение
превзошли значение 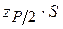 , где
, где 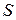 определяется по формуле
определяется по формуле
 ,
,
 – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности
– верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности 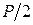 .
.
Значения  определяются из табл. 8.4 по выбранному уровню значимости
определяются из табл. 8.4 по выбранному уровню значимости  и числу результатов наблюдений
и числу результатов наблюдений 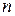 .
.
Если при проверке нормальности распределения для критерия 1 выбран уровень значимости  , а для критерия 2 –
, а для критерия 2 – 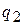 , то результирующий уровень значимости составного критерия будет
, то результирующий уровень значимости составного критерия будет  .
.
Распределение результатов наблюдений не соответствует нормальному в том случае, если не соблюдается хотя бы один из критериев.
Таблица 8.4
Значения  для вычисления
для вычисления 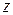
| 
| 
|
| 1%
| 2%
| 5%
|
|
|
| 0, 98
| 0, 98
| 0, 96
|
| 11 – 14
|
| 0, 99
| 0, 98
| 0, 97
|
| 15 – 20
|
| 0, 99
| 0, 99
| 0, 98
|
| 21 – 22
|
| 0, 98
| 0, 97
| 0, 96
|
|
|
| 0, 98
| 0, 98
| 0, 96
|
| 24 – 27
|
| 0, 98
| 0, 98
| 0, 97
|
| 28 – 32
|
| 0, 99
| 0, 98
| 0, 97
|
| 33 – 35
|
| 0, 99
| 0, 98
| 0, 98
|
| 36 – 49
|
| 0, 99
| 0, 99
| 0, 98
|
Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости от 10 до 2%.
При большом числе наблюдений (более 50) используются критерий согласия К.Пирсона (критерий  ) для группированных наблюдений и критерий Р.Мизеса – Н.В.Смирнова (критерий
) для группированных наблюдений и критерий Р.Мизеса – Н.В.Смирнова (критерий  ) для негруппированных наблюдений.
) для негруппированных наблюдений.
Метод  заключается в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом наблюдений, построенной на основе нормального распределения.
заключается в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом наблюдений, построенной на основе нормального распределения.
Порядок вычислений следующий:
1. Вычисляют среднее арифметическое результата измерений и оценку
среднеквадратического результата наблюдений.
2. Группируют наблюдения по интервалам. Для каждого интервала вычисляют середину  и подсчитывают эмпирическое число наблюдений
и подсчитывают эмпирическое число наблюдений 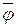 , попавшее в каждый интервал. При числе наблюдений 40 – 100 принимают 5 – 9 интервалов.
, попавшее в каждый интервал. При числе наблюдений 40 – 100 принимают 5 – 9 интервалов.
3. Вычисляют теоретически соответствующее нормальному распределению число наблюдений  для каждого интервала. Для этого из реальных середин интервалов
для каждого интервала. Для этого из реальных середин интервалов  переходят к нормированным
переходят к нормированным 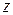 :
:
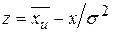 .
.
Затем для каждого значения 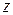 находят значение функции плотности вероятностей
находят значение функции плотности вероятностей  :
:
 .
.
4. Вычисляют ту часть  общего числа имеющихся наблюдений, которая теоретически должна была быть в каждом из интервалов:
общего числа имеющихся наблюдений, которая теоретически должна была быть в каждом из интервалов:
 ,
,
где 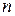 - общее число наблюдений;
- общее число наблюдений; 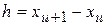 - длина интервала, принятая при построении гистограммы.
- длина интервала, принятая при построении гистограммы.
5. Если в какой-либо интервал теоретически попадает меньше наблюдений, то его в обеих гистограммах соединяют с соседним интервалом.
6. Определяют число степеней свободы  , где
, где 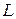 – общее число интервалов после укрупнения.
– общее число интервалов после укрупнения.
7. Вычисляют показатель разности частот  :
:
 ,
,
где  .
.
8. Выбирают уровень значимости (от 0, 02≤  ≤ 0, 1%). По уровню значимости и числу степеней свободы
≤ 0, 1%). По уровню значимости и числу степеней свободы 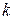 находят границу критической области
находят границу критической области 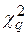 . Если оказывается, что
. Если оказывается, что  >
> 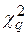 , то гипотеза о нормальности отвергается.
, то гипотеза о нормальности отвергается.
8.3 Определение доверительных границ случайной и неисключенной систематической погрешности результата измерения
Доверительные границы случайной погрешности результата измерения устанавливаются для результатов наблюдений, принадлежащих нормальному распределению. Они без учета знака определяются выражением
 ,
,
где  – коэффициент Стьюдента, который зависит от заданной доверительной вероятности
– коэффициент Стьюдента, который зависит от заданной доверительной вероятности  и числа результатов наблюдений. Доверительную вероятность
и числа результатов наблюдений. Доверительную вероятность  принимают равной 0, 95; допускается указывать границы для
принимают равной 0, 95; допускается указывать границы для  .
.
Доверительные границы неисключенной систематической погрешности  результата измерений вычисляют путем построения композиции распределения составляющих неисключенных систематических погрешностей. При равномерном распределении эти границы вычисляются по формуле
результата измерений вычисляют путем построения композиции распределения составляющих неисключенных систематических погрешностей. При равномерном распределении эти границы вычисляются по формуле
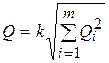 ,
,
где 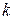 – коэффициент, определяемый принятой доверительной вероятностью, равный 1, 1 при
– коэффициент, определяемый принятой доверительной вероятностью, равный 1, 1 при 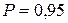 и 1, 4 – при
и 1, 4 – при  и
и  > 4;
> 4;  – число суммируемых неисключенных погрешностей.
– число суммируемых неисключенных погрешностей.
Если  < 4, то коэффициент
< 4, то коэффициент 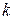 определяют по данному графику зависимости
определяют по данному графику зависимости  ,
, 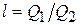 . За
. За  принимается наиболее отличающаяся от других составляющая, в качестве
принимается наиболее отличающаяся от других составляющая, в качестве  следует принимать ближайшую в составляющую.
следует принимать ближайшую в составляющую.
При определении границы погрешности результата измерения рассматривают соотношение неисключенной систематической и случайной погрешностей.
Если неисключенные систематические погрешности пренебрежимо малы по сравнению со случайными (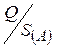 < 0, 8), то погрешность результата измерения можно характеризовать только доверительными границами случайной погрешности, т.е.
< 0, 8), то погрешность результата измерения можно характеризовать только доверительными границами случайной погрешности, т.е.  .
.
Если пренебрежимо малы случайные погрешности (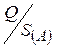 > 8), то погрешность результата измерения характеризуется неисключенными систематическими погрешностями
> 8), то погрешность результата измерения характеризуется неисключенными систематическими погрешностями  .
.
Если 0, 8 < 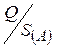 < 8, то граница погрешности результата измерения вычисляется по формуле
< 8, то граница погрешности результата измерения вычисляется по формуле 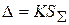 , где
, где 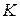 – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
– коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;  – оценка суммарного среднеквадратического отклонения результата измерения, вычисляемая по формуле
– оценка суммарного среднеквадратического отклонения результата измерения, вычисляемая по формуле
 .
.
Коэффициент 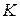 определяют по зависимости
определяют по зависимости
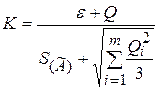 .
.
Результаты измерения должны быть представлены в стандартной форме. Так, при симметричной доверительной погрешности указывают: результат 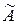 , граница погрешности
, граница погрешности  и вероятность
и вероятность  :
:
 .
.
Численное значение результата 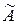 должно оканчиваться цифрой того же разряда, что и значение погрешности.
должно оканчиваться цифрой того же разряда, что и значение погрешности.
При необходимости дальнейшей обработки результатов или анализа погрешности результаты измерения представляются в форме 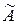 ,
,  ,
, 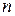 ,
,  . Иногда указывают и доверительную вероятность
. Иногда указывают и доверительную вероятность  .
.
Приложение 1.

 больше
больше  , то результат отбрасывается как грубая погрешность (
, то результат отбрасывается как грубая погрешность ( - сомнительный результат).
- сомнительный результат). . Если разность
. Если разность 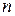 < 50 нормальность распределения проверяют при помощи составного критерия.
< 50 нормальность распределения проверяют при помощи составного критерия.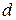 :
: ,
, – смещенная оценка среднеквадратического отклонения, которая вычисляется по формуле
– смещенная оценка среднеквадратического отклонения, которая вычисляется по формуле .
. <
< 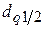 ,
, – заранее выбранный уровень значимости.
– заранее выбранный уровень значимости.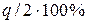

 разностей
разностей  превзошли значение
превзошли значение 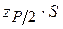 , где
, где 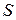 определяется по формуле
определяется по формуле ,
, – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности
– верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности 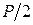 .
. определяются из табл. 8.4 по выбранному уровню значимости
определяются из табл. 8.4 по выбранному уровню значимости  , а для критерия 2 –
, а для критерия 2 – 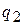 , то результирующий уровень значимости составного критерия будет
, то результирующий уровень значимости составного критерия будет  .
.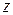

 ) для группированных наблюдений и критерий Р.Мизеса – Н.В.Смирнова (критерий
) для группированных наблюдений и критерий Р.Мизеса – Н.В.Смирнова (критерий  ) для негруппированных наблюдений.
) для негруппированных наблюдений. и подсчитывают эмпирическое число наблюдений
и подсчитывают эмпирическое число наблюдений 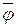 , попавшее в каждый интервал. При числе наблюдений 40 – 100 принимают 5 – 9 интервалов.
, попавшее в каждый интервал. При числе наблюдений 40 – 100 принимают 5 – 9 интервалов. для каждого интервала. Для этого из реальных середин интервалов
для каждого интервала. Для этого из реальных середин интервалов 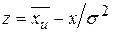 .
. :
: .
. ,
,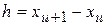 - длина интервала, принятая при построении гистограммы.
- длина интервала, принятая при построении гистограммы. , где
, где 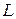 – общее число интервалов после укрупнения.
– общее число интервалов после укрупнения. ,
, .
.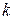 находят границу критической области
находят границу критической области 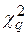 . Если оказывается, что
. Если оказывается, что  ,
, – коэффициент Стьюдента, который зависит от заданной доверительной вероятности
– коэффициент Стьюдента, который зависит от заданной доверительной вероятности  принимают равной 0, 95; допускается указывать границы для
принимают равной 0, 95; допускается указывать границы для  .
. результата измерений вычисляют путем построения композиции распределения составляющих неисключенных систематических погрешностей. При равномерном распределении эти границы вычисляются по формуле
результата измерений вычисляют путем построения композиции распределения составляющих неисключенных систематических погрешностей. При равномерном распределении эти границы вычисляются по формуле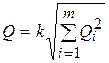 ,
,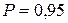 и 1, 4 – при
и 1, 4 – при  ,
, 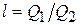 . За
. За  принимается наиболее отличающаяся от других составляющая, в качестве
принимается наиболее отличающаяся от других составляющая, в качестве  следует принимать ближайшую в составляющую.
следует принимать ближайшую в составляющую.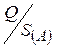 < 0, 8), то погрешность результата измерения можно характеризовать только доверительными границами случайной погрешности, т.е.
< 0, 8), то погрешность результата измерения можно характеризовать только доверительными границами случайной погрешности, т.е.  .
. .
.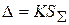 , где
, где 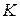 – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
– коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;  – оценка суммарного среднеквадратического отклонения результата измерения, вычисляемая по формуле
– оценка суммарного среднеквадратического отклонения результата измерения, вычисляемая по формуле .
.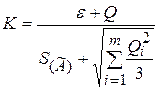 .
.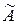 , граница погрешности
, граница погрешности  и вероятность
и вероятность  .
. ,
, 


