Основные теоретические положения. 3.1.1. Параметры замедляющих систем
3.1.1. Параметры замедляющих систем Замедляющими системами (ЗС) называются линии передачи, в которых возможно распространение медленных электромагнитных волн, т. е. волн, фазовая скорость которых меньше скорости света в среде, заполняющей 3С. В настоящее время ЗС широко используются для осуществления длительного взаимодействия заряженных частиц с электромагнитными волнами в электронных приборах СВЧ и линейных ускорителях заряженных частиц при условии синхронизма скорости электронного потока и фазовой скорости электромагнитного поля. Кроме того, замедляющие системы используются в параметрических и квантовых парамагнитных усилителях бегущей волны, для создания линий задержки, фильтров и ряда других устройств. Как правило, замедляющие системы являются периодическими структурами, т. е. совмещаются сами с собой при перемещении вдоль продольной оси Одной из основных характеристик волны, распространяющейся в ЗС, является сдвиг фаз Электромагнитное поле волны, распространяющейся в периодической структуре, можно представить в виде разложения по пространственным гармоникам. Это разложение для продольной составляющей электрического поля ЗС имеет вид
где
и групповую
скорости Как видно из этих выражений, фазовые скорости пространственных гармоник различны по величине и направлению, в то время как групповая скорость всех гармоник одинакова. Пространственные гармоники, у которых направления фазовой и групповой скоростей совпадают, называются прямыми, а те, у которых они противоположны, – обратными.
Зависимость фазовой и групповой скоростей пространственных гармоник от частоты 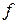 или длины волны или длины волны 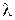 называется дисперсионной характеристикой (ДХ) замедляющей системы. Наиболее удобно представлять дисперсионную характеристику в виде зависимости волнового числа от постоянной фазы называется дисперсионной характеристикой (ДХ) замедляющей системы. Наиболее удобно представлять дисперсионную характеристику в виде зависимости волнового числа от постоянной фазы 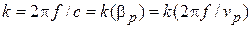 или зависимости параметра замедления фазовой скорости или зависимости параметра замедления фазовой скорости 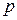 -й пространственной гармоники от длины волны -й пространственной гармоники от длины волны 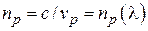 . .
Дисперсионная характеристика первого вида (называемая также диаграммой Бриллуэна) изображена на рис. 3.1. Как видно на рисунке, распространение волн в периодических структурах возможно в определенных диапазонах частот (волновых чисел), называемых полосами пропускания, или полосами прозрачности. Каждой такой полосе соответствует определенный тип волны, распространяющейся в ЗС. В зависимости от типа ЗС нижняя полоса пропускания может начинаться как от нулевой частоты, так и от некоторого ненулевого значения. В каждой полосе прозрачности сплошная линия относится к падающей волне, а штриховая – к отраженной. Указываются также номера пространственных гармоник этих волн. Обычно левую часть графика, т. е. функцию
где Второй тип дисперсионной характеристики, построенной для той же ЗС, показан на рис. 3.2. Так как по оси ординат откладывается непосредственно замедление, этот тип дисперсионной характеристики наиболее часто используется при анализе работы ЗС в электронных приборах СВЧ, хотя дисперсионные кривые в координатах Для построения дисперсионной характеристики второго типа необходимо провести линии
описываемые уравнением
нанести на них соответствующие значения длин волн Важным параметром замедляющей системы является сопротивление связи
где Распространение волны в ЗС сопровождается ее затуханием вследствие потерь в стенках. Постоянная затухания
На практике для характеристики затухания (потерь) обычно указывают величину
3.2.2. Измерение характеристик и параметров ЗС В работе для измерения характеристик и параметров ЗС используется резонансный метод измерения, основанный на исследовании короткозамкнутого отрезка ЗС. Резонанс в таком отрезке линии передачи наблюдается, когда вдоль его длины
Определив резонансные частоты В соответствии с теоремой возмущений можно записать
где Из формулы следует, что относительное значение продольной составляющей электрического поля пропорционально квадратному корню из ухода частоты
где Коэффициенты ряда Фурье (3.1) определяются по известной формуле для четной относительно начала координат функции:
Используя затем выражения – и учитывая, что
получим
Множитель 4 в знаменателе (3.10) учитывает, что в закороченном отрезке ЗС возбуждаются падающая и отраженная волны с одинаковыми амплитудами, в результате чего максимальная амплитуда поля и запасенная энергия в макете удваиваются. На границах полосы пропускания сопротивление связи теряет смысл, так как групповая скорость обращается в ноль. Измерив Для определения коэффициента
где
Измерение затухания основано на определении добротности
Определение добротности производится по ширине резонансной характеристики макета
|

 на некоторое расстояние
на некоторое расстояние 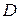 , называемое периодом ЗС. Наряду с этим ЗС могут содержать и другие элементы симметрии, которые во многом определяют характер распространения в них электромагнитных волн.
, называемое периодом ЗС. Наряду с этим ЗС могут содержать и другие элементы симметрии, которые во многом определяют характер распространения в них электромагнитных волн.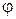 электромагнитного поля в поперечных сечениях, отстоящих друг от друга на период. Физически различаются углы фазового сдвига, лежащие в промежутке (
электромагнитного поля в поперечных сечениях, отстоящих друг от друга на период. Физически различаются углы фазового сдвига, лежащие в промежутке (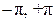 ), причем положительным и отрицательным значениям угла
), причем положительным и отрицательным значениям угла 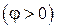 условимся считать падающей, a c отрицательным (
условимся считать падающей, a c отрицательным ( ) – отраженной. Поскольку свойства падающей и отраженной волн одинаковы, достаточно рассмотреть только одну, например падающую, волну, что сужает диапазон изменения угла фазового сдвига промежутком (
) – отраженной. Поскольку свойства падающей и отраженной волн одинаковы, достаточно рассмотреть только одну, например падающую, волну, что сужает диапазон изменения угла фазового сдвига промежутком ( ).
).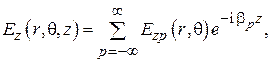
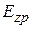 – амплитуды пространственных гармоник;
– амплитуды пространственных гармоник;  – их фазовые постоянные, определяющие фазовую
– их фазовые постоянные, определяющие фазовую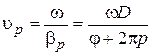
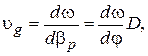
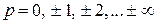 ).
).
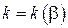 при
при 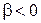 , изображают на правой части характеристики, зеркально отражая ее относительно оси ординат. Нетрудно видеть, что в любой точке диаграммы Бриллуэна
, изображают на правой части характеристики, зеркально отражая ее относительно оси ординат. Нетрудно видеть, что в любой точке диаграммы Бриллуэна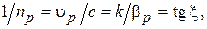
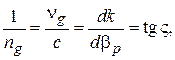
 и
и 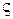 – углы наклона секущей и касательной к дисперсионной характеристике в данной точке (рис. 2.1);
– углы наклона секущей и касательной к дисперсионной характеристике в данной точке (рис. 2.1); 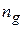 – замедление групповой скорости.
– замедление групповой скорости. ,
, 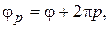
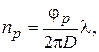
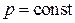 . Полученная кривая изображает дисперсию пространственной гармоники с номером
. Полученная кривая изображает дисперсию пространственной гармоники с номером 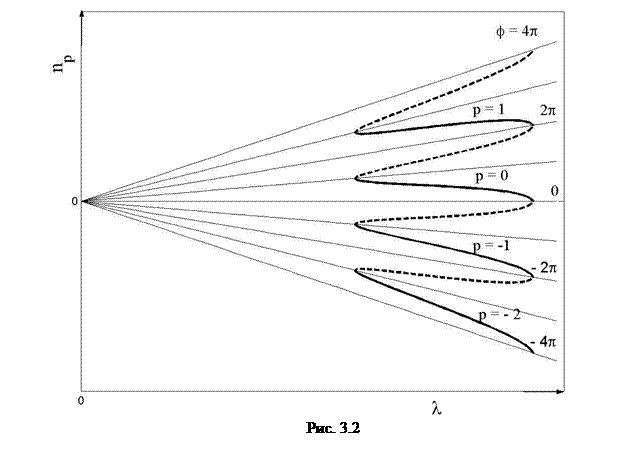
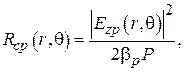
 амплитуда продольной составляющей электрического поля
амплитуда продольной составляющей электрического поля 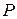 – мощность, проходящая через поперечное сечение ЗС;
– мощность, проходящая через поперечное сечение ЗС;  – фазовая постоянная данной пространственной гармоники.
– фазовая постоянная данной пространственной гармоники. определяется мощностью потерь на единицу длины замедляющей системы
определяется мощностью потерь на единицу длины замедляющей системы 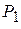 :
: .
.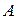 – затухание замедляющей системы в децибелах на единицу длины, связанную с постоянной затухания
– затухание замедляющей системы в децибелах на единицу длины, связанную с постоянной затухания  .
.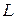 укладывается целое число
укладывается целое число 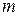 полуволн. Если отрезок ЗС имеет
полуволн. Если отрезок ЗС имеет  периодов (
периодов (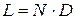 ), это условие резонанса принимает вид
), это условие резонанса принимает вид 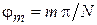 . Поскольку, как уже отмечалось
. Поскольку, как уже отмечалось 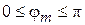 , на каждом типе волны в отрезке ЗС может наблюдаться
, на каждом типе волны в отрезке ЗС может наблюдаться 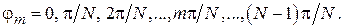
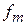 , волновые числа
, волновые числа 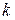 и длины волн
и длины волн 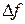 отрезка ЗС при протягивании вдоль его оси малого возмущающего тела.
отрезка ЗС при протягивании вдоль его оси малого возмущающего тела.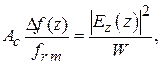
 – калибровочный коэффициент, зависящий от формы и размеров возмущающего тела;
– калибровочный коэффициент, зависящий от формы и размеров возмущающего тела; 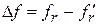 – изменение резонансной частоты, равное разности резонансной частоты без возмущающего тела
– изменение резонансной частоты, равное разности резонансной частоты без возмущающего тела  и резонансной частоты с возмущающим телом
и резонансной частоты с возмущающим телом 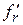 ;
;  – продольная составляющая электрического поля;
– продольная составляющая электрического поля; 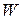 – энергия, запасенная в исследуемом макете ЗС.
– энергия, запасенная в исследуемом макете ЗС.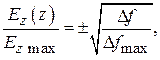
 – максимальный уход частоты, зарегистрированный при протягивании возмущающего тела.
– максимальный уход частоты, зарегистрированный при протягивании возмущающего тела.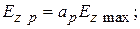
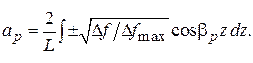
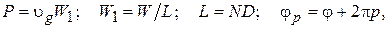
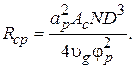
 (в относительных единицах) и определить число полуволн, укладывающихся на длине отрезка ЗС. Для получения достаточной точности необходимо, чтобы размер (длина) возмущающего тела
(в относительных единицах) и определить число полуволн, укладывающихся на длине отрезка ЗС. Для получения достаточной точности необходимо, чтобы размер (длина) возмущающего тела 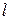 и шаг перемещения
и шаг перемещения  были в несколько раз меньше
были в несколько раз меньше 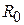 и длиной
и длиной 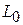 для вида колебаний
для вида колебаний  калибровочный коэффициент
калибровочный коэффициент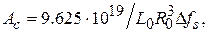
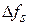 – изменение резонансной частоты эталонного резонатора при помещении возмущающего тела. Групповая скорость вычисляется путем дифференцирования дисперсионной характеристики
– изменение резонансной частоты эталонного резонатора при помещении возмущающего тела. Групповая скорость вычисляется путем дифференцирования дисперсионной характеристики 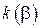 (см. рис. 3.1). Поскольку экспериментальные точки на этой характеристике расположены сравнительно редко (вследствие сравнительно малого числа периодов в отрезке ЗС), численное дифференцирование дает большую погрешность. Поэтому необходимо аппроксимировать зависимость
(см. рис. 3.1). Поскольку экспериментальные точки на этой характеристике расположены сравнительно редко (вследствие сравнительно малого числа периодов в отрезке ЗС), численное дифференцирование дает большую погрешность. Поэтому необходимо аппроксимировать зависимость 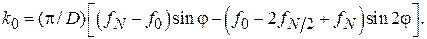
 короткозамкнутого отрезка ЗС на виде колебаний, соответствующем данному углу фазового сдвига
короткозамкнутого отрезка ЗС на виде колебаний, соответствующем данному углу фазового сдвига  . Постоянная затухания определяется по формуле
. Постоянная затухания определяется по формуле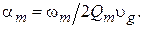
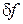 на уровне половинной мощности:
на уровне половинной мощности: 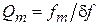 .
.


