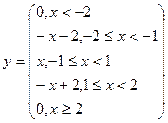Задача 2.1. Вычисление значения функции, заданной графически
Написать программу, которая по введенному значению аргумента вычисляет значение функции, заданной в виде графика (рис. 2.1).
Рис. 2.1. Функция для задачи 2.1
Начинать решение даже простейшей задачи необходимо с четкого описания того что является ее исходными данными и результатами. В данном случае это очевидно: исходными данными является вещественное значение аргумента х, который определен на всей числовой оси, а результатом - вещественное значение функции y.
Перед написанием программы следует составить алгоритм ее решения - сначала в общем виде, а затем постепенно детализируя каждый шаг. Такой способ, называемый «нисходящая разработка», позволяет создавать простые по структуре программы. По мере приобретения опыта вы убедитесь, насколько это важно. Как известно, алгоритм решения задачи можно описать в различном виде, например, в словесном или в виде блок-схемы. А нам удобнее будет для начала записать функцию в виде формул:
Ниже приведено описание алгоритма в неформальной словесной форме. Этот способ мы всячески рекомендуем, потому что только после того, как задача четко описана на естественном языке, ее можно успешно записать на языке программирования. Для такой простой задачи, как рассматриваемая, это, быть может, и не имеет смысла, но вы ведь не собираетесь всю жизнь писать только элементарные программы!
1. Ввести значение аргумента х. 2. Определить, какому интервалу из области определения функции оно принадлежит. 3. Вычислить значение функции у по соответствующей формуле. 4. Вывести значение у.
Детализировать этот алгоритм уже практически некуда, поэтому сразу же смело напишем первый вариант программы:
Тестовые примеры для этой программы должны включать по крайней мере по одному значению аргумента из каждого интервала, а для проверки граничных условий - еще и все точки перегиба (если это кажется вам излишним, попробуйте в последнем условии «забыть» знак =, а затем ввести значение х, равное 2).
Как видно из программы, с помощью последовательности условных операторов практически «один в один» записана математическая форма описания функции приведенная выше. Обратите внимание на запись условий, содержащих два сравнения.
Операции отношения (<, >, ==, ≤, ≥,! =) являются бинарными, то есть имеют два операнда, и формируют результат типа bool, равный true или false1. Поскольку необходимо, чтобы эти условия выполнялись одновременно, они объединены с помощью операции логического И (& &) — не путать с поразрядным И! Приоритет у операции И ниже, чем у операций отношения, поэтому заключать их в скобки не требуется.
Весьма распространенная ошибка начинающих — запись подобных условий в виде кальки с математической формулы, то есть как а< Ь< с. Синтаксической ошибки в этом выражении нет, поэтому компилятор не выдает каких-либо сообщений. Давайте посмотрим, что же происходит при вычислении. Операции отношения одного приоритета выполняются слева направо, поэтому сначала будет выполнена операция а< Ь и сформирован результат в виде true или false. Следующая операция будет выглядеть как true< c или false< c. Для ее выполнения значения true и false преобразуются соответственно в единицу и ноль того же типа, что и с, и формируется результат, смысл которого вряд ли соответствует ожиданиям.
При работе приведенной выше программы всегда выполняются один за другим все пять условных операторов, при этом истинным оказывается только одно условное выражение и, соответственно, присваивание значения переменной у выполняется один раз. Запишем условные операторы так, чтобы уменьшить количество проверок:
Проверка на принадлежность аргумента очередному интервалу выполняется только в том случае, если х не входит в предыдущий интервал. Программа получилась более компактной, более эффективной, но, возможно, менее наглядной. В отличие от предыдущей версии, порядок следования условных операторов имеет здесь важное значение. Рассмотрим еще один вариант:
Запись фрагмента стала еще короче, но появились два недостатка: значение функции вычисляется многократно (от двух до пяти раз в зависимости от интервала, которому принадлежит х), значит, увеличилось время выполнения, а главное - программа потеряла универсальность, то есть таким способом можно вычислить не всякую функцию. Для того чтобы в этом убедиться, попробуйте заменить y=x на, к примеру, фрагмент окружности y=sqrt(1-x*x) и ввести значение х, большее 11 это приведет к ошибке в программе, связанной с вычислением квадратного корня из отрицательной величины.
Какой же вариант лучше? Для решения данной задачи разница между ними несущественна, но наша цель состоит в том, чтобы на простых примерах продемонстрировать общие принципы, следование которым позволит вам впоследствии создавать надежные и красивые программы.
СОВЕТ В современной иерархии критериев качества программы на первом месте стоят ее надежность, простота поддержки и модификации, а эффективность и компактность отходят на второй план. Поэтому в общем случае, если нет специальных требований к быстродействию, наиболее наглядный вариант предпочтительнее.
Нам кажется, что наиболее наглядным является самый первый вариант программы, поскольку по нему проще проследить логику ее работы. В заключение приведем вариант с использованием функций ввода-вывода в стиле С:
|